计算几何杂题选讲
A : LOJ2401 Dragon 2
如果暴力枚举每一条攻击的龙,那么有贡献的被攻击的龙的位置是这样的:(\(A\)为攻击的龙,\(CD\)为道路)
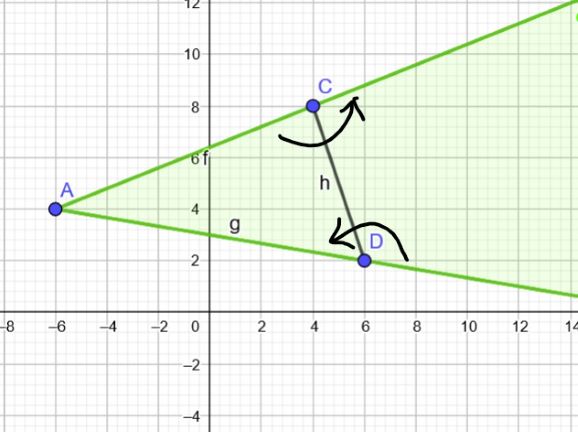
如果暴力枚举每一条被攻击的龙,那么有贡献的攻击的龙的位置是这样的: (\(B\)为被攻击的龙,\(CD\)为道路)
发现两种情况都可以看作分别以\(C,D\)两点为中心的一段(或两段)极角序区间的交
那么就可以用二维数点在 \(min(|A|,|B|)\log n\) 的复杂度内求出答案
因为题目保证询问不重复,所以复杂度为 \(O(n \sqrt n \log n)\)
(卡精度,注意 \(\pi\) 值的精度+全部使用 \(long\) \(double\) )
(upd: 也可以全用整数然后叉积来判断,细节较多。。。)
B : LOJ2549 【JSOI2018】 战争
思路巧妙的一道题
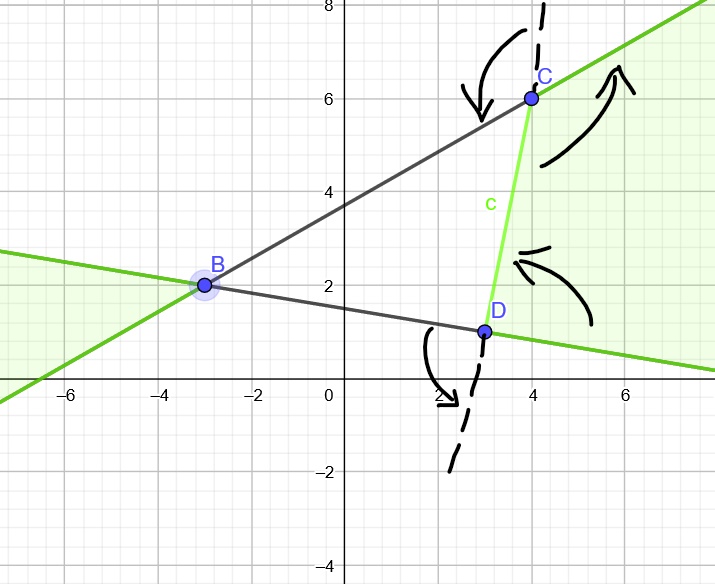
将凸包看作一个向量集
如果相交的话,从相交的多边形中选择一个向量\(\vec b\),找出该向量移动前对应的向量\(\vec a\),设移动向量为\(\vec w\)
则满足\(\vec a + \vec w = \vec b\) , 移项得\(\vec w = \vec b - \vec a\)
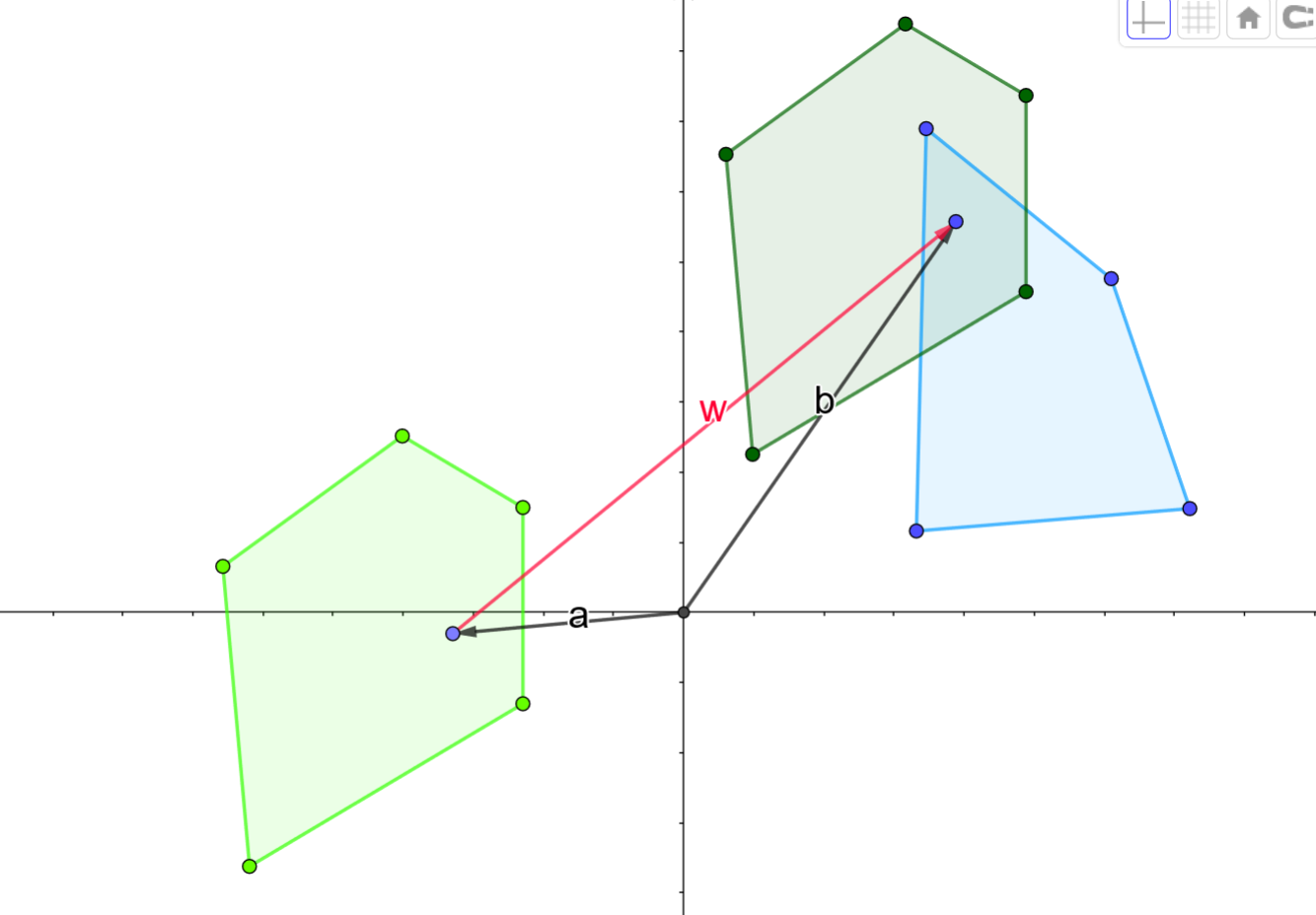
故原问题转化为:凸包 \(A'\) 与凸包 \(A\) 关于原点中心对称,求点 \(w\) 是否在 \(A'\) 与 \(B\) 的闵可夫斯基和中
于是写一个闵可夫斯基和凸包的板子就行了
C : LOJ2329 【清华集训2017】我的生命已如风中残烛
暴力模拟复杂度炸了,但发现实际模拟过程中其实一直在绕环
考虑如果发现绕出了环那么就直接计算绕多少圈
因为每次绕圈至少会减少一半的长度,所以复杂度就对了
不过直接这样做听说时间很卡
再预处理一个 \(nxt_{x}{pre}\) 表示当绳子足够长时,从 \(pre\) 绕到 \(x\) 后下一个会绕到那个点
同时对于每个点,将其他点按照极角序排的顺序都存下来
这样就可以优化掉暴力找下一个的复杂度,就没问题了
(upd:听说这样复杂度算下来还是很卡,但其实跑到蛮快的)
复杂度\(O(T*(n^3+n^2 m \log L))\) (超级小常数)
D : CF1326G Spiderweb Trees
观察到n不大,考虑暴力DP
设\(f_x\)表示x子树的划分方案数,那么\(Ans=f[1]\)
考虑\(f[x]\)如何求
设包含\(x\)的连通块为\(S\)
1: \(|S|=1\) \(\prod\limits_{y \in son_x}f_y\)
2: \(|S|=2\) \(\sum\limits_{y \in son_x}(\prod\limits_{v \in son_x \cap v \neq y}f_v)*(\prod\limits_{w \in son_y}f_w)\)
3: \(|S| \geq 3\)
此时, \(S\) 为一个一般的蜘蛛网树(叶子构成凸包)
考虑一个蜘蛛网树可以用所有叶子排序后表示
即 \((p_1,p_2,...,p_k)\) 表示叶子为这些点(逆时针排序),且包含所有路径上的点的连通子树
那么如果满足 \(\forall i , p_i \rightarrow p_{i+1}\) 路径上的点都在 \(\overrightarrow{p_i p_{i+1}}\) 的左侧,那么上述连通子树为蜘蛛网树,方案数为所有路径右侧儿子的 \(\prod f_p\)
找出所有合法路径,然后枚举起始边来 \(DP\)
复杂度为 \(O(n^4)\)
E :CF1195F Geometers Anonymous Club
miao~
首先考虑构造闵可夫斯基和凸包的算法过程
如果按照算法直径跑一遍,点数一定是n+m-1
但有些点只是在凸包的边上
发现只有斜率改变时在会新增顶点,而所有斜率全都会被遍历一般,于是答案就是区间不同斜率的数量
F :CF958E3 Guard Duty (hard)
e...,考虑分治
每次以最左下的点为极点,按照极角序排序,找到与极点配对,且能将点集分成两个合法子集的点,然后分治下去
(好像有点水了。。。)
G :CF77E Martian Food
两种方法:
1:笛卡尔定理+韦达定理

利用笛卡尔定理列出一元二次方程,发现两个根分别是 \(r_{i+1}\) 和 \(r_{i-1}\) ,用一下韦达定理递推即可
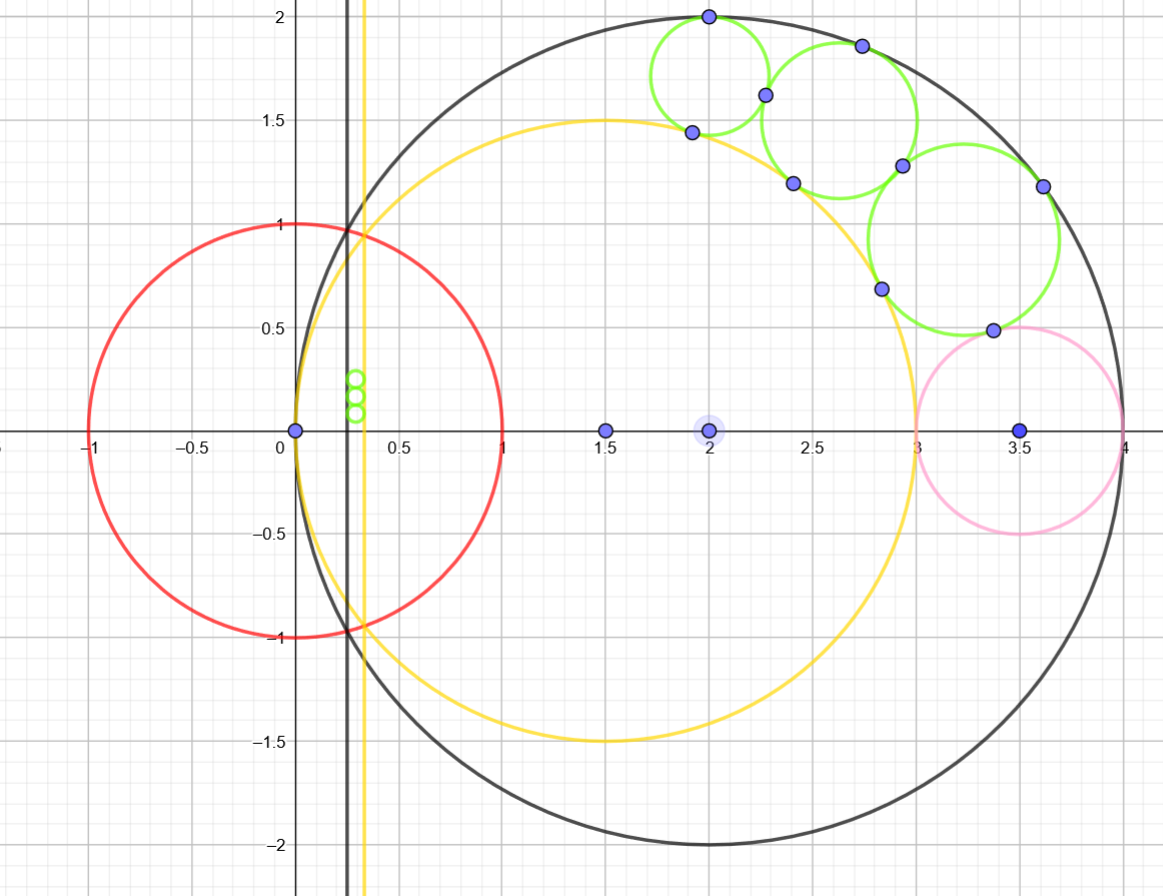
2:圆的反演
将以黑圆与黄圆的交点为原点,两圆心所在直线为x轴,建立坐标系
将两圆对单位圆反演,得到两条平行于y轴的直线,易知新圆反演后与两直线还有前一个圆相切
于是可以 \(O(1)\) 算出第k个圆反演后的位置,再反演回去即可
某大佬的博客:【科技】浅谈圆的反演
练习题:CF372E Drawing Circles is Fun
H :2017 ACM-ICPC world final A.Airport Construction
如果是凸包,显然可以旋转卡壳来求
考虑最长的线段一定在某两个顶点构成的直线上,否则可以调整使其更长
由于\(n \leq 200\),所以直接暴力枚举直线,然后暴力求直线被多边形截出的所有线段即可
复杂度 \(O(n^3)\)
I :LOJ2586 「APIO2018」选圆圈
miao~
三种做法:
1:乱搞
直接上 \(KD \_ tree\) ,发现卡飞了
旋转一下,就过了。。。
2: 仔细分析
发现求每个圆删除哪些不好求,考虑对每个圆求比它大的且与它相交的最先删去的圆
由于是主动删的,所以两两不交
又因为比该圆大,所以至少与 \(x+r,x-r,y+r,y-r\) 这四条直线中的一条相交
于是可以用扫描线来统计
复杂度 \(O(n \log n)\)
但是要对所有点都求答案怎么办?
\(CDQ\) 分治就行了
复杂度 \(O(n \log^2 n)\)
3:奇妙操作
考虑对平面分块,设当前最大圆的半径为 \(R\),将平面按照 \(2R\) 分块,那么只需要检查圆心所在格子以及相邻的 \(8\) 个格子
当半径小于 \(\frac{R}{2}\) 时重构即可
考虑分析复杂度:
首先显然最多重构 \(\log R\) 次,所以暴力重构的复杂度为 \(O(n \log R)\) 或 \(O(n \log n \log R)\)
考虑查询复杂度,有效查询的次数显然为 \(O(n)\)
考虑在一次分块下的无效查询次数,显然每个块内最多主动删除 \(2\) 个圆,而每个圆只会检索 \(9\) 个格子,即每个格子最多被检索 \(18\) 次
故每个圆每次分块被无效查询的次数为常数级别
所以总复杂度为 \(O(n \log R)\) 或 \(O(n \log n \log R)\)
J : UOJ242 破坏蛋糕
首先旋转平面,使第 \(n+1\) 条直线 "高稳鸡光" 落在y轴上
考虑每一段封闭的条件为过两端点的直线在左右两侧均和其他直线有交
我们考虑左侧如何计算,右侧同理
考虑一条直线会与在它上方的,且斜率大于它的直线有交
那么可以维护一个单调栈,每次用当前直线的斜率在上面二分,找到最靠上的相交的直线,那么这个区间就都满足条件
出题人很良心,限制掉了很多特殊情况
( upd:很凉心,卡精度,判断斜率相等要用旋转前的直线叉积来判,三角函数精度炸了:( )
鸣谢:(题目来源)
(题目部分找自大佬们刷杂题写的博客,要不还真找不到这么多题sto)


