csp-s模拟82

T1:
  考虑一个逆序对的贡献
  设\(f_i\)表示一个逆序对对长度为i的序列的贡献
  \(f_i = (\sum_{j=2}^n(^{n-2}_{j-2})f_j )/2^n\)
  最后的答案为：\((\sum_{i=1}^n (^i_2)(^i_2)(i-2)! / i! *f_i )/n\)
  将f的式子移一下项即可得到递推式，打个表后会发现当\(i>1\)时\(f_i=4/3\)
  将\(f_i=4/3\)带入答案的式子，化简即可。
 
T2:
  枚举分界点统计以i结尾的后缀个数\((f_i)\)和以i开头的前缀个数\((g_i)\)。
  \(ans = \sum_{i=1}^{n-1}f_i*g_{i+1}\)
  考虑如何快速统计
  对所有串和反串分别建出tire树，在每个节点统计该点到根的hash值,存到hash表里
  再求出tire树每个节点包含了多少前缀/后缀
  再预处理串\(S\)和\(S^R\)的hash值
  枚举分界点，二分找到最长前缀匹配和最长后缀匹配
  利用tire树上节点统计的信息即可快速求出f和g
 
T3:
  发现当皇后的个数大于5之后，合法的方案就只有将她们排成一排
  分别计算一下横竖斜三种情况即可
  小于等于5时，发现并没有一个通用的公式，那就分5种情况讨论
  1和2比较简单，就不赘述了
  3（3种）：

  4（4种）：

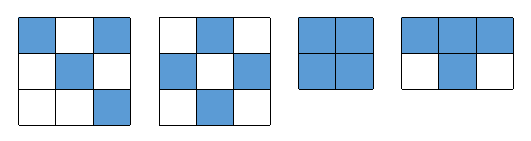
  5（2种）:

  推推式子就好了