椭圆曲线算法的基本原理及实现
1、基本概念
1)椭圆曲线方程的一般形式:y^2 = x^3 + a*x + b,其中要求满足不等式 4*a^3 + 27*b^2 ≠ 0
例如:y^2 = x^3 + x + 1 mod 23
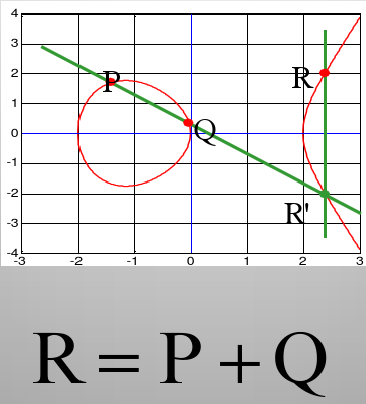
2)椭圆曲线上的点的加法公式(适用于 P ≠ Q 的情况):设 P = (x1, y1),Q = (x2, y2),P + Q = R = (x3, y3),t = (y2-y1)/(x2-x1),x3 = t^2 - x1 - x2,y3 = t*(x1 - x3) - y1
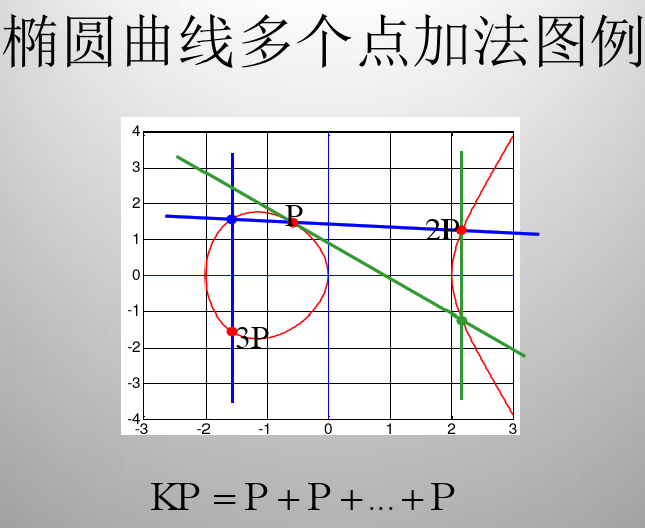
3)椭圆曲线上的点的加法公式(当上面的 P = Q 时):P + P = R = (x3, y3),t = (3*x1^2+a)/(2*y1),x3 = t^2 - x1 - x1,y3 = t*(x1 - x3) - y1

2、准备步骤
1)随机生成一个数 d 做私钥
2)选椭圆曲线上的一个点 P,计算 Q = d*P 做公钥
设 A 要加密 M 送给 B,B 的私钥为 d,公钥为 Q = d*P
3、加密过程
1)A 随机生成一个数 k
2)计算 k*P 和 k*Q
3)取 k*Q 的横坐标与 M 异或得到密文 C
4)A 发送 k*P 和密文 C 给 B
4、解密过程
1)B 用自己的私钥 d 计算 d*(k*P)
2)B 用 d*(k*P) 的横坐标与密文 C 异或得到 M
5、加密及解密的实现
1 import java.util.ArrayList; 2 import java.util.HashMap; 3 4 public class Main { 5 // 选用的椭圆曲线为 y^2 = x^3 + x + 1 mod 23 6 private static int a = 1, b = 1; 7 private static HashMap<Integer, Integer> myPoints = new HashMap<>(); 8 private static final int MAX = 255; 9 10 public static void main(String[] args) { 11 // 明文和密文数组的初始化 12 char[] myInfo = "1700802067GJQ".toCharArray(); 13 int[] i_mingwen = new int[myInfo.length]; 14 int[] miwen = new int[i_mingwen.length]; 15 char[] c_mingwen = new char[miwen.length]; 16 for (int i = 0; i < myInfo.length; i++) { 17 i_mingwen[i] = (int)myInfo[i]; 18 } 19 20 // 初始化椭圆曲线上的整数点 21 initPoints(); 22 23 // 显示椭圆曲线上的整数点 24 // showPoints(); 25 26 // 获取椭圆曲线上点的横坐标集合 27 Object[] objArr = myPoints.keySet().toArray(); 28 ArrayList<Integer> myList = new ArrayList<>(); 29 for (Object o: objArr) { 30 myList.add((Integer) o); 31 } 32 33 // 随机取椭圆曲线上一个点 34 int Px = myList.get((int)(Math.random()*myList.size())); 35 int Py = myPoints.get(Px); 36 MyPoint p = new MyPoint(Px, Py); 37 38 // 随机取一个 8bit 的数作为私钥 39 int d = (int)(Math.random()*MAX) + 1; 40 // 计算Q 41 MyPoint Q = new MyPoint(p); 42 myECC(Q, 1, d); 43 44 // 随机取一个 8bit 的数k 45 int k = (int)(Math.random()*MAX) + 1; 46 47 // 计算 k*P 和 k*Q 48 MyPoint kP = new MyPoint(p); 49 myECC(kP, 1, k); 50 MyPoint kQ = new MyPoint(Q); 51 myECC(kQ, 1, k); 52 53 // 加密 54 int kQx = kQ.getX(); 55 for (int i = 0; i < i_mingwen.length; i++) { 56 miwen[i] = i_mingwen[i] ^ kQx; 57 } 58 59 // 计算d*(k*P) 60 MyPoint dkP = new MyPoint(kP); 61 myECC(dkP, 1, d); 62 63 // 解密 64 int dkPx = dkP.getX(); 65 for (int i = 0; i < miwen.length; i++) { 66 c_mingwen[i] = (char) (miwen[i] ^ dkPx); 67 } 68 69 // 输出对密文解密后的明文 70 System.out.println(c_mingwen); 71 } 72 73 public static void initPoints() { 74 double y; 75 for (int i = 0; i < 23; i++) { 76 y = Math.sqrt((Math.pow(i, 3) + i + 1)%23); 77 if (y == (int)y) myPoints.put(i, (int)y); 78 } 79 } 80 81 public static void myECC(MyPoint p, int i, int d){ 82 if (i < d) { 83 int t = (3*(int)Math.pow(p.getX(), 2)+a)/(2*p.getY()); 84 int x = (int)(Math.pow(t, 2)) - 2*p.getX(); 85 int y = t*(p.getX() - x) - p.getY(); 86 p.setX(x); 87 p.setY(y); 88 myECC(p, i+1, d); 89 } 90 } 91 92 public static void showPoints() { 93 myPoints.forEach((k, v) -> { 94 System.out.println("key: " + k + ", " + "value: " + v); 95 }); 96 } 97 } 98 99 class MyPoint { 100 private int x; 101 private int y; 102 MyPoint() {} 103 MyPoint(int x, int y) { 104 this.x = x; 105 this.y = y; 106 } 107 MyPoint(MyPoint P) { 108 this.x = P.getX(); 109 this.y = P.getY(); 110 } 111 public void setX(int x) { 112 this.x = x; 113 } 114 public void setY(int y) { 115 this.y = y; 116 } 117 public int getX() { 118 return this.x; 119 } 120 public int getY() { 121 return this.y; 122 } 123 }
6、注解:
1)A 用 k*P 与 B 用 d*(k*P) = k*(d*P) = k*Q
2)经过两次异或得到原文(明文)
参考文档:
https://wenku.baidu.com/view/ff42b6610b1c59eef8c7b477.html
遇到的疑问(已解决):
1)Objct[] 数组不能直接转换为 ArrayList。
2)函数不能返回两个值,可以将要返回的值放入对象中,在函数中改变对象的值。
遇到的疑问(未解决):
1)P点的横纵坐标对后续的计算并无影响,即可以不取椭圆曲线上的点。



