Gitea 1.18 版 Markdown 渲染器引入 KaTeX 模块，支持在前端页面实时渲染数学公式
我们在 Gitea 1.18 版的 Markdown 渲染器中引入了 KaTeX 模块，这使得 Gitea 前端界面具备了渲染数学公式的能力，你可以在文本编辑器中混合使用 TeX 语法，在线分享你的数学公式！
关于数学公式
Gitea 在前端实现的数学渲染功能基于的 KaTeX：一个轻量、开源、基于 JavaScript 的 TeX 渲染引擎。KaTeX 支持的数学符号是 TeX 的子集，更多信息请参考支持列表。
Gitea 1.18 的默认文本渲染器已经支持数学公式渲染功能。你可以在工单、合并请求、百科、评论和任意 Markdown 文件中编写类似 TeX 标记语法的数学公式。
全局功能开关
Gitea 内置的 Markdown 渲染器默认启用了数学渲染功能，这项功能也支持手动关闭。
要编辑配置，请打开 Gitea 的配置文件 custom/conf/app.ini，找到 [markdown] 栏目，并修改 ENABLE_MATH（如果没有，手动输入即可），示例如下：
[markdown]
;; Enables math inline and block detection
ENABLE_MATH = true
然后，请重新启动 Gitea 服务使得配置文件载入生效。
在段落中内联公式
要在段落中包含内联的数学公式，请使用一对美元符号 $...$ 或者 \(...\)包裹公式。示例如下：
This sentence uses `$` delimiters to show math inline: $\sqrt{3x-1}+(1+x)^2$
以代码块的形式插入公式
如果你想要像插入程序代码块那样插入数学公式，请务必从新的一行开始，使用一对双美元符号 $$...$$ 或者 \[...\] 包裹公式，示例如下：
**The Cauchy-Schwarz Inequality**
$$\left( \sum_{k=1}^n a_k b_k \right)^2 \leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right)$$
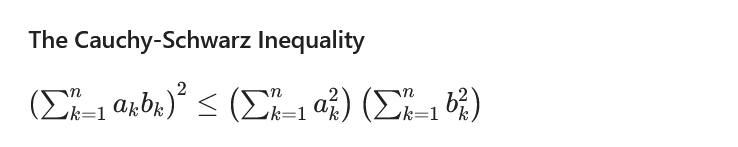
或者，可以使用 Markdown 语法 ```math ``` 包裹数学公式块。使用此语法可以代替 $$...$$。
**Here is some math!**
```math
\sqrt{3}
```
在数学公式中书写美元符号
如要将公式中的美元符号$作为字符显示，请使用转义字符 \$ 以确保字符被正确解析。
- 在数学公式中，在
$字符之前添加\符号。
This expression uses `\$` to display a dollar sign: $\sqrt{\$4}$
- 使用
\(...\)代替$...$; 使用\[...\]代替$$...$$
To split $100 in half, we calculate \(100/2\)
示例
在 Markdown 文本编辑器中混合使用 TeX 语法编写公式。
渲染之前
where \(\tilde{\lambda}\in (\Z^{2n}_+)^{\mathrm{Hom}(F, \overline{\mathbb{Q}}_p)}\) is the highest weight
of the representation \(\iota^{-1}(\xi\otimes \xi)^\vee\) of \((\mathrm{Res}{F/\mathbb{Q}}\mathrm{GL}{2n}){\overline{\mathbb{Q}}_p}\).[^1]
* If \(F_0\subset F\) is an imaginary quadratic field and \(\ell\) is a prime
which splits in \(F_0\) (including possibly \(\ell=p\)), then for each prime \(v\mid \ell\) of \(F\) lying above
a prime \(\bar{v}\) of \(F^+\), there is an isomorphism
\[
\mathrm{WD}\left(r_{\iota}(\pi)|{G{F_v}}\right)^{F-ss} \simeq \mathrm{rec}^T_{F_v}
(\pi_{\bar{v}}\circ \iota_v).
\]
\[ a < b > c \]
\[x=5\]
[^1]: For each \(\overline{\tau}:F^+\to \mathbb{C}\), \(\xi\) gives a representation of \(\mathrm{tG}{\overline{\tau}}\) and hence for \(\tau,\tau c\) extending \(\overline{\tau}\) to \(F\) we have a represententation \(\xi\otimes\xi\) of \(\mathrm{tG}_{\overline{\tau}}\times \mathrm{tG}_{\overline{\tau}} = (\mathrm{GL}_{2n,F}){\tau} \times (\mathrm{GL}{2n,F}){\tau c}\).
Note that \(r_{\iota}^{\vee,c}(1-2n)\cong r_{\iota}(\pi)\) so \(\mathrm{HT}_{\tau}(r_{\iota}(\pi))\) and \(\mathrm{HT}_{\tau c}(r_{\iota}(\pi))\) can be read off from each other.
渲染之后
