SPOJ:[DIVCNT3]Counting Divisors

 

 

 

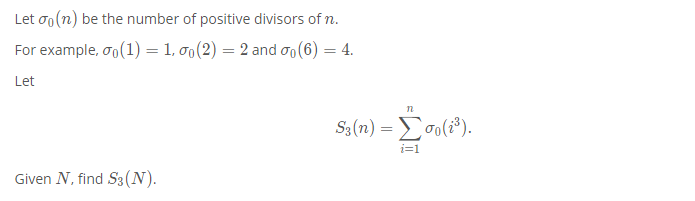
题目大意：求1~N的每个数因子数的立方和。

题解：由于N过大，我们不能直接通过线性筛求解。我们可以采用洲阁筛。

洲阁筛的式子可以写成：

 

对于F(1~√n)，可以直接线性筛求解。

 

对于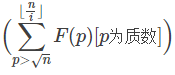，我们进行以下DP：

g[i][j]为1~j中，与前i个质数互质的数的F值之和。

dp过程中，有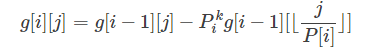

如果p[i]>j，则g[i][j]=F(1)；

如果p[i]*p[i]>j>=p[i]，则g[i][j]=g[i-1][j]-p[i]^k*F(1)=g[d][j]-(p[d+1]^k~p[i]^k)*F(1)，其中p[d]为最大的p[d]*p[d]<=j的质数；

如果j>=p[i]*p[i]，我们老老实实调用式子。

 

对于，我们用类似的方式DP：

f[i][j]为1~j中，只以第i个到第m个质数为质因子的数的F值之和（m为√N以内质数个数）。

类似的，dp过程中，有

如果p[i]>j，则f[i][j]=F(1)；

如果p[i]*p[i]>j>=p[i]，则f[i][j]=f[i+1][j]+F(p[i])*F(1)=F(1)+F(p[i]~p[e])*F(1)，其中p[e]为最大的p[e]<=j的质数；

如果j>=p[i]*p[i]，我们老老实实调用式子。

 

代码：

#include<bits/stdc++.h>
using namespace std;
long long block,n,lb[2000005],dp[2000005],zs[2000005],ans[2000005],ans2;
bool bo[2000005],bo2[2000005];
int dp2[2000005],dp3[2000005],m,mm,tot,j,bo3[2000005],tt;
void xxs(int n)
{
    ans[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(bo[i]==0){ mm++; zs[mm]=i; ans[i]=4; bo2[i]=1; bo3[i]=4; }
        for(int j=1;j<=mm;j++)
        if(zs[j]*i>n)break;else
        if(i%zs[j]==0)
        {
            if(bo2[i]==1)bo2[i*zs[j]]=1; bo3[i*zs[j]]=bo3[i]+3; ans[i*zs[j]]=ans[i]/bo3[i]*(bo3[i]+3);
            bo[i*zs[j]]=1; break;
        }else { ans[i*zs[j]]=ans[i]*4; bo[i*zs[j]]=1; bo3[i*zs[j]]=4; }
    }
}
int dy(long long x){ if(x<=block)return x;else return tot-n/x+1; }
long long get(int i,int j)
{
    if(dp2[j]==i)return dp[j];else 
    if(lb[j]<zs[i]){ if(j>0)return 1; return 0; } 
    return dp[j]-i+dp2[j];
}
long long get2(int i,int j)
{
    if(dp2[j]==i)return dp[j];else 
    if(lb[j]<zs[i])return 1; 
    return (dp3[j]-i+1)*4+1;
}
int main()
{
    scanf("%d",&tt); xxs(500000);
    for(int ii=1;ii<=tt;ii++)
    {
        scanf("%lld",&n); block=(int)sqrt(n); ans2=0;
        for(m=1;m<=mm;m++)if(zs[m]>block)break; m--; tot=0;
        for(int i=1;i<=block;i++){ lb[++tot]=i; if(1ll*i*i<n)lb[++tot]=n/i; }
        sort(lb+1,lb+tot+1);
        for(int i=1;i<=tot;i++)dp[i]=lb[i],dp2[i]=0;
        for(int i=1;i<=m;i++)
        {
            for(int j=tot;j>=1;j--)
            {
                if(lb[j]<zs[i]*zs[i])break; dp2[j]=i;
                dp[j]=dp[j]-get(i-1,dy(lb[j]/zs[i]));
            }
        }
        for(int i=1;i<=block;i++)
        ans2=ans2+ans[i]*(get(m,tot-i+1)-1)*4;
        j=1; 
        for(int i=1;i<=tot;i++)
        {
            dp[i]=1; dp2[i]=m+1;
            while((j<=m)and(zs[j]<=lb[i]))j++; dp3[i]=j-1;
        }
        for(int i=m;i>=1;i--)
        {
            for(int j=tot;j>=1;j--)
            {
                if(lb[j]<zs[i]*zs[i])break; dp[j]=get2(i+1,j); dp2[j]=i;
                long long t=j,l=1; 
                while(lb[t]>=zs[i])
                {
                    t=dy(lb[t]/zs[i]); l+=3;
                    dp[j]=dp[j]+l*get2(i+1,t);
                }
            }
        }
        ans2=ans2+get2(1,tot);
        printf("%lld\n",ans2);
    }
}