TopCoder[SRM587 DIV 1]:TriangleXor(550)

Problem Statement

You are given an int W. There is a rectangle in the XY-plane with corners at (0, 0), (0, 1), (W, 0), and (W, 1). Let T[x] be the triangle with vertices at (0, 1), (W, 1) and (x, 0). (All points that lie inside the triangle are a part of T[x] as well.)

The objective in this problem is to calculate the area of the region (T[0] xor T[1] xor ... xor T[W]). (See Notes for a formal definition.) The figures below show the region (T[0] xor T[1] xor ... xor T[W]) for W=1,2,3,4,5,6.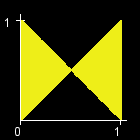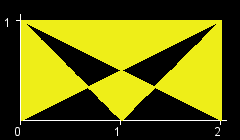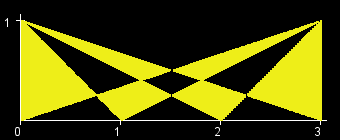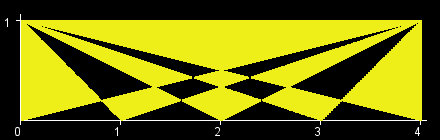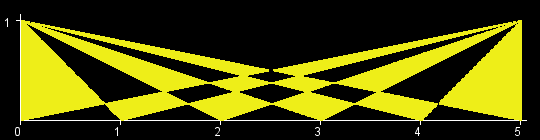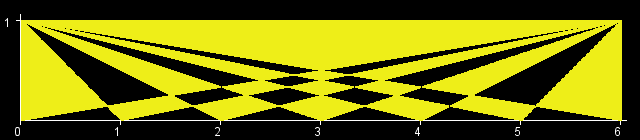

   

 

 

Return the integer part of the area of the region.

Definition

Class:	TriangleXor
Method:	theArea
Parameters:	int
Returns:	int
Method signature:	int theArea(int W)
(be sure your method is public)

Limits

Time limit (s):	2.000
Memory limit (MB):	64

Notes

-

For sets of points A and B in the XY-plane, the set (A xor B) is defined as the set of all points that lie in exactly one of the sets A and B (i.e., points that belong to the union of A and B but don't belong to their intersection).

-

If the exact area is A, the correct return value is floor(A), not round(A). In words: you should return the largest integer that is less than or equal to the exact area.

-

The format of the return value was chosen to help you in case of small precision errors. The constraints guarantee that computing the correct area with absolute error less than 0.01 is sufficient to determine the correct return value. The author's solution is significantly more precise than that.

Constraints

-

W will be between 1 and 70,000, inclusive.

-

The difference between the exact area of the region and the nearest integer will be greater than 0.01.

Examples

0)

1

Returns: 0

The exact area is 0.5.

1)

2

Returns: 1

The area is approximately 1.33333.

2)

3

Returns: 1

The exact area is 1.35.

3)

4

Returns: 2

The area is approximately 2.62857. Note that the correct answer is 2, not 3.

4)

5

Returns: 2

The area is approximately 2.13294.

5)

12345

Returns: 4629

题意：给你一个1*n的矩形，按图中方法划线、涂色，问多大面积涂为黄色。

 

题解：

根据题目中的图，可以用两条对角线把涂色区域分为四个部分。

对于上方部分，若n为偶数，全为黄色；若为奇数，全为黑色。

对于左右部分，通过三角形的相似求出各个等高三角形的底之和与对角线长度的比例，计算面积。

对于下方部分，同样通过相似求出各组等高四边形的底之和与高，计算面积。

 

代码：

class JumpFurther
{
    public:
    int furthest(int N, int badStep)
    {
        //$CARETPOSITION$
        int tot=0,x=0;
        for(int i=1;i<=N;i++)
        {
            tot=tot+i; if(tot==badStep)x--;
        }
        return tot+x;
    }
};