数组与广义表

数组与广义表

No.1数组的定义

数组

  1. 数组：按一定格式排列起来的，具有相同类型的数据元素集合。
  2. 一般都是采用顺序存储结构来表示数组。
  3. 数组可以是多维的，但存储数据元素的内存单元地址是一维的，因此，在存储数组结构之前，需要解决将多维关系映射到一维关系的问题。
  4. 结论：线性表结构是数组结构的一个特例，而数组结构又是线性表结构的扩展。
  5. 特点：结构固定——定义后，维数和维界不再改变。
  6. n维数组：若 n-1 维数组中的元素又是一个一维数组结构，则称为n维数组。
typedef int ElemType; 
typedef struct{
    ElemType *base; /* 数组元素基址，由InitArray分配 */
    int dim;        /* 数组维数 */
    int *bounds;    /* 数组维界基址，由InitArray分配 */
    int *constants; /* 数组映象函数常量基址，由InitArray分配 */
} Array;

一、一维数组

  1. 一维数组：若线性表中的数据元素为非结构的简单元素，则称为一维数组。
  2. 一维数组的逻辑结构：
    1. 线性结构（定长的线性表）
  3. 声明格式：数据类型 变量名称[长度]
  4. 各数组元素大小相同，且在物理上连续存放。

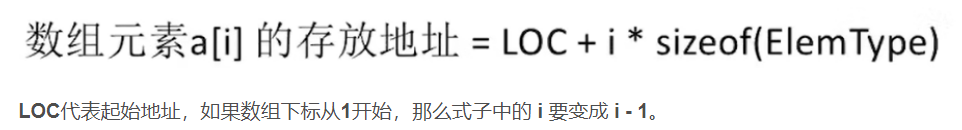
二、二维数组

  1. 二维数组：若一维数组中的元素又是一个一维数组结构，则称为二维数组。

  2. 二维数组的逻辑结构：

    1. 非线性结构：每一个数据元素即在一个行表中，又在一个列表中。
    2. 线性结构（定长的线性表）：该线性表的每个数据元素也是一个定长的线性表。

  3. 声明格式：数据类型 变量名称[行数] [列数]

  4. 其内存表示分为两种不同的存储策略，一种是行优先存储，一种是列优先存储：

    1. 行优先存储，即一行一行的存：

  1. 列优先存储，即一列一列的存：

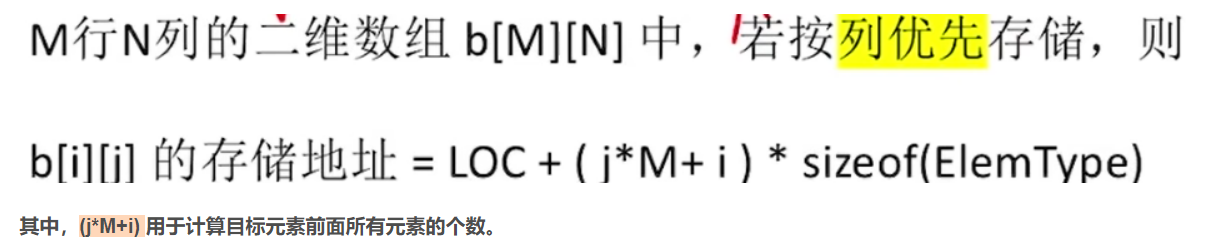
三、三维数组

  • 三维数组：若二维数组中的元素又是一个一维数组结构，则称为三维数组。

No.2特殊矩阵压缩存储

  • 矩阵：一个由 m × n 个元素排成的m行n列的表。

  • 矩阵的常规存储：将矩阵描述为一个二维数组。

  • 矩阵的常规存储的特点：

    1. 可以对其元素进行随机存取。
    2. 矩阵运算非常简单。
    3. 存储的密度为1。

  • 行优先与列优先

image-20230524010458580

  • 映射：数组的下标0与1与矩阵Aᵢ Aⱼ的元素下标i和j的关系就是所谓的映射

  • 矩阵的压缩存储：在一个矩阵中，若多个数据的值相同，为了节省内存空间，则只分配一个元素值的空间，且零元素不占存储空间。

  • 公式：

    1. 矩阵非零元素A(i)(j)在一维数组B中求对应下标
      Loc[i,j]=Loc[1,1]+(a(i)(j)前面的非零元素个数）） --> Loc[1,1]代表的是首地址
    2. 矩阵非零元素a(i)(j)在一维数组B中地址(size是单个元素的字节大小）
      Loc[A(i)(j)]=Loc[A(1,1)]+(a(i)(j)前面的非零元素个数))∗size

  • 注意点：由于通常Loc[1,1]即A(1)(1)在一维数组B中下标是0（下面给的公式也是按照B数组下标从0开始），所以0就被省略，没有写出来

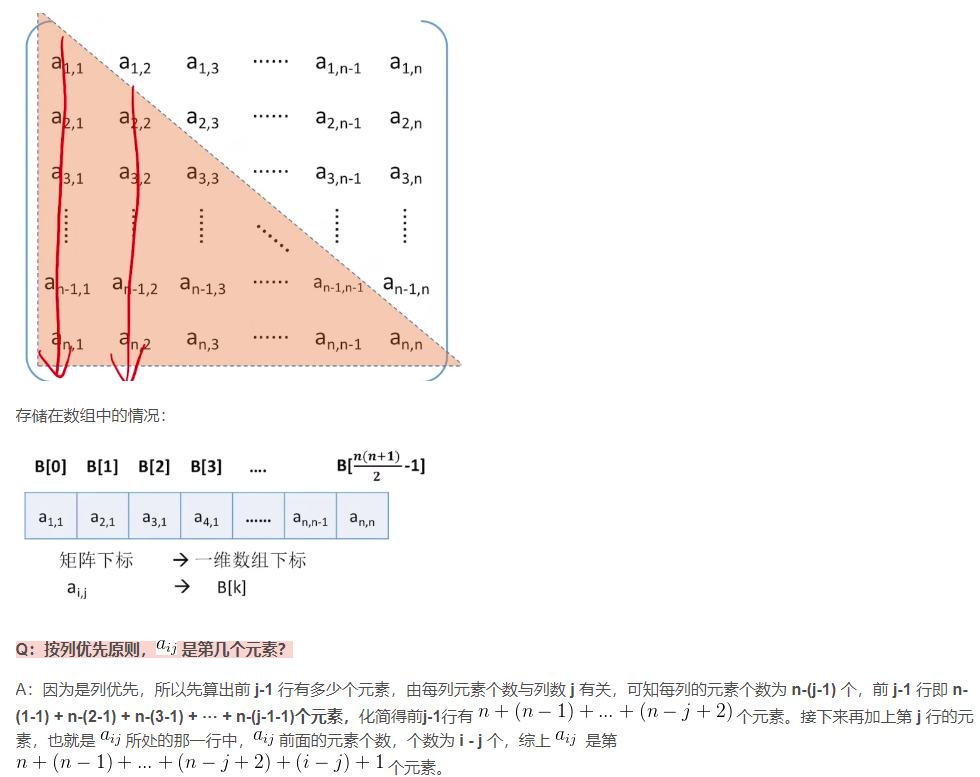
一、对称矩阵

image-20230523221357779

  • 对称矩阵是指元素以主对角线为对称轴对应相等的n阶矩阵，即aᵢⱼ=aⱼᵢ （ 注意，n阶的意思是行数和列数相同。）

  • 只存储下（或者上）三角（包括主对角线）的数据元素。

  • 共占用 n(n+1) / 2 个元素空间。

  • 按行优先原则将各个元素存入一维数组中：

  • *按列优先原则将各个元素存入一维数组中：

  • 注意点：

二、三角矩阵

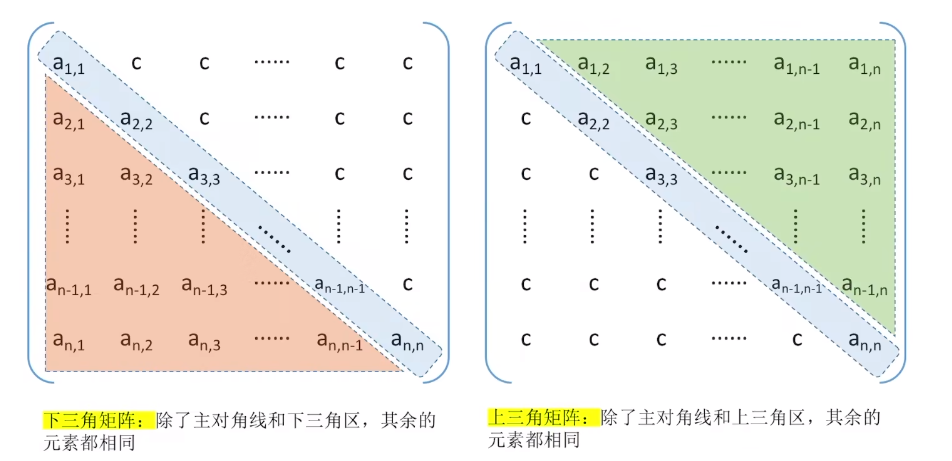
  • 三角矩阵分为下三角矩阵和上三角矩阵。
  • 共占用 n(n+1) / 2 + 1个元素空间。（多出来的一个空间用于存储常数C）
  • 对角线以下（或者以上）的数据元素（不包括对角线）全部为常数C。
  • 按照行优先或者列优先原则，把不是常量的区域的数据放到一维数组中，并仅在数组最后一个位置(下图c处)存储常量。

  • 下三角矩阵

  • 上三角矩阵

  • 若要使用列优先，则相互使用双方的相反形式（i与j对调）

三、对角矩阵

  • 在 n 阶矩阵中，所有非零元素都集中在以主对角线为中心的带状区域中，区域外的值全为0。

  • 常见的有：三对角矩阵、五对角矩阵、七对角矩阵。

  • 非零a(i)(j)特点；

    1. i = 1(第一行，只有两个元素）：j = 1, 2
    2. 1 < i < n（中间行，每行有三个元素，j有三个取值）：j = i - 1, i , i +1
    3. i = n (最后一行，只有两个元素）： j = n-1, n

  • 压缩方法：

    1. 确定存储该矩阵所需的一维存储空间（即一维数组B）的空间大小
      每一行假设都有3个元素，但是由于第一行和最后一行只有两个，所以一维数组的容量为：3n - 2
    2. 确定非零元素a(i)(j)在一维空间的下标（地址)
      这里假设一维数组B的下标是从0开始，即首元素A[1] [1]在B数组的下标是0，由此得出A[i] [j]在B数组的下标为它前面的元素个数

  • 非零元素a(i)(j)在一维空间的下标位置：前 i - 1 行非零元素个数 + 第i行中非零元素个数 = 3（i-1）-1 + j - i + 1

  • 前 i - 1 行非零元素个数：3（i-1）-1

  • 第i行中非零元素个数: j - i + 1

    1. j - i = - 1 (j < i)
    2. j - i = 0 (j = i)
    3. j - i = 1 (j > i)

由此得到：A(i)(j)在B数组中的下标为（其中Loc(1)(1) = 0 Loc[i,j]=Loc[1,1]+(2(i−1)+j−1）

四、稀疏矩阵

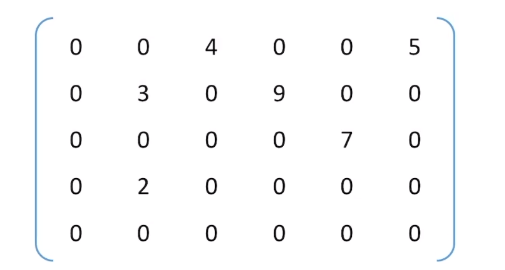
  • 非零元素的个数远远少于矩阵元素的个数（一般小于5%）
  • 非零元素个数 / 元素总个数 ≤ 0.05 则满足条件。
  • 稀疏矩阵有两种压缩存储方式：
    1. 三元组法
    2. 十字链表法
1.三元组
  • 以三元组的形式进行顺序存储。
  • 就是给每个非零元素在存储自身的值的基础上再加两个域。
    1. 行域：存储这个非零元素在原来的的矩阵中所占的行号。
    2. 列域：存储这个非零元素在原来的矩阵中所占的列号。
    3. 值域：存储原来的非零元素的值。

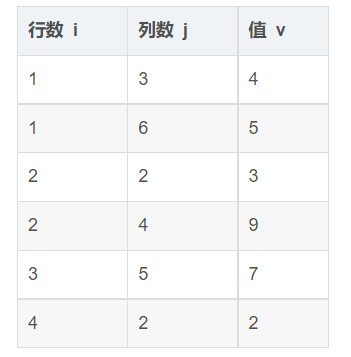
#define MAXSIZE 1000	//非零元素个数最多为1000

//三元组的定义，用于存储一个非零元素
typedef struct{
	int row,col;	//存储该非零元素的行和列
	ElementType e;	//存储该非零元素的值
} Triple;

//三元组表的定义
typedef struct{
	Triple data[MAXSIZE + 1];	//非零元素的三元组表。data[0]未用
	int m, n, len;	//原来矩阵的行数、列数、非零元素的个数
}TSMatrix;
2.十字链表

  • 以十字链表法进行链式存储

  • 每一个非零元素节点，不仅有这3个域：（row , col , value).还增加了两个链域：

    1. right:链接同一行中的下一个非零元素
    2. down:链接同一列中的下一个非零元素

  • 在十字链表中，同一行的的非零元素由于right指针链接成一个单链表。同一列的非零元素通过down指针链接成一个单链表。
    所以某一个非零元素，既会属于某一行，也会属于某一列，行和列在这一点相交，像一个十字路口，所以这种方法根据这种形象的感觉，命名为：十字链表法。
    同时，还需要设两个一维数组：

    1. 一个负责存储行的单链表的头指针
    2. 一个负责存储列的单链表的头指针

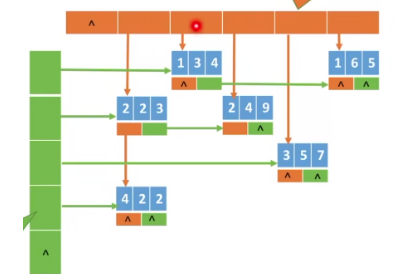
typedef struct OLNode{
	int row, col;	//非零元素的行号和列号
	ElementType value;   //非零元素的值
	struct OLNode *right, *down;	//非零元素所在行链、列链的后继指针域
}OLNode; * OLink;

typedef struct{
	OLink * row_head, *col_head;	//两个辅助一维数组，存储行链表、列链表的头节点
	//CrossList.row_head = (OLink *)malloc ( (m+1) ,sizeof (OLink));
	int m, n, len;	//存储原矩阵的行数、列数、非零元素个数
}CrossList;

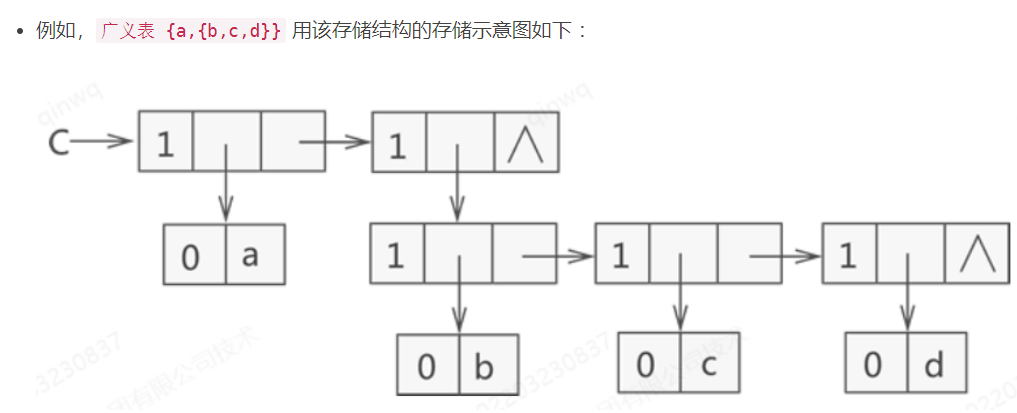
No.3广义表的定义

  • 广义表，又称列表，也是一种线性存储结构，既可以存储不可再分的元素，也可以存储广义表，记作：LS = (a1,a2,…,an)，其中，LS 代表广义表的名称，an 表示广义表存储的数据，广义表中每个 ai 既可以代表单个元素，也可以代表另一个广义表。

  • 广义表中存储的单个元素称为 "原子"，而存储的广义表称为 "子表"。
    例如 ：广义表 LS = {1,{1,2,3}}，则此广义表的构成 ：广义表 LS 存储了一个原子 1 和子表 {1,2,3}。

  • 广义表存储数据的一些常用形式：

    1. A = ()：A 表示一个广义表，只不过表是空的。
    2. B = (e)：广义表 B 中只有一个原子 e。
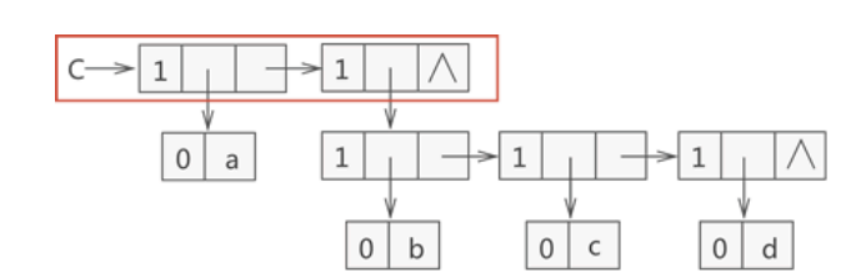
    3. C = (a,(b,c,d)) ：广义表 C 中有两个元素，原子 a 和子表 (b,c,d)。
    4. D = (A,B,C)：广义表 D 中存有 3 个子表，分别是A、B和C。这种表示方式等同于 D = ((),(e),(b,c,d)) 。
    5. E = (a,E)：广义表 E 中有两个元素，原子 a 和它本身。这是一个递归广义表，等同于：E = (a,(a,(a,…)))。

  • 当广义表不是空表时，称第一个数据（原子或子表）为"表头"，剩下的数据构成的新广义表为"表尾"。

  • 除非广义表为空表，否则广义表一定具有表头和表尾，且广义表的表尾一定是一个广义表。

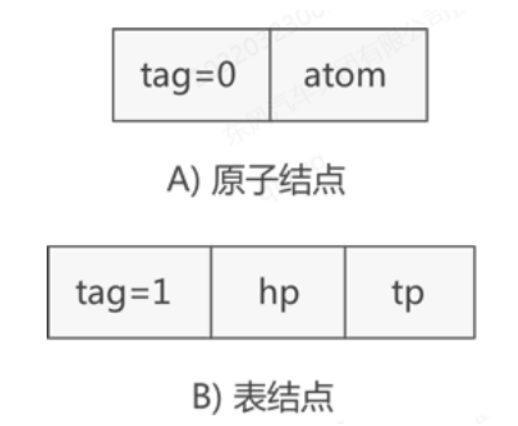
typedef char AtomType;
typedef enum {
	ATOM,    // ATOM == 0：原子
	LIST     // LIST == 1：子表
}ElemTag;

typedef struct GLNode {
	ElemTag tag;        // 公共部分，用于区分原子结点和子表结点
	union {             // 原子结点和子表结点的联合部分
		AtomType atom;   // atom是原子结点的值域
		struct {           // ptr是子表结点的值、指针域
			struct GLNode* hp;   // 表头
			struct GLNode* tp;   // 表尾
		}ptr;
	};
}GLNode, * GList;

一、广义表的深度

  • 广义表的深度，可以通过观察该表中所包含括号的层数间接得到，如下示例，该广义表的深度为2。
  • 注意点：递归广义表的深度是无穷大！！！

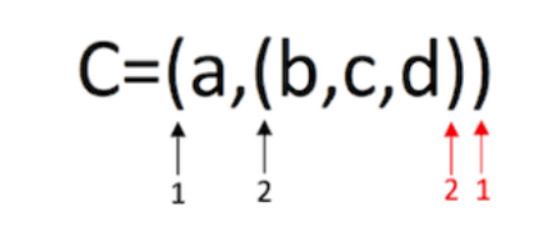
//求广义表L的深度
int GListDepth(GList L) {
	if (L == NULL)         // 空表深度=1
		return 1;
	else if (L->tag == ATOM) // 原子深度=0
		return 0;
    else {
        int maxDepth = 0;
        GList p = L->ptr.hp;
        while (p != NULL) {
            int depth = GListDepth(p);
            if (depth > maxDepth)
                maxDepth = depth;
            p = p->ptr.tp;
        }
        return maxDepth + 1;
    }
}

二、广义表的长度

  • 广义表的长度，指的是广义表中所包含的数据元素的个数。
  • 计算元素个数时，广义表中存储的每个原子算作一个数据，同样每个子表也只算作是一个数据。
    1. LS = (a1,a2,…,an) 的长度为 n；
    2. 广义表 (a,(b,c,d)) 的长度为 2；
    3. 广义表 ((a,b,c)) 的长度为 1；
    4. 空表 () 的长度为 0。
    5. 表 (()) 的长度为1，表头与表尾均为 ()。
  • 求广义表长度时，如下示意图所示：

// 计算广义表的长度
int GListLength(GList L) {
	if (L == NULL)         // 空表深度=1
		return 1;
	if (L->tag == ATOM) // 原子深度=0
		return 0;

	int length = 0;
	GList p = L ->ptr.hp;

	while (p != NULL) {
		length += GListLength(p);
        p = p->ptr.tp;
    }
	return length;
}

三、求表头

  • 非空广义表的第一个元素，可以是一个原子也可以是一个子表。
// 获取广义表的表头
GList GetHead(GList L) {
    if (L != NULL && L->tag == LIST) {
        return L->ptr.hp;
    }
    else {
        return NULL;
    }
}

四、求表尾

  • 非空广义表除去表头元素以外其它元素所构成的表，表尾一定也是一个表！
// 获取广义表的表尾
GList GetTail(GList L) {
    if (L != NULL && L->tag == LIST) {
        return L ->ptr.tp;
    }
    else {
        return NULL;
    }
}

No.4广义表的性质

  • 广义表中的数据元素有相对次序：一个直接前驱和一个直接后继。
  • 广义表的长度定义为最外层所包含元素的个数。
  • 广义表的深度定义为该广义表展开后所含括号的重数。（注意：原子深度为0，子表深度为1）
  • 广义表可以为其它广义表共享！
  • 广义表是多层次结构，其里面的元素可以是单元素，也可以是子表，而子表的元素还可以是子表。
posted @ 2023-08-05 14:22  Ghost3  阅读(41)  评论(0)  编辑  收藏  举报