2015 Dhaka
2015 Dhaka
A - Automatic Cheater Detection
solution
模拟计数。
B - Counting Weekend Days
solution
模拟计数。
C - Toll Management IV
题目描述:有一个\(n\)个点\(m\)条边的图,每条边有权值,现在给出图中一棵合法的最小生成树,问每条边权值最多增加多少,最多减少多少,使得给出的最小生成树还是最小生成树。
solution
对于给定的最小生成树,最多减少多少无界,对于其它的边,最多增加多少无界。
对于每一条非最小生成树上的边,最多减少的值为该边的两个端点在树上的路径的最大权值,而树上的路径权值最多增加到该边的边权。
因此可以用倍增的方法求出树的两点间的最大值,以及维护两点间的最多增加到的值。
时间复杂度:\(O(nlogn)\)
D - Owllen
solution
答案为出现次数最少的字母的出现次数。
E - Sum of MSLCM
题目描述:求\(1\)~\(n\)的约数的和的和。
solution
这显然是个积性函数,所以可用线性筛预处理。
时间复杂度:\(O(n)\)
F - Unique Party
题目描述:给定一个网格图,每个格子有一个值。现在有\(Q\)个询问,每次询问一个中位数(取大的那个)大于等于\(h\)的最大矩形面积。
solution
对于一个询问\(h\),将网格中大于等于\(h\)的值变为\(1\),将小于\(h\)的值变为\(-1\),则原问题相当于是求子矩阵的和非负的最大子矩阵的面积。枚举子矩阵的第一行与最后一行,求出每一列在这段区间的和,二维问题变为一维问题,求前缀和\(sum\),将区间的和变为两点的差,存在包含的区间只考虑长的那个即可,因此如果\(sum[i+1]>=sum[i]\),则\(i\)不会成为右端点。枚举右端点,左端点单调。
时间复杂度:\(O(n^3)\)
G - Honey King
题目描述:在二维蜂巢中定义坐标,给定一些坐标,求包含这些坐标的最小正六边形里面的点数。
solution
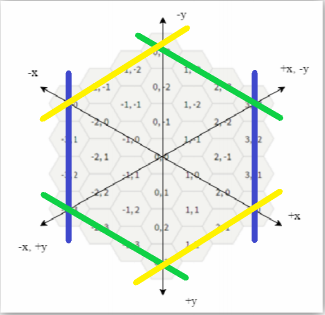
二分正六边形的边长(也可以说是正六边形的层数),如上图所示,如果以\((0, 0)\)作为中心点,那么蓝色是\(x\)坐标的界,绿色是\(y\)坐标的界,黄色是\(x+y\)的界,因此可以对每个坐标可以算出中心点的可行区间,然后判断每个坐标的可行区间的交是否有解即可。
时间复杂度:\(O(nlogn)\)
H - Design New Capital
题目描述:给定二维平面上的若干个坐标(不在坐标轴上),选择若干个坐标,使得原点是与所有选择的点的曼哈顿距离的和最小的解之一,问选择\(i\)个点的方案数。
solution
原题等价于选择的点的\(x\)坐标的中间两个数之间有\(0\),\(y\)坐标也是。所以第一象限的点数要等于第三象限的点数,第二象限的点数要等于第四象限的点数,用组合数可以算出第一,第二象限选\(i\)个数的方案,然后用\(NTT\)求卷积即可。
时间复杂度:\(O(nlogn)\)
I - Numbered Cards
题目描述:有\(n\)个数\(1\)~\(n\),问从中选择若干个数,使得任意两个数没有相同的数字的方案数。
solution
状压\(dp\)(集合\(dp\))+数位\(dp\)
状压\(dp\)记住当前用了哪些数字,枚举新的一个数用了哪些数字,然后这个新的数有多少个可以用数位\(dp\)来求。
时间复杂度:\(O(2^{10}*?*9*10)\)



