Minimum Palindromic Factorization(最少回文串分割)
Minimum Palindromic Factorization(最少回文串分割)
以下内容大部分(可以说除了关于回文树的部分)来自论文A Subquadratic Algorithm for Minimum Palindromic Factorization。
问题描述
给出一个字符串\(S\),将\(S\)划分为\(k\)个连续的字符串,使得每一个都是回文串,问\(k\)的最小值。
简单做法
直接做法就是\(O(n^2)\)的\(dp\),设\(PL[i]\)表示\(S[1..i]\)划分的最小值,集合\(P_i\)表示以\(i\)为结尾的回文串的开头位置。那么
而\(P_j\)可以由\(P_{j-1}\)推导出。总的时间复杂度为\(O(n^2)\).
更快的方法
如果\(P_j\)可以用另一个集合\(G_j\)代替,而\(G_j\)的大小只有\(O(logj)\),而且在\(O(logj)\)时间内就可以从\(G_{j-1}\)推导至\(G_j\),那么就有一个\(O(nlogn)\)的方法了。
定义1:对于一个字符串\(x\),如果\(y\)既是\(x\)的前缀,也是\(x\)的后缀,则\(y\)称为\(x\)的一个边界,如果\(y \neq x\),则\(y\)是一个真边界。
引理1:假设\(y\)是回文串\(x\)的一个后缀,则\(y\)是\(x\)的一个边界当且仅当\(y\)是一个回文串。
证明:
显然。
引理2:假设\(y\)是\(x\)的一个边界,且\(|x| \leq 2|y|\),则\(x\)是一个回文串当且仅当\(y\)是回文串。
证明:
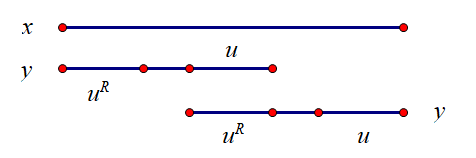
(Figure 1)
(其中\(u^R\)表示\(u\)的翻转)
定义2:假设一个字符串\(x\),如果存在一个长度为\(p(p \leq |x|)\)的字符串\(\omega\),满足\(x\)是\(\omega^{\infty}\)(无穷个\(\omega\)连接在一起)的一个字串,则\(p\)称为\(x\)的一个阶段。
显然,\(y\)是\(x\)的一个真边界当且仅当\(|x|-|y|\)是\(x\)的一个阶段,一并考虑引理1,能得出引理3。
引理3:设\(y\)是回文串\(x\)的一个真后缀,则\(|x|-|y|\)是\(x\)的一个阶段当且仅当\(y\)是回文串。特别地,\(|x|-|y|\)是\(x\)最小的阶段当且仅当\(y\)是\(x\)的最长的回文真后缀。
引理4:假设\(x\)是一个回文串,\(y\)是\(x\)的最长回文真后缀,\(z\)是\(y\)的最长回文真后缀,令\(x=uy, y=vz\),则
- \(|u| \geq |v|\)
- 若\(|u| > |v|\),则\(|u| > |z|\)
- 若\(|u| = |v|\),则\(u = v\)
证明
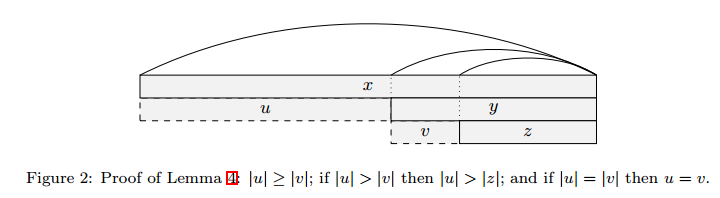
- 由引理\(3\)得,\(|u|=|x|-|y|\)是\(x\)的最小阶段,\(|v|=|y|-|z|\)是\(y\)的最小阶段。因为\(y\)是\(x\)的子串,所以\(|u| > |y| > |v|\)或\(|u|\)也是\(y\)的一个阶段。前一个结论容易理解。当\(|u| \leq |y|\)时,由Figure 1可知重叠部分为回文串,且为\(y\)的真后缀,由引理\(3\)可知\(|u|\)是一个阶段。
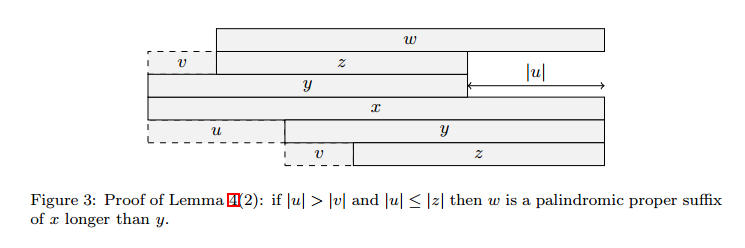
- 由引理\(1\)得,\(y\)是\(x\)的边界,\(v\)是\(x\)的前缀,设\(x=v\omega\),则\(z\)是\(\omega\)的边界且\(|\omega|=|zu|(\because x=uvz=vzu)\),因假设\(|u|>|v|\),所以\(|\omega|>|y|\)。反证法:假设\(|u| \leq |z|\),则\(|\omega|=|zu| \leq 2|z|\),有引理\(2\)得\(\omega\)是回文串,与\(y\)为\(x\)的最长回文真后缀矛盾,得证。
- 由2可知\(v\)是\(x\)的前缀,所以若\(|u|=|v|\),则\(u=v\)。
利用上述引理可以得出关于\(P_j\)的一些特性,假设\(P_j=\begin{Bmatrix} p_1, p_2, ..., p_m \end{Bmatrix}, p_1<p_2<\cdots<p_m\)。\(p_i-p_{i-1}\)称为间隔。
引理5:\(P_j\)的间隔序列是不递增的,而且最多有\(O(logj)\)个不同的间隔。
证明
\(\forall i \in [2..m-1]\)(\(m\)为\(P_j\)的大小),设\(x=S[p_{i-1}..j], y=S[p_i..j], z=S[p_{i+1}..j]\),根据引理4,有间隔\(|u|,|v|\)。根据引理4的结论1,间隔序列是不递增的。若\(|u|>|v|\),由引理4结论2得\(|x|>|u|+|z|>2|z|\),即回文后缀的长度会在两步内变成一半,所以最多有\(O(logj)\)个不同的间隔。
将\(P_j\)按间隔分成\(O(logj)\)个连续的子集,每个集合的间隔相等,即设\(P_{j, \Delta}=\begin{Bmatrix} p_i: 1 < i <m, p_i-p_{i-1}=\Delta \end{Bmatrix}, P_{j, \infty}=\begin{Bmatrix} p_1 \end{Bmatrix}\)。每一个\(P_{j, \Delta}\)用一个三元组表示\((min P_{j, \Delta}, \Delta, |P_{j, \Delta}|)\)。设\(G_j\)为一个链表,以\(\Delta\)递减的顺序存在这些三元组。
\(G_j\)的大小最大为\(O(logj)\),接下来会讲如何在\(O(|G_{j-1}|)\)时间内将\(G_{j-1}\)转移至\(G_j\)。在平方的算法中,需要对\(P_{j-1}\)的每个元素判断是去掉还是替换为减一。以下的引理可证明这一决策对\(P_{j-1, \Delta}\)能同时操作。
引理6:设\(p_i\)和\(p_{i+1}\)是\(P_{j-1, \Delta}\)的两个连续的元素,则\(p_i-1 \in P_j\)当且仅当\(p_{i+1}-1 \in P_j\)
证明
根据定义,\(p_{i+1}-p_i=\Delta\),而且\(p_{i-1}=p_i-\Delta\)。根据引理4结论3,\(S[p_i-1]=S[p_{i+1}-1]=c\),所以\(p_i-1 \in P_j\)当且仅当\(S[j]=c\),即当且仅当\(p_{i+1}-1 \in P_j\)。
所以每个三元组\((i, \Delta, k) \in G_{j-1}\)或是去掉或是用\((i-1, \Delta, k)\)。即
但是\(G'_j\)可能不满足定义,因为某些间隔改变了。准确的说,当\(P_{j-1, \Delta}\)的最小元素\(p_i\)替换成了\(p_i-1\),但\(p_{i-1}=p_i-\Delta\)被去掉了(因为\(p_{i-1}\)不符合引理4结论3,有可能\(S[p_{i-1}-1] \neq S[j]\)),则\(p_i-1\)不再属于\(P_{j, \Delta}\)。这时需要把\(p_i-1\)单独拆分,即将\((p_i-1, \Delta, k)\)分成\((p_i-1, \Delta', 1)\)和\((p_i-1+\Delta, \Delta, k-1)\)(如果\(k>1\)),其中\(\Delta'\)为新的间隔。在这过程中还需要合并相同间隔的三元组。(详细可看最后的代码)
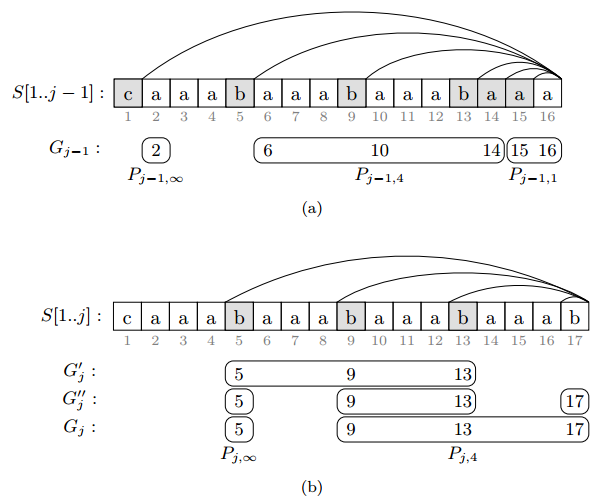
引理7:\(G_j\)能在\(O(|G_{j-1}|)=O(logj)\)时间内从\(G_{j-1}\)推导出。
接下来说明如何在\(O(|G_j|)\)的时间内,利用\(PL[j-1], G_j\)推导出\(PL[j]\)。
引理8:若\((i, \Delta, k) \in G_j, k \geq 2)\),则\((i, \Delta, k-1) \in G_{j-\Delta}\)
证明
根据定义,\((i, \Delta, k) \in G_j\)等价于\(P_{j, \Delta}=\begin{Bmatrix} i, i+\Delta, ..., i+(k-1)\Delta \end{Bmatrix}\),现需要证明\(P_{j-\Delta, \Delta}=\begin{Bmatrix} i, i+\Delta, ..., i+(k-2)\Delta \end{Bmatrix}\)。现在先证明\(P_{j-\Delta, \Delta} \cap [i-\Delta+1..j-\Delta]=\begin{Bmatrix} i, i+\Delta, ..., i+(k-2)\Delta \end{Bmatrix}\),而且\(P_{j-\Delta, \Delta} \cap [1..i-\Delta]=\varnothing\)
因为\(y=S[i..j], x=S[i-\Delta..j]\)(根据\(\Delta\)的定义)都是回文串,而且\(y\)是\(x\)最长的真边界,\(S[i-\Delta..j-\Delta]=y=S[i..j]\)。所以对于\(\forall l \in [i..j], l \in P_j\)当且仅当\(l-\Delta \in P_{j-\Delta}\)。特别地,因为间隔相同,所以\(\forall l \in [i+1..j], l \in P_{j, \Delta}\)当且仅当\(l-\Delta \in P_{j-\Delta, \Delta}\)。所以\(P_{j-\Delta, \Delta} \cap [i-\Delta+1..j-\Delta]=\begin{Bmatrix} i, i+\Delta, ..., i+(k-2)\Delta \end{Bmatrix}\)。
现在还需证明\(P_{j-\Delta, \Delta} \cap [1..i-\Delta]=\varnothing\)。这为真当且仅当\(i-2\Delta \notin P_{j-\Delta}\)。反证法:\(S[i-2\Delta..j-\Delta]\)是回文串,设\(\omega=S[i-2\Delta..i-\Delta-1]\),则\(S[j-2\Delta+1..j-\Delta]=\omega^R\)。因为\(z=S[i-\Delta..j-\Delta]\)和\(S[i-\Delta..j]\)都是回文串,所以\(S[i-\Delta..i-1]=\omega, S[j-\Delta+1..j]=\omega^R\)。因为\(z\)是回文串,所以\(S[i-2\Delta..j]=\omega z \omega^R\)也是回文串,所以\(i-2\Delta \in P_j, i-\Delta \in P_{j, \Delta}\),矛盾,得证。而且\(i-2\Delta \notin P_{j-\Delta}\)一定成立,若\(i-2\Delta in P_{j-\Delta}\),则\(P_{j-Delta, \Delta}\)的最小元素不是\(i\)。
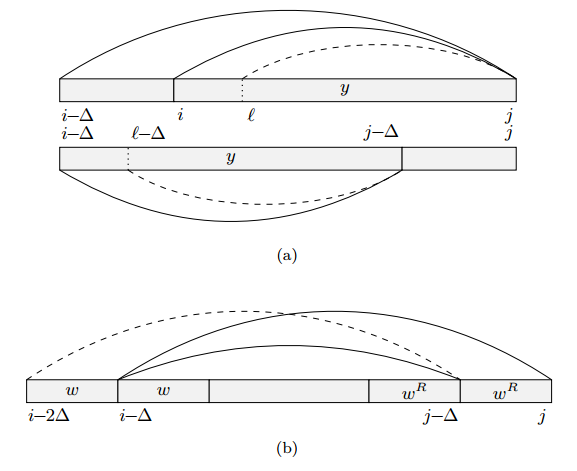
所以\(P_{j, \Delta}=P_{j-\Delta, \Delta} \cup max P_{j, \Delta}\)(当\(|P_{j, \Delta} \geq 2\))。这样\(PL_{j, \Delta}=min{PL[i-1]+1 : i \in P_{j, \Delta}}\)就能利用\(PL_{j-\Delta, \Delta}\)在常数时间内得出。
设\(GPL[i]\),\(GPL[m=min(P_{j, \Delta}-\Delta]=PL_{j, \Delta}\),注意到\(PL_{j-\Delta, \Delta}\)也是存在\(m\)这个位置(若\(|P_{j, \Delta} \geq 2\))。以下引理证明位置\(m\)在\((j-\Delta..j)\)不会被其它数重写。
引理9:设\(m=min(P_{j, \Delta}-\Delta), \forall l \in [j-\Delta+1..j-1], m \notin P_l\)
证明
反证法:假设\(m \in P_l, l \in [j-\Delta+1..j-1]\),则\(S[m..l]\)是回文串,则\(S[m+h..l-h], h=l-j+\Delta\)也是回文串。因为\(l-h=j-\Delta, m<m+h<m+\Delta=min(P_{j-\Delta, \Delta})\),所以\(m+h\)才是\(min(P_{j-\Delta, \Delta})\)在\(P_{j-\Delta}\)中的前一个,\(min(P_{j-\Delta, \Delta}) \notin P_{j-\Delta, \Delta}\),矛盾,得证。
定理:将一个长度为\(n\)的字符串分解成最少回文串可以在时间复杂度为\(O(nlogn)\),空间复杂度为\(O(n)\)下算出。
/*
tripe{nid, delta, sum}(开头位置, 间隔, 个数)
*/
memset(PL, 0x7f, sizeof PL);
memset(GPL, 0x7f, sizeof GPL);
PL[0]=0;
vtri G;
G.clear();
for (int j=1; j<=n; ++j)
{
vtri h;
h.clear();
int r=-j; //前者结尾位置
for (auto &i : G)
if (i.nid>1 && st[i.nid-1]==st[j])
{
int nid=i.nid-1;
if (nid-r!=i.delta) //间隔不同
{
//拆分
h.push_back(tripe{nid, nid-r, 1});
if (i.sum>1)
h.push_back(tripe{nid+i.delta, i.delta, i.sum-1});
}
else h.push_back(tripe{nid, i.delta, i.sum}); //间隔相同
r=nid+(i.sum-1)*i.delta; //更新前者结尾位置
}
if (j>1 && st[j-1]==st[j]) //长度为2的回文串
{
h.push_back(tripe{j-1, j-1-r, 1});
r=j-1;
}
h.push_back(tripe{j, j-r, 1}); //长度为2的回文串
G.clear();
//合并相同间隔的三元组
G.push_back(*h.begin());
for (vtri::iterator it=h.begin()+1; it!=h.end(); ++it)
if (G.back().delta==(*it).delta) G.back().sum+=(*it).sum;
else G.push_back(*it);
PL[j]=j;
for (auto &i:G)
{
int r=i.nid+(i.sum-1)*i.delta;
int m=PL[r-1]+1;
if (i.sum>1) m=min(m, GPL[i.nid-i.delta]);
if (i.delta<=i.nid) GPL[i.nid-i.delta]=m;
PL[j]=m;
}
}
}
与回文树的结合
回文树可以维护以某个点为结尾的回文串,而且回文树中的\(fail[i]\)指向的是长度仅次于\(i\)的回文串的回文串。也就是说沿着\(fail\)走到\(root\)得到的路径就是以\(i\)为结尾的回文串,而且设\(diff\)为路径中相邻两个点的\(len\)的差,则\(diff\)就是间隔序列,而且这个间隔序列是满足上述的性质的,所以可以另外设一个数组\(anc\)来维护\(i.nid\)(同一个\(\Delta\)的开头位置)的位置,时间复杂度也是\(O(nlogn)\)。
void init() //回文树初始化
{
S[0]=-1;
m=0; //字符串长度
total=1; //回文树点数
last=0; //最后插入的点
len[0]=0; //回文串长度
len[1]=-1;
fail[0]=fail[1]=1;
}
void insert(int ch)
{
S[++m]=ch;
int cur=last;
while (S[m-len[cur]-1]!=S[m]) cur=fail[cur];
if (!son[cur][ch])
{
len[++total]=len[cur]+2;
int tmp=fail[cur];
while (S[m-len[tmp]-1]!=S[m]) tmp=fail[tmp];
tmp=son[tmp][ch];
fail[total]=tmp; son[cur][ch]=total;
diff[total]=len[total]-len[tmp]; //间隔序列
anc[total]=(diff[total]==diff[tmp]? anc[tmp]:tmp); //开头位置
}
last=son[cur][ch];
}
void solve()
{
init();
for (int i=1; i<=n; ++i) ans[i]=inf;
for (int i=1; i<=n; ++i)
{
insert(a[i]);
for (int j=last; j; j=anc[j])
{
hd[j]=i-len[anc[j]]-diff[j]; //GPL存放位置
if (anc[j]!=fail[j] && ans[hd[fail[j]]]<ans[hd[j]])
hd[j]=hd[fail[j]];
if (!(i & 1) && ans[hd[j]]+1<ans[i]) ans[i]=ans[hd[j]]+1;
}
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号