2017 ACM ICPC Asia Regional - Daejeon
2017 ACM ICPC Asia Regional - Daejeon
Problem A Broadcast Stations
题目描述:给出一棵树,每一个点有一个辐射距离\(p_i\)(待确定),但\(p_i==0\)的点不能辐射自己,只能由别的点辐射覆盖。求\(p_i\)的和的最小值。
Problem B Connect3
题目描述:有一个\(4 \times 4\)的网格,两个人玩游戏,第一个人用黑棋,第二人用白棋。每次选择一列,将棋子扔下去,直到最下一个空的格子。现在给出第一个人下的位置,以及最后第二个人下的棋子最终的位置。已知最后一步是赢棋的一步,问最终有多少种棋盘状态。
solution
因为状态数很少,所以可以直接暴力搜索最终的状态。
时间复杂度:\(O(2^{16}*16)\)
Problem C Game Map
题目描述:给出一个\(n\)个点的图,设每个点的度为\(d_i\),选出一个最长的序列\(c_i\),满足\(d_{c_i}<d_{c_{i+1}}\),且\(c_i\)与\(c_{i+1}\)相邻,输出最长的长度。
solution
将点按度排序,每个点\(i\)向度比\(d_i\)大的邻居连一条有向边,然后DAG \(dp\)。
时间复杂度:\(O(n)\)
Problem D Happy Number
题目描述:设函数\(f(n)\),\(f(n)\)等于\(n\)的每一位的数的平方的和,将得出的结果继续带进\(f\)继续算,直到等于\(1\),如果能等于\(1\),则称\(n\)是开心的数,否则是不开心的数。给出一个数\(n\),判断是否是开心的数。
solution
暴力模拟,记忆化\(n \leq 1000\)的数是否开心。
时间复杂度:\(O(1000*10)\)
Problem E How Many to Be Happy?
题目描述:给出一个有\(n\)个点\(m\)条边的图,每条边有一个边权,问要使第\(i\)条边成为图的最小生成树的一条边最少要删掉多少条边,求出每条边的对应答案的和。
solution
枚举边\(i\),找出那些边权小于\(i\)的边权的边,这些边都是网络流里的边,然后以\(i\)的两个点为源点和汇点跑网络流求最小割。
时间复杂度:\(O(mn^2m)\)(远小于这个值)
Problem F Philosopher’s Walk
题目描述:按以下规则构建路线:其中\(W_i\)的左上角和右上角都是\(W_{i-1}\),左下角为\(W_{i-1}\)顺时针转\(90^{\circ}\),右下角为\(W_{i-1}\)逆时针转\(90^{\circ}\)。从\((1, 1)\)出发沿线编号。给出\(x, y\),求出\(W_x\)中编号为\(y\)的格子坐标。
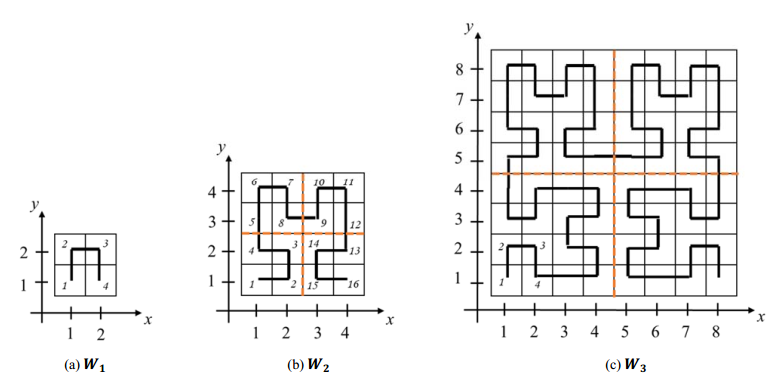
solution
分治求解,缩减图的规模,递归回来之后进行坐标变换即可。
时间复杂度:\(O(k)\)
Problem G Rectilinear Regions
题目描述:给出两条阶梯型的线\(L, U\),求出那些\(U\)在上,\(L\)在下围成的多边形的面积的和。
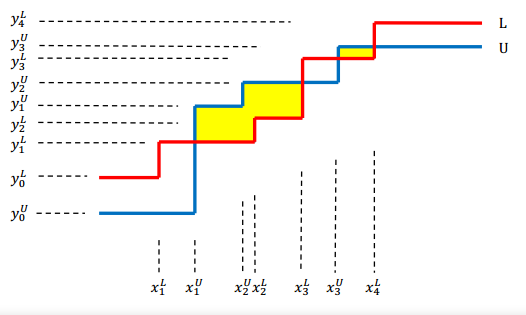
solution
观察可得,多边形的左边为\(U\)的竖线与\(L\)的横线相交,右边为\(U\)的横线与\(L\)的竖线相交。枚举\(U\)的每一级,二分出\(L\)对应的位置,判断是否相交。将相交的地方映射到\(x\)轴,若相邻的相交类型是上述的类型,就用部分和算出围成的多边形的面积。
时间复杂度:\(O(nlogn)\)
Problem H Rock Paper Scissors
题目描述:给出两个剪刀(S)石头(R)布(P)的序列,确定第一个序列的一个位置作为第二个序列的开始位置,算出第二个序列能多少局。求出第二个序列最多能赢多少局。
solution
先将第一个序列的每一位变成能赢这一位的字符。问题变成一个匹配问题。
将这个序列分成三个序列,每个序列分别只有剪刀、石头、布。同样将第二个序列分成三个序列,每个序列分别只有剪刀、石头、布。
例如:
RSPPSSSRRPPR 先变成 PRSSRRRPPSSP
RRRR
将石头序列拿出来,假设第一个序列为\(a_i\),第二个序列为\(b_i\)。按照上述的例子:
\(a=010011100000\)
\(b=1111\)
设\(f_i\)表示以\(i\)开头的区间的匹配数目,则\(f_i=\sum_{j=0}^{j<|b|} a_{i+j}*b_j\),若将\(a_i\)翻转,则\(f_{n-i}=\sum_{j=0}^{j<|b|} a_{n-(i+j)}*b_j\),就是卷积。
同理算出剪刀序列和布序列,求和,求最大值。
时间复杂度:\(O(9nlogn)\)
Problem I Slot Machines
题目描述:给出一个长度为\(n\)的序列\(a_i\),这个序列第\(k+1\)起到最后是若干个循环,周期为\(p\),最后一个循环可以不完整。求\(k+p\)最小值对应的\(k, p\)。
solution
将序列\(a_i\)翻转,做一次\(KMP\)(\(fail[i]\)),枚举\(k+1\)的位置\(i\),则周期\(p=i-fail[i], k=n-i\)。更新答案。
时间复杂度:\(O(n)\)
Problem K Untangling Chain
题目描述:在二维平面上,从\((0, 0)\)出发(开始时向右走),向前走一段距离(整数),然后向左转或向右转,重复若干次。给出路径,改变每一次走的距离(不能改变转向),使得路径不相交。输出一种方案。
solution
记录\(x, y\)的最大最小值,每次走的时候走到对应的边界加一即可。
时间复杂度:\(O(n)\)
Problem L Vacation Plans
题目描述:给出\(s(s \leq 3)\)个图,每个图是一个有向图(\(n\)点,\(m\)条边),有点权,有边权。每个图有一个目的地,出发点都是\(1\),每一时刻经过一条边,花费为边权,或者停止不动,花费为点权。现要求同时出发,同时到达目的地,问总花费的最小值。
solution
枚举时间,三个图同时\(dp\),更新答案,卡一下时就可以了,兜圈不会兜很多遍。
时间复杂度:\(O(n^sms)\)



