Petrozavodsk Summer Training Camp 2017 Day 9
Petrozavodsk Summer Training Camp 2017 Day 9
Problem A. Building
题目描述:给出一棵树,在树上取出一条简单路径,使得该路径的最长上升子序列最长,问最长的长度。
solution
最常见的想法就是树状dp,但空间不太够,所以选择直接计数。
每个点记住两个\(vector(f, g)\),\(f_i\)表示从叶子到\(i\)的最长的递增序列,\(g_i\)表示从叶子到\(i\)的最长的递减序列。
当算以\(i\)为根的子树的答案时,假设做到儿子\(j\),算\(f[i]\)与\(g[j]\)组成的最长递增序列,以及\(f[j]\)与\(g[i]\)的最长递增序列。算的时候一个序列枚举每个数,然后在另一个序列二分出位置,即可更新答案,而枚举的序列要选短的那个,这样时间复杂度就能保证为\(log^2n\),还要注意答案序列经过\(i\)的情况。
然后就是将\(f[i]、f[j]\),\(g[i]、g[j]\)合并。拿\(f[i]、f[j]\)合并为例子,合并的时候直接取对应位置的最小值即可,即:
2 3 4 6 7
1 2 5 8
合并为1 2 4 6 7.
对于\(f\)序列,数越小越好,因为对于相同的位置\(k\),它在答案序列的位置就是\(k\),这是固定的,而数越小,就可以在\(g\)找到更多的数来拼成序列,得到更大的答案。
同样的道理,对于\(g\)中的数找\(f\)对应的位置,对于相同的数,\(f\)的数越小,二分出的位置不会更差,反而有可能更优。
因此对于\(g\)序列,数越大越好。
时间复杂度:\(O(nlog^2n)\)
Problem B. Fish
题目描述:有\(n\)条鱼,每条鱼的长度为\(L_i\),颜色是\(c_i\),颜色只有三种('R', 'G', 'B')。现要取出一个非空子集,使得任意一条鱼的长度小于任意一条鱼的长度的两倍,假设选出的子集的每种颜色数目为三元对\((x, y, z)\),问三元对的数目。
solution
将鱼按长度从小到大排序,对于每条鱼\(i\),找到最大的\(j\),满足\(L_j<L_i*2\),部分和求出\([i, j]\)的每种颜色的数目\((x_i, y_i, z_i)\)。问题转化为有\(n\)个三元对\((x_i, y_i, z_i)\),求三元对\((x, y, z)\)的数目,满足存在一个\(i\),\(x \leq x_i, y \leq y_i, z \leq z_i\)。
这就跟codeforces上的一道题很像(Karen and Cards),至少思路很像。
这里我们将三元对从大到小排序,记每个\(y\)对应的最大的\(z\)为\(maxz[y]\)。对于每一个\(x\),用\(x_i==x\)的三元对更新\(maxz[y]\),这里要利用\(maxz[y]\)的一个特点:\(maxz[y]\)是递减。所以可以二分出要更新的区间,然后用线段树维护\(maxz[y]\)。然后对于\(x\),答案就是\(\sum maxz[y]\)。
时间复杂度:\(O(nlogn)\)
Problem C. JOI Flag
题目描述:定义\(level-K\)的\(JOI Flag\):
- 一个\(level-0\)的\(JOI Flag\)是一个\(1 \times 1\)的网格图,包含'J', 'O', 'I'其中一个字母。
- 当\(m>0\)时,一个\(level-m\)的\(JOI Flag\)是一个\(2^m \times 2^m\)的网格图,能分成四个\(2^{m-1} \times 2^{m-1}\)的网格图:一个是\(level-m-1\)的\(JOI Flag\),一个全是'J', 一个全是'O',一个全是'I'。
现在有一个\(2^K \times 2^K\)的网格图,里面有些格子的字母是确定的,未知的位置可以随便填字母而不需要花费,改变已知的字母则需要花费\(1\)。问将这个网格图变成一个\(level-K\)的\(JOI Flag\)需要的最小花费。
solution
因为已知的字母比较少,所以可以直接暴力搜索。
时间复杂度:\(O(4!NK)\)
Problem E. Rotate
题目描述:给出一个\(N \times N\)的网格图,每个格子有一个小写字母。现在有\(Q\)次操作,每次操作选择一个子方阵,将子方阵逆时针旋转\(90^{\circ}\)。输出最后的网格图。
solution
一开始的想法是将每一行,每一列压位,然后暴力旋转,时间复杂度是\(O(QN^2/13)\)。但写起来非常恶心。
在网格图外围再围一层,变成\((N+2) \times (N+2)\)的网格图,然后从\(0\)到\(n*n-1\)编号\((n=N+2)\),记录每个编号\(i\),左上右下的编号。
当进行一次旋转操作时,只有子方阵的边界的左上右下的编号会改变,子方阵内部的也会改变,但改变的只是编号对应的方向,也就是说还是那四个编号,只是方向发生了改变,而且这个改变是轮换,即方向的相对位置没有发生变化。例如:
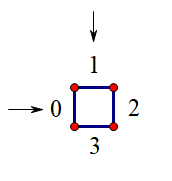
只要是沿当前方向向前走,不管是从\(0\)进来还是\(1\)进来,都是从\(+2\)的位置出去,只要是右拐,都是从\(-1\)的位置出去。所以每次只需要修改子方阵边界的各个方向的编号,内部的不需要修改。
定位子方阵的左上角时,从\(0\)开始向右走(最外围不会被改变),走到对应列右拐,向前走走到对应行,然后围着子矩阵边界转一圈。注意这里行走时用的描述都是向前,拐弯,不是上下左右,因为只能保证相对位置不变,去哪一个编号也跟从哪里来有关。输出答案时从每一行的边界开始向右(最左边一列不变)前进即可。
时间复杂度:\(O(QN)\)
Problem F. Fortune Telling
题目描述:有一个\(M \times N\)的网格图,每个格子开始时都是白色,现在有\(K\)个操作,每次操作将一个子矩阵的颜色翻转,即黑变白,白变黑。问最终有多少个格子是白色。
solution
离散化+扫描线+线段树。
时间复杂度:\(O(nlogn)\)
Problem G. Kangaroo
题目描述:有\(n\)只袋鼠,每只袋鼠的大小为\(A_i\),袋子的大小为\(B_i\)。每只袋鼠只能装一只袋鼠,但允许那只袋鼠的袋子里也有袋鼠,当\(A_j<B_i\)时,袋鼠\(j\)就能装到\(i\)的袋子里。问最后的状态有多少种(能装就要装)。
solution
转队友的题解
Problem I. Chinese
题目描述:在圆桌上等分地放着\(n\)盘菜,顺时针或逆时针旋转一个单位需要一个花费。现在给出\(2\)~\(n\)每个人要吃的菜,开始时第\(i\)个人对着第\(i\)盘菜,第一个人最先吃(对着就能吃),吃完后其他人再吃,其他人吃时不分顺序,输出当第一个人吃第\(i\)盘菜时,所有人吃完菜的最少花费。
solution
算出从初始开始顺时针转,使得第\(i\)个人吃上菜的花费\(a_i\),因为是环,惯用技巧是将\(a\)数组复制一遍在后面。
枚举\(i\)(\(1\)~\(2*n-1\))表示第一个人吃第\(i\)盘菜,求出\(j\)使得\(\sum_{k=i}^{j} a_k==n-1\),则\(j-i\)是一种方案,假设\(x\)为\(i-1\)时的最优方案,则\(x+1\)也是一种方案,即花费\(1\)转回去,然后用\(i-1\)时的最优方案。
反过来枚举\(i\)(\(2*n\)~\(1\)),然后按上述的做法重做一次,表示逆时针转。
这两种方法已经涵盖了所有的最优方案。当第一个人吃第\(i\)盘菜时,方案有四个:1、顺时针转,2、逆时针转,3、先顺时针转再逆时针转,4、先逆时针转再顺时针转。而上述方法中的花费\(1\)转回去,就是方案3、4。
时间复杂度:\(O(n)\)



