2017-2018 ACM-ICPC, NEERC, Northern Subregional Contest
2017-2018 ACM-ICPC, NEERC, Northern Subregional Contest
Problem A. Auxiliary Project
题目描述:用摆成一个\(8\)字的七盏LED灯来显示数字\(0\)~\(9\),现要允许亮\(n\)盏灯,问形成的数字的和最大是多少。
solution
完全背包。
时间复杂度:\(O(10n)\)
Problem B. Boolean Satisfiability
题目描述:给出一个只有\(OR, NOT\)运算符的式子,每个变量都是布尔变量,问有多少种赋值方案使得式子最终是\(true\).
solution
求补集,因为运算符只有\(OR, NOT\),所以如果一个变量既有本身又有\(NOT\),则式子一定是\(true\),否则只存在一种方案使得式子为\(false\)。
时间复杂度:\(O(字符串长度)\)
Problem C. Consonant Fencity
题目描述:定义一个字符串的值:若相邻的字符都是辅音字母(不算'y, w'),而且大小写不一样,则字符串的值加一。给出一个由小写字符组成的字符串,确定哪些种类的字符变成大写,使得最后字符串的值最大,输出对应的字符串。
solution
搜索每种字母是大写还是小写。然后算出字符串的值,因为相邻字符都是辅音字母只有\(19^2\)种情况,所以可以预处理出每种情况在字符串出现多少,这样就可以在\(19^2\)内算出字符串的值。
时间复杂度:\(O(2^{19} \times 19^2)\)
Problem D. Dividing Marbles
题目描述:给出四个数字\(d_1, d_2, d_3, d_4\),有一堆个数为\(2^{d_1}+2^{d_2}+2^{d_3}+2^{d_4}\)的石子,进行以下操作:1、选择一堆大于\(2\)的石堆,将其分成两堆,每堆个数至少为\(1\)。2、如果有若干堆石子的个数相同,则只留下一堆。
最后只剩下一堆一个石子。问最少需要多少步\(1\)操作,并输出每一步\(1\)操作。
solution
还不会。。。
Problem E. Equal Numbers
题目描述:给出一个序列\(a_i\),每次选其中一个数乘以一个正整数,问进行\(k\)步操作后最少剩下多少种数字,输出\(0 \leq k \leq n\),所有的\(k\)的答案。注意这\(k\)步不一定是连续的。
solution
有两种较优的操作方案:
- 先将有倍数的数变成它们的最大倍数,而且按照出现次数比较少的先变
- 将所有数都变成\(lcm\),而且按照出现次数比较少的先变
每一步取两种操作的最小值
时间复杂度:\(O(nlogn)\)
Problem F. Fygon 2.0
题目描述:给出一个只有for语句的程序(只有最内层的for有一句表达式),设那句表达式执行了\(f(n)\)次,令\(\lim_{n \to \infty} \frac{f(n)}{Cn^k}=1\),求\(C, k\)。
solution
听完大神讲解后还没理清思路。。。
Problem G. Grand Test
题目描述:给出一个图,在图中找出两个点,满足这两个点之间至少有三条没有点相交的路径。输出这两个点以及对应的三条路径。
solution
构建\(dfs\)树,树上除了树边就是返祖边。如果存在一个节点\(cur\),它的两个儿子的子树中各存在一个节点有一条返祖边,且返祖边连着的点是\(cur\)的祖先,则祖先较低的和\(cur\)就是那两个点。下图为三条路径:
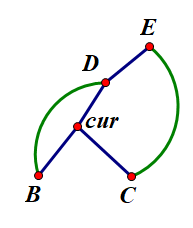
其中那两个点为\(cur, D\)为答案的两个点。第一条路径为\(cur \to D\),第二条为\(cur \to B \to D\),第三条为\(cur \to C \to E \to D\)。
时间复杂度:\(O(n)\)
Problem H. Hidden Supervisors
题目描述:有一棵树,给出这棵树一些点的父亲,重构出一棵满足条件的树,使得能选出的点对数最多,那些点对满足父亲儿子关系且每个点只能存在于一个点对中,输出这棵树。
solution
给出的条件是一个森林,先处理每棵树的匹配问题(贪心就好),然后记住那些没有匹配的点以及没有父亲又没有匹配的点,然后贪心地匹配这两类点,剩下的点直接连向\(1\)即可。
时间复杂度:\(O(n)\)
Problem I. Intelligence in Perpendicularia
题目描述:给出一个多边形,这个多边形的边平行于\(x, y\)轴。问从上下左右向多边形看,有多少长度的边看不到。
solution
多边形周长\(-\)外围矩形周长
时间复杂度:\(O(n)\)
Problem J. Joker
Problem K. Kotlin Island
题目描述:有一个全是.的\(h \times w\)网格图,将某些行、某些列变成#,使得.连通块恰好有\(n\)个。输出最后的网格图。
solution
隔一行,隔一列变#,而这样连通块的数量最多而且是一个矩形,所以可以把\(n\)分解成两个数相乘,然后尝试将矩形填进去即可。
时间复杂度:\(O(\sqrt {n})\)
Problem L. Little Difference
题目描述:给出一个整数\(n\),将其分成若干个数相乘,满足这些数的两两的差的绝对值不超过\(1\),输出所有方案,或是\(-1\)表示无限种方案。
solution
显然,当\(n=1\)或是\(2\)的幂时,有无限种方案。
否则最多有\(logn\)种方案,因为当\(n\)分解成\(m\)个数相乘时,最多只对应一种方案,而且这\(m\)个数为\(log_m n\)或\((log_m n)+1\)。所以可以特殊处理一下\(m=2\)的情况,然后设\(x=log_3 n\),\(x\)是随着\(m\)的递增而不断递减的。
时间复杂度:\(O(10^6)\)



