Codeforces Round #455 (Div. 2)
Codeforces Round #455 (Div. 2)
A. Generate Login
题目描述:给出两个字符串,分别取字符串的某个前缀,使得两个前缀连起来的字符串的字典序在所有方案中最小,输出该字符串。
solution
为保证字典序最小,第二个字符串只会选第一个字符,然后先选上第一个字符串的第一个字符(因为不能为空),接着从第二个字符开始,如果该字符小于第二个字符串的第一个字符,那么选上,否则停止,输出答案。
时间复杂度:\(O(n)\)
B. Segments
题目描述:给定一个数\(N\),考虑数轴上的所有端点均为整数且在\([0, N]\)的线段,显然有\(\frac{n(n+1)}{2}\),现将这些线段置于不同层,使得同一层的线段不重叠(端点不算),问最少要多少层?(下图为\(N=4\)时)
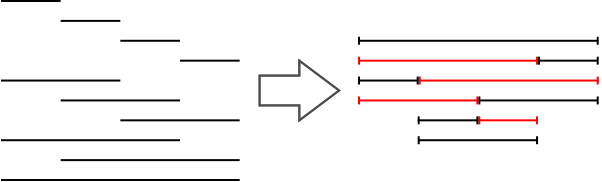
solution
考虑长度为一的线段,所有与该线段重叠的线段均在不同层,所以答案至少为\((\frac{n}{2}+1)\frac{n+1}{2}\),事实上,这个就是答案,题解中也没讲得很清楚,只是说可以构造出来
时间复杂度:\(O(n)\)
C. Python Indentation
题目描述:给出一段简略版无缩进的Python代码(只有for和简单语句),问有多少中缩进满足Python语法。
solution
设\(f[i][j]\)表示到第\(i\)条语句缩进了\(j\)次,当第\(i-1\)条语句为for时,第\(i\)条语句必须缩进,所以\(f[i][j]=f[i-1][j-1]\),若不是for则假设第\(i\)条语句缩进\(j\)次,那么这个状态可以从\(f[i-1][k], (k>=j)\)转移过来,也就是后缀和。
时间复杂度:\(O(n^2)\)
D. Colorful Points
题目描述:给定一个只有小写字母的字符串,每次操作选出字符串中与相邻位字母不一样(任意一个即可)的位置,然后删除,剩下的拼接在一起,问能执行多少次这样的操作
solution
因为如果与相邻位字母都相同的话,该字母不会被删除,所以可以把相邻的相同字母看成一组,假设有\(D\)组,每组有\(G(D)\)个字母,因此每一次操作只会把每一组的最左边和最右边删掉。每次求出最少操作数使得某个\(G(D)=0\),更新答案,并更新每组剩下的字母个数,并且进行必要的合并,这里的时间复杂度为\(D\),但每次更新后字母数至少减少\(D\)个,因此总的时间复杂度为\(O(n)\)
时间复杂度:\(O(n)\)
Coprocessor
题目描述:给定一个拓扑图表示依赖关系,并给定每个点(任务)必须在主进程执行还是副进程执行。开始时在主进程,每个任务执行前,它所依赖的任务必须已经执行,在主进程中可以调用副进程,每次调用时都可以执行若干个任务,但每个任务的依赖任务必须在该次调用中或已经执行了,副进程结束后会返回主进程。问至少需要调用多少次副进程才能完成所有任务。
solution
从叶子节点往上dp,假设当前节点为\(i\),\(f[i]\)表示完成该子树的所有任务至少需要调用多少次副进程。如果节点\(i\)必须在主进程执行,那么(\(j\)为\(i\)的儿子)
如果\(i\)必须在副进程执行,则\(f[i]=max\){\(f[j]\)}
为了方便,可以添加一个主进程任务\(0\),它的依赖为所有进程,最终答案就是\(f[0]\)
时间复杂度:\(O(n)\)
F. AND-permutations
题目描述:给定一个整数\(N\),寻找两个\(N\)排列:
- \(p_i \neq i\)且\(p_i \& i=0\)
- \(p_i \neq i\)且\(p_i \& i \neq 0\)
若不存在,则输出NO
solution
考虑第一个排列。
当\(N\)为奇数时,不存在第一个排列,因为当\(i\)为奇数时,\(p_i\)为偶数(否则二进制最低位为\(1\)),但奇数个数与偶数个数不相等,所以无解。
当\(N\)为偶数时,注意到\((2^k+i) \& (2^k-i-1)\)等于0(\(i \geq 0\)),所以可以找出最大的\(k\)使\(2^k \leq N\),然后构造解,更新\(N=2^{(k+1)}-N-2\),直至\(N=0\)
考虑第二个排列。
手工构造可知,当\(N<6\)时无解,当\(N=6\)时,解为\(3,6,2,5,1,4\),当\(N=7\)时,解为\(7,3,6,5,1,2,4\)。
当\(N>7\)时,因\(8\)~\(15\), \(16\)~\(31\), \(32\)~\(63\), ... , 每组的最高位一致,所以这些数各组循环移动一位即可。
时间复杂度:\(O(n)\)



