URAL题解一
URAL题解一
URAL 1002
题目描述:一种记住手机号的方法就是将字母与数字对应,如图。这样就可以只记住一些单词,而不用记住数字。给出一个数字串和n个单词,用最少的单词数来代替数字串,输出对应的任一方案。

solution
首先想到的应该是DP,接着就是状态转移的问题,也就是预处理出每个单词可以与哪一段的数字对应,分析时间复杂度,发现直接暴力判断是可以的,但用HASH会好一些,还可以用KMP。
时间复杂度:\(O(单词数*数字长度)或O(单词长度*数字长度)\)
URAL 1010
题目描述:有一个离散函数,它的定义域为整数\([1, n]\),现在在函数图象中找两个点,使得这两个点之间的点都在这两个点的连线的下方,求出连线倾斜度最大的方案(两个点,编号小的在前),有多个方案时输出第一个点编号最小的方案。
solution
首先考虑比较特殊的方案:相邻的两个点。相邻的两个点肯定是可行的。然后考虑两点之间有点的可行方案。
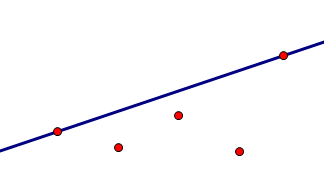
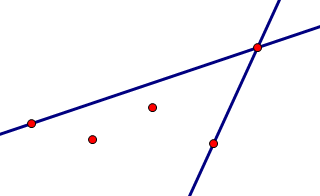
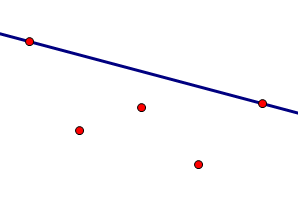
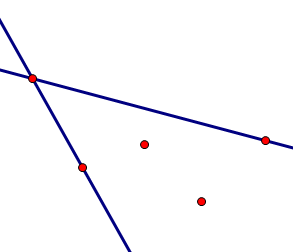
由上图可知,与选取的两点\((i, j)\)相邻的点必定有一个点与i或j相连的直线的倾角比\((i, j)\)所成的直线的倾角要大,所以中间有点的方案不是最优方案,所以答案就是相邻的点形成的直线的倾角最大的方案。
时间复杂度:\(O(n)\)
URAL 1011
题目描述:有\(n\)个人,其中有\(m\)个是乘务员,已知乘务员的比例大于\(P\)%,小于\(Q\)%,问\(n\)最小是多少。
solution
按题意列出公式
$ P$ % \(< \frac{m}{n} < Q\) %
化简
\(P\) % \(n<m< Q\) % \(n\)
题目就变成:找出最小的\(n\),使得区间\((P\) % \(n ,Q\) % \(n)\)中至少有一个整数。显然\(n<100000\),所以直接枚举即可。
时间复杂度:\(O(n)\)
URAL 1012
题目描述:在所有没有前导\(0\)的\(n\)位\(k\)进制数中,没有连续两个\(0\)的数有多少个。
solution
很明显是数位DP,但答案很大,要高精度。
时间复杂度:\(O(n^2)\)
URAL 1017
题目描述:用\(n\)个木块排成一个楼梯,楼梯每一级的高度至少要比前一级高一个木块,楼梯至少有两级,问楼梯有多少种。
solution
简单的记忆化搜索,不需要高精度。
时间复杂度:\(O(n^2)\)
URAL 1023
题目描述:有\(n\)颗石子,有两个人进行游戏,轮流拿走石子,每次拿走的石子数目范围为\([1, m]\),拿走最后一颗的人算赢,请求出最小的\(m(m \geq 2)\),使得后手必胜。
solution
小学奥数题,显然\(n%(m+1)=0\)时,后手必胜,所以只要求\(n\)的最小因子即可,但要注意\((m \geq 2)\)的限制。
时间复杂度:\(O(\sqrt{n})\)
URAL 1024
题目描述:给出一个关于\(n\)排列的置换\(P\),问至少需要置换多少次才能变回\(1, 2, 3 ... n\)。(可以证明一定能回到\(1, 2, 3 ... n\))
solution
可以求出每个数至少需要置换多少次才能变回自己,也就是这个数的循环,然后求所有数的循环的最小公倍数就是答案。
时间复杂度:\(O(n^2)\)
URAL 1028
题目描述:给出平面上的\(n\)个点,记每个点的左下方的点的个数为该点的\(level\),问每个\(level\)有多少个点。
solution
数据已经排好序了,直接用树状数组就好了。
时间复杂度:\(O(nlogn)\)
URAL 1033
题目描述:给出一个展厅的平面图,‘.’是空地,‘#’是墙,展厅外围也是墙,左上角和右下角是入口,所以这两个格子有两面不是墙,现在要给能被游客看到的墙面贴上墙纸,问需要墙纸的面积。
solution
搜索。碰到墙壁就记一次数,或者搜索完后判断某一个面是否是能访问的空地与墙的交界。注意两个入口可能不连通。
时间复杂度:\(O(n^2)\)
URAL 1034
题目描述:一个\(n*n\)的棋盘上有\(n\)个皇后,这\(n\)个皇后两两不能攻击到对方,这时的局面称为peaceful, 问改变任意三个皇后的位置,使得局面依然是peaceful, peaceful的局面有多少个,注意:所有的皇后都看做是相同的。
solution
枚举三个皇后,改变他们的位置(只有两种情况),判断是否peaceful,判断方法与\(n\)皇后问题一样。
时间复杂度:\(O(n^3)\)



