期望值
期望值
这个星期恶补了一下期望值,感觉有些题目还是挺灵活的,只要方向正确,基本上都能把公式写出来。
论文《浅析竞赛中一类数学期望问题的解决》
期望值的基本公式
1、如果\(X\)是一个离散的随机变量,输出值为\(x_1, x_2, ...\) 和输出值相应的概率为\(p_1, p_2, ...\)(概率和为 1), 那么期望值\(E(X)=\sum_i p_ix_i\)
2、对于任意随机变量\(X,Y\)以及常量\(a,b\), \(E(aX+bY)=aE(X)+bE(Y)\)
3、档两个随机变量\(X,Y\)独立且各自都有一个期望时,有\(E(X \cap Y)=E(X)E(Y)\)
problems
聪聪与可可(NOI2005)
题目描述:有一个拥有\(n\)个点的无向图,聪聪和可可分别在一个点,可可每个时间单位都会选择去相邻的一个点或者不动(概率相等),而聪聪每个时间单位会走到可以缩短他们之间距离的点,如果有多个则选择编号最小的点,如果这时聪聪和可可不在同一个点,那么聪聪可以再走多一步而不花费时间,聪聪先走,求平均聪聪需要多长时间才能与可可在同一个点。
solution
先预处理出\(next[i][j]\),表示聪聪在\(i\), 可可在\(j\)时,聪聪下一步走哪里,还有每个点的度\(d[i]\)。设\(f[i][j]\)为当聪聪在\(i\),可可在\(j\)时的期望时间。则\((to[j][k])\)表示与\(j\)相连的第\(k\)个点。
\(f[i][i]=0, f[i][j]=1(if\) \(nid==j\) \(or\) \(next[i][j]==j)\)
记忆化搜索即可。
Highlander(SGU 385)
题目描述:随机给出\(1\)到\(n\), \(n\)个数字的一个错位排列 \(a\), 对应了一张有向图\(G = (V, E)\),其中\(V=\){\(1, 2, …,n\)}\(, E=\){\((i, a_i)\)}。问在最长环上的顶点数的期望值。
solution
首先,这些环都是简单环且没有自环。重要的是知道在\(m\)个数字中取出\(k\)个数字组成一个环有\(\frac{A_m^k}{k}\)种方案,如果有\(i\)个环长度相同,则需除以\(A_i^i\)。
设\(f[i][j][k]\)表示错位排列中\(i\)个数字已经确定,最长环为\(j\), 且有\(k\)个长度为\(j\)的环的方案数,为避免重复计算,设定环的长度递增不下降。
Red is good (TopCoder SRM420 Div1)
题目描述:有\(R\)张红牌和\(B\)张黑牌, 随机打乱然后一张一张地翻牌,翻到红牌得到 1 美元,黑牌则付出 1 美元。可以随时停止翻牌,在最优策略下平均能得到多少钱。
solution
用\(f[i][j]\)表示剩下\(i\)张红牌和\(j\)张黑牌获得钱的期望。
\(f[R][B]\)即为所求
收集邮票(bzoj1426)
题目描述:有n种不同的邮票,皮皮想收集所有种类的邮票。唯一的收集方法是到同学凡凡那里购买,每次只能买一张,并且买到的邮票究竟是n种邮票中的哪一种是等概率的,概率均为1/n。但是由于凡凡也很喜欢邮票,所以皮皮购买第k张邮票需要支付k元钱。 现在皮皮手中没有邮票,皮皮想知道自己得到所有种类的邮票需要花费的钱数目的期望。
solution
设\(f[i]\)表示现有\(i\)种邮票,期望还要买\(f[i]\)张,\(f[n]=0\)
\(f[i]=f[i]*\frac{i}{n}+f[i+1]*\frac{n-i}{n}+1\)
设\(g[i]\)表示现有\(i\)种邮票,期望还要\(g[i]\)元,\(g[n]=0\)
\(g[i]=(g[i]+f[i])*\frac{i}{n}+(f[i+1]+g[i+1])*\frac{n-i}{n}+1\)
买一张邮票时已经预支付了后面每张邮票各1元,所以可以看成当前邮票只是1元。\(g[0]\)即为答案。
tribbles(uva11021)
题目描述:一开始有\(n\)个球,每个球只活1天,在死之前,每个球有\(P_i\)(最多生\(s-1\)只)的概率生出\(i\)个球,问\(m\)天后全部死亡的概率。
solution
因为每个球都是独立的,所以只要算出一个球及其后代第\(m\)天全部死亡的概率\(f[m]\),答案就是\(f[m]^n\)
\(f[i]\)可理解为剩下\(i\)天全部死亡的概率,假如生了\(j\)个球,那么每个球在剩下的\(i-1\)天全部死亡的概率为\(f[i-1]\),\(j\)个球就是\(j\)次方。
取球游戏(bzoj4204)
题目描述:给出\(1\)到\(n\)的标号和\(m\)个球,每次随机取一个球,将其标号+1之后放回,如果取出的标号是\(n\)就置为\(1\),求执行\(k\)次操作之后每种球的期望个数。
solution
设\(f[i][j]\)表示第\(i\)次操作后,标号为\(j\)的球的期望个数
\(f[i][j]=(1-\frac{f[i-1][j]}{m})*f[i-1][j]+\frac{f[i-1][j]}{m}*(f[i-1][j]-1)+\frac{f[i-1][j-1]}{m}\)
\(=f[i-1][j]-\frac{f[i-1][j]}{m}+\frac{f[i-1][j-1]}{m}\)
因为\(k\)比较大,所以考虑用矩阵乘法,然后发现矩阵是一个循环矩阵,所以矩阵乘法可优化为\(O(n^2)\)
概率充电器(bzoj3566)
题目描述:给出一棵\(n\)个点的树,再给出每个点是电源的概率,每条边导电的概率,问期望有多少个点带电。
solution
这题求每个点带电的概率有点麻烦,而求每个点不带电的概率比较好算。设\(f[i]\)为第\(i\)个点由它的儿子影响下,不带电的概率,\(g[i]\)则表示由父亲影响。\(p_{ij}\)为\(i,j\)边的导电概率,\(q_i\)为\(i\)为电源的概率。
求\(g[i]\)的时候要求出\(i\)的父亲\(fa\)不导电的概率,这时要除去\(i\)对\(fa\)的影响。设\(tmp\)为除去\(i\)后\(fa\)不导电的概率,
注意判断\(tmp\)的分母是否为\(0\).
以上所讲的都是用递推式来求期望值,如果把这些递推式看成是一条条方程,在时间允许的条件下,也可以用高斯消元来求答案。
水水的例题
题目描述:给出一张图,给出每条边的长度,在一个点走到相邻的每个点的概率是相等的,问从\(1\)号点走到\(n\)号点的期望长度。
solution
如果这时无环有向图,那么就可以用递推式的方法来做,问题是这道题是无向有环图,只有对于每个点列出方程,然后用高斯消元求解。
First Knight(SWERC 2008 Problem B)
题目描述:给出一个\(n*m\)的矩形棋盘,给出每个格子走到相邻四个格子分别的概率(每个格子的不同),问从\((1, 1)\)走到\((n, m)\)的期望步数。
solution
貌似方程很容易就可以列出来,但数据范围是\(n,m \in [1, 40]\).\(O(n^3m^3)\)肯定过不了。但可以对高斯消元进行优化。
首先,让\((1, 1)\)这一未知数最后消元,这样就不用回代了。
接着,上图(取自《浅析竞赛中一类数学期望问题的解决方法》ppt)
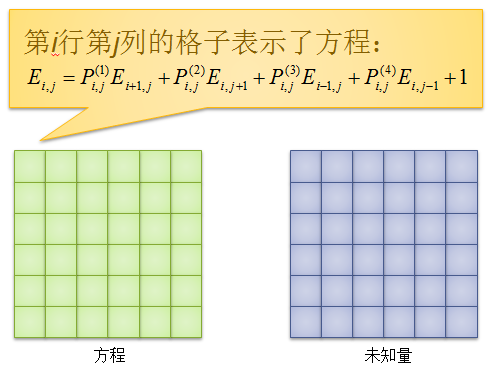
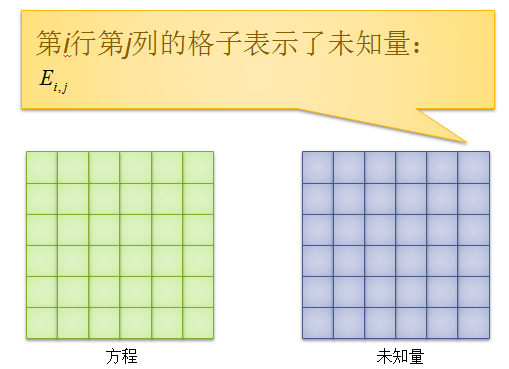
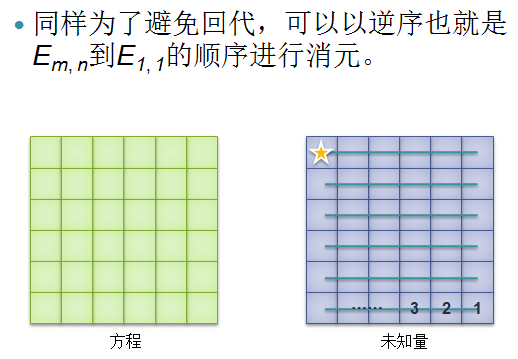
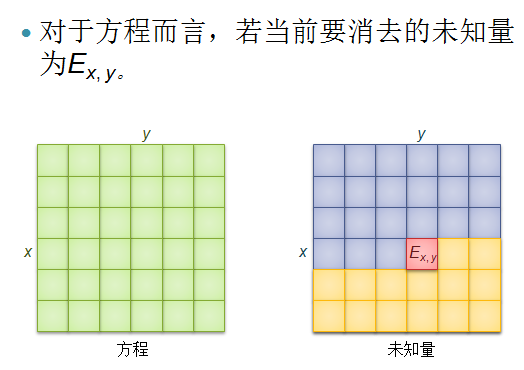
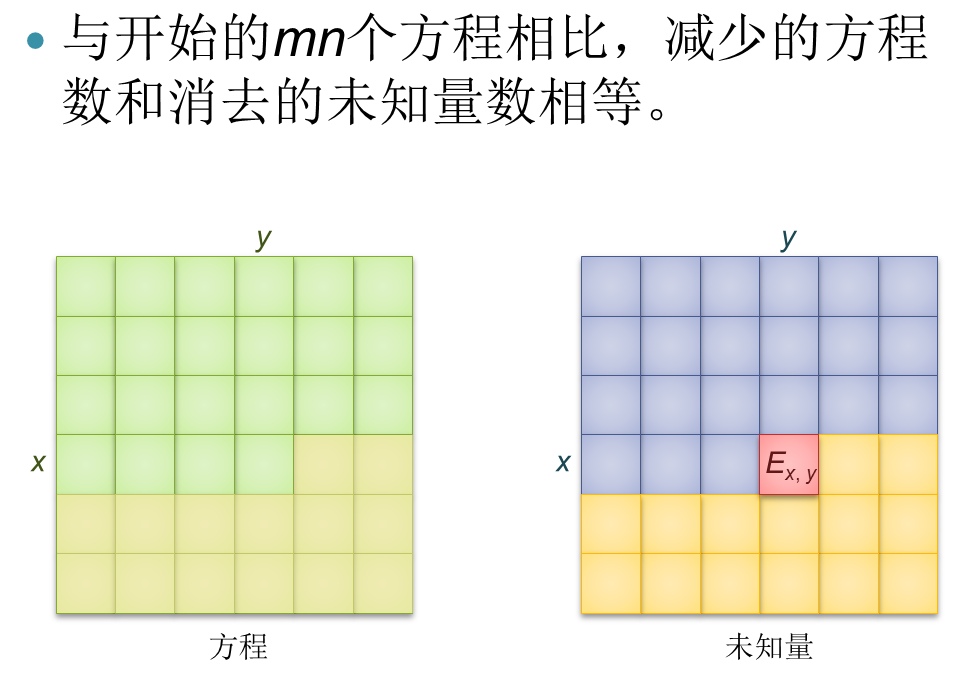
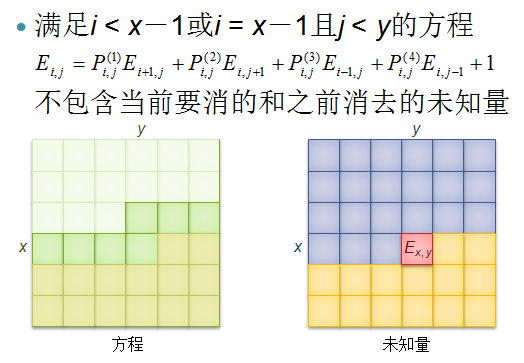
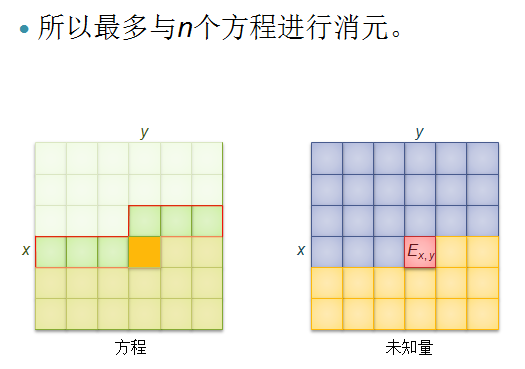
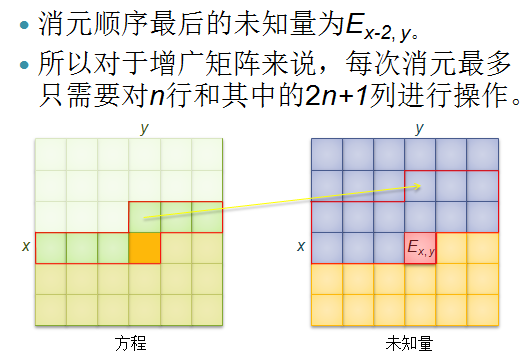
即与当前未知量有关的方程数只有\(m\)个,而这\(m\)的方程涉及的未知量只有\(2m+1\)个,所以最终的时间复杂度为\(O(nm^3)\)



