KMP 理解

例题

以字符串 ABABACA 为例

a
前缀：
后缀:

结果为0

ab
前缀：a
后缀: b

结果为0

aba
前缀：a ab
后缀: ba a

结果为1，此时 i＝2，j＝1

abab
前缀：a ab aba
后缀: bab ab b

结果为2，此时 i＝3，j＝2

ababa
前缀：a ab aba abab
后缀: baba aba ba a

结果为3，此时 i＝4，j＝3

ababac
前缀：a ab aba abab ababac
后缀: babac abac bac ac c

结果为0，此时 i＝5，j＝3，1，0

ababaca
前缀：a ab aba abab ababac ababaca
后缀: babaca abaca baca bac ac c

结果为1，此时 i＝6，j＝0

next数组结果：
0 0 0 1 2 3 0 1

总结

以i为尾，往前数对应值，即是相等的，前提是相等的情况下（废话！）；

前缀：要第一个字母，不要最后一个字母；
后缀：不要第一个字母，要最后一个字母；

至于i+1，因为计算的是前缀和后缀的重合的值的长度，所以还需要加上1；

最重要的是
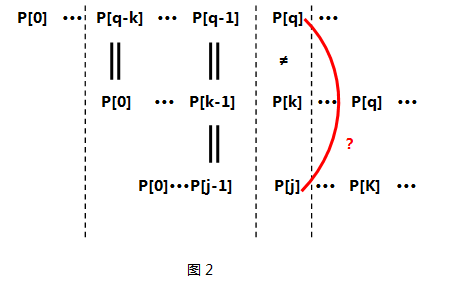
j = next[i - 1]，比如说现在在 i 位置上不匹配，为了避免重复匹配，不想浪费之前 0 到 i-1 的匹配长度，也就是说要找以 0 开头，i-1 结尾的匹配的子串，就是说找字符串上 i-1 位置的重合长度，因为next数组存储的是前缀和后缀的重合长度，所以还需要 i-1-1，也就是找next[i-1-1]的值，此时我们再比较字符串上 i 和 j 位置的字符是否相等；

如果相等 j 就尽管移动，代表重合的长度，也就是说到了该位置不匹配，只需要向前移动next数组中对应的长度。

贴上代码：

#include <iostream>
#include <string>
#include <vector>
using namespace std;

vector<int> getNext(string str) {
    int len = str.size();
    int j = 0;
    
    vector<int>next(len + 1);
    next[0] = next[1] = 0;
    
    // j表明相同的个数
    for (int i = 1; i < len; i++) {
        while (j > 0 && str[i] != str[j]) {
            j = next[j];
        }
        // 相同的个数
        if (str[i] == str[j]) {
            j++;
        }
        next[i+1] = j;
    }
    
    return next;
}

// 另一种写法
//    vector<int> getNext2(string str) {
//        int j = 0;
//        int i = 1;
//        
//        vector<int> next(str.size());
//        next[0] = 0; // 必须是0
//        
//        while (i < str.size()) {
//            if (str[i] == str[j]) {
//                j++;
//                next[i] = j;
//                i++;
//            }
//            else {
//                if (j != 0) {
//                    j = next[j - 1];
//                }
//                else { // j 为 0
//                    next[i] = 0;
//                    i++;
//                }
//            }
//        }
//        
//        return next;
//        
//    }


int search(string original, string find, vector<int> next) {
    int i = 0, j = 0;
    for (i = 0; i < original.length(); ++i) {
        while (j > 0 && original[i] != find[j]) {
            j = next[j];
        }
        if (original[i] == find[j])
            ++j;
        if (j == find.size()) {
            return i - j + 1;
        }
    }
    
    return -1;
}

int main(int argc, const char * argv[]) {
    string o = "ABABACAAC";
    string f = "ABABACA";
    
    vector<int> next = getNext(f);
    // next
    int i = 1;
    while (i < next.size()) {
        cout << "next " << next[i] << endl;
        i++;
    }
    
    //search
    int result = search(o, f, next);
    cout << "result " << result << endl;
    
    return 0;
}