题解-CF1508
连续被几个同学吊打 \(10\) 场了,这次总算抬了下头(很明显是运气因素,下次又要被吊打了)。
场切 A B C,补了 D E,F 放一放,要莫队(听说这东西只有东方神秘的中国 OIer 才会)。
贺了 D 和 E 两题的官方题面图片帮助理解题意。
CF1508A Binary Literature
神似某场 AGC 一道我场上做了约 \(100 \min\) 最终还是没有做出来的 A 题,但是简单得多。
把三个串分为 1 的个数 \(\ge n\) 和 0 的个数 \(\ge n\)(如果都满足就是前者好了)。
根据抽屉原理,很明显会有一个类有至少两个,不妨设为前者。
搞两个串中 1 的数量的最大值个 1,在相邻两个 1 之间塞两个串同个位置之间的 0 的数量的最大值个 0 即可(最左边的 1 左边和最右边的 1 右边同理)。
CF1508B Almost Sorted
双管齐下:先找个规律,发现长度为 \(n\) 的有 \(2 ^ {n - 1}\) 种。
然后总结一下这个排列的规律:发现 \(n\) 个数被划分成若干个区间 \([l, r)\),并且每个区间正好是 \([l, r)\) 这段连续的排列翻转过来(比如 \([3, 7)\) 这段区间就是 \(\{6, 5, 4, 3\}\))。
然后就可以用排列求字典序第 \(k\) 大的常见套路了,不过要便便。原来是依次枚举每个数,现在依次枚举每个区间。
然后还有一个小问题,就是 \(2 ^ {n - 1}\) 很可能爆 long long,如果这样直接搞成 \(2\times 10 ^ {18}\) 即可。
CF1508C Complete the MST
虽然做出来了,但是 \(6\) 发罚时让我错过回红!以后再也不用带 exit(0) 的调试语句了!
异或和为 \(0\) 很明显就是忽悠人的把戏,可以分为两种情况讨论:
- 没确定权值的边有 \(\ge n\) 条,那么至少一条边不用,所以可以用那条边平衡异或和,别的边边权都是 \(0\),实现的时候直接默认所有没有给出的边权值都是 \(0\) 即可。
- 否则 \(\frac{n(n - 1)}{2} - m < n\Longrightarrow m > \frac{n(n - 3)}{2}\)。那么 \(n \le 700\)。可以暴力。
然后讲讲上面两种情况的具体实现:
对于第一种,可以并查集和 stl::set 或者 FenwickTree 先把所有反图连通块给搞出来,然后用给定边在这个并查集上跑 Kruskal 即可。时间复杂度 \(\Theta((n + m)\log n)\)。
我用的是 FenwickTree,对于每个连通块,从一个任意点开始蔓延:
维护两个集合(stl::vector),一个是当前连通块所有点的出边交,另一个是当前连通块的所有点。
很明显两个集合没有交集,如果一个点不在它们的并集中,那么就可以加入当前连通块。
用 FenwickTree 维护两个集合的并集,可以用树状数组二分(\(\Theta(\log n)\))求出还有没有可以加入当前连通块的点以及如果有编号最小的这样的点是什么。
对于第二种,可以先用给定边跑一次 Kruskal 得出大小为 \(\Theta(n)\) 的有用边集。
然后对于每条未给定边(最多 \(n - 1\) 条),把他的权值改为所有给定边权值的异或和,然后把所有给定边和未给定边跑一次 Kruskal 然后求最小生成树权值最小值即可,时间复杂度 \(\Theta(m\log n)\)。
CF1508D Swap Pass
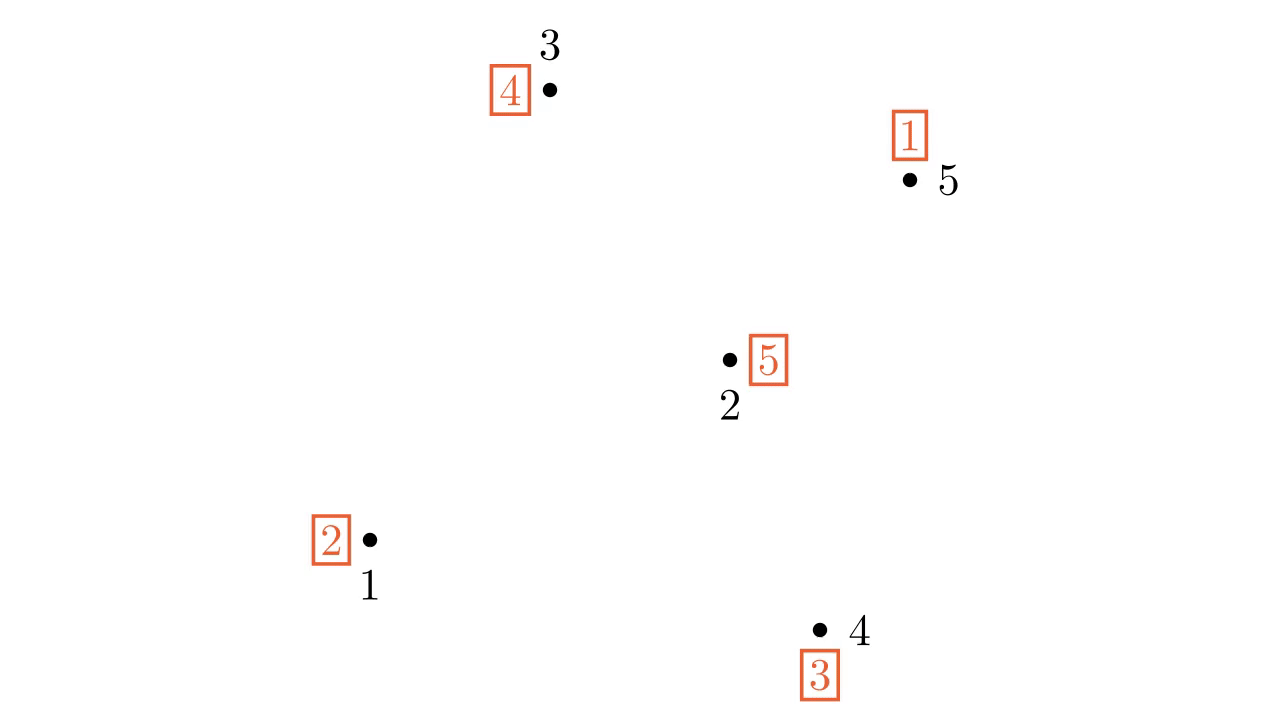
貌似每次这种交换两个恢复排列的题都是“必然有解,一个置换怎么做,多个置换怎么做”。
首先必然有解(可以先这么假设,然后下面给出构造),然后可以忽略 \(a_i = i\) 的所有 \(i\)。
然后考虑一个置换怎么做:随意选一个点,不停交换 \(a_i\) 和 \(a_{a_i}\) 直到 \(a_i = i\) 即可。
那能不能每个置换都这么做呢?由于置换不影响几何位置,所以这样可能会有两个置换之间的交换相交。
容易发现,如果交换两个来自不同置换的点,那么两个置换就合并了。
然后就是要开发脑洞再固定一个点当作原点,把别的点(\(a_i\neq i\))极角排序,设总共有 \(m\) 个点。
只交换极角排序相邻(包括首尾)且夹角 \(< \pi\)(这里我想了好久没想到,我果然对计算几何不熟悉啊!一个上午就这么没了)的两个点的至少可以有 \(m - 2\) 次交换,由于每个置换的点数 \(\ge 2\),易证只通过这些交换可以把所有置换合并,且交换不相交。
然后对于剩下的这 \(1\) 个置换,把选的原点当做选定点不停交换即可,易证没有交换相交。
CF1508E Tree Calendar
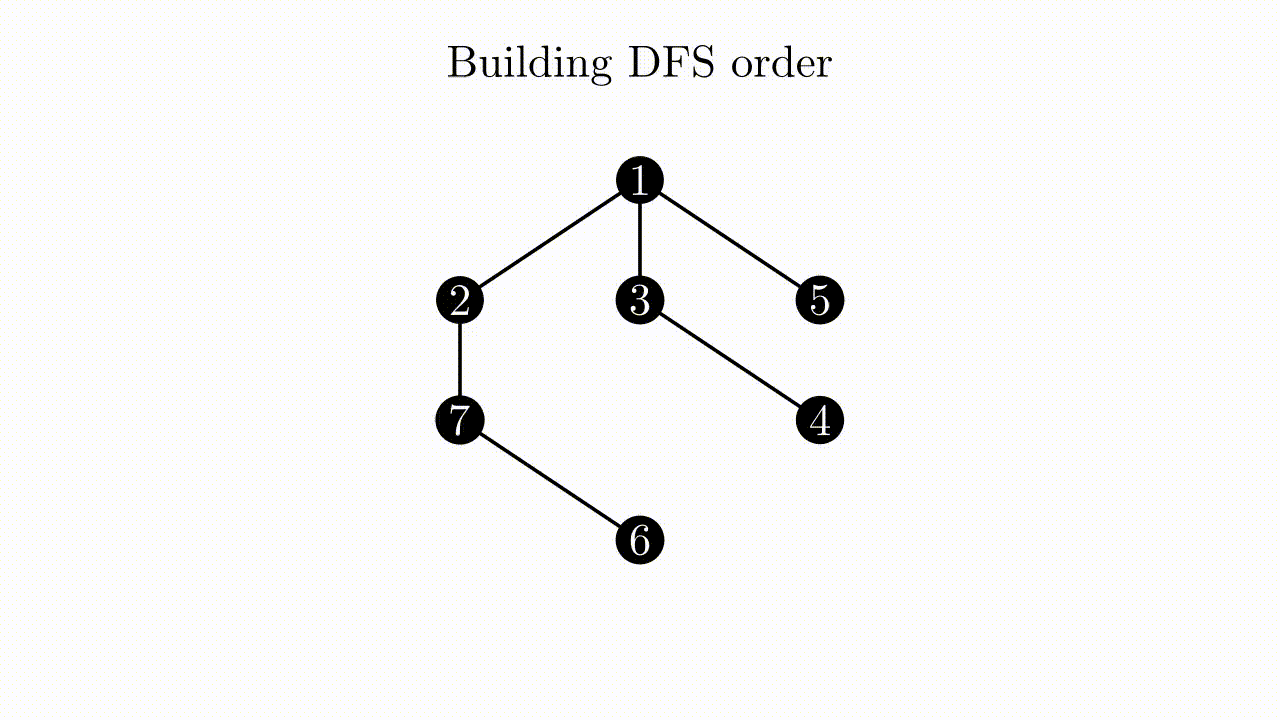
少看了“字典序最小”这个条件,我的一个下午啊(/wul/ll)。
那么对于一棵树的操作路径是固定的,且每个点 \(u\) 上的数都是往下移到一个子树顺序最小且极低的还没有标记的节点,然后标记这个节点。
观察最终的序列会发现新的序列是子树顺序和老的序列(入栈序)一样的树的出栈序。
而且很容易发现,对于任意一个节点,无论怎么操作,子节点(就是和它相连的点)上的数的相对大小都是不会变的(比如原来是 \(2, 3\),现在很可能就是 \(1, 3\) 或 \(1, 2\)),所以可以得出原树的子树顺序以及原序列。
然后开始处理得到的序列。如果根节点上的数是 \(x\),那么此时正在移动的必然是 \(x - 1\),可以先把 \(x - 1\) 恢复到根节点(不停和父亲节点上的数交换),这样就没有正在进行的移数流程了。这时候要判断原来 \(x - 1\) 要到的位置是不是在原来 \(x - 1\) 的位置的子树里,如果不是就 NO,否则当前问题就和原问题等价了。
否则,如果这个树的序列是合法的,那么所有 \(a_u < x - 1\) 的点 \(u\) 必然是移好的,否则必然是没移好的。只需要把移好的和出栈序对比,未移好的和剩下的树(删去移好节点)的入栈序对比即可。如果不同就输出 NO。否则就是 YES,移动次数是所有移好的的深度之和,要求的初始序列就是初始入栈序。


