题解-CF1491
场上进度:A B C D E,补题进度:G F。
中国场细节多,最近又因为 AFO 连续 \(10+\) 天没写代码,比赛前也没 VP 回复过状态,只做了两三天的题(主要在划水),然后就狂暴罚时……祝贺自己成为同学中分最低的 /kk。
\(*x\) 表示我 unaccepted 了 \(x\) 发。总共:\(*9\),赛时 \(*8\)。
A K-th Largest Value
维护 \(1\) 的个数即可。\(*0\)。
const int xn = 1e5;
int n, m, a[xn], cnt;
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m;
rep(i, 0, n) cin >> a[i], cnt += a[i];
while (m--) {
int o, i; cin >> o >> i, --o, --i;
if (o) cout << (i < cnt) << '\n';
else cnt -= a[i], a[i] ^= 1, cnt += a[i];
}
return 0;
}
B Minimal Cost
- 如果所有 \(a_i\) 相等:那么一发左右移必须,然后可以上下或左右。
- 如果所有 \(a_i\) 和 \(a_{i + 1}\) 的差最大为 \(1\),那么只需要一发左右或上下移。
- 否则,答案为 \(0\)。
\(*1\):我忘了第三种情况,这就离谱。
const int xn = 100;
int n, u, v, a[xn];
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int cas; cin >> cas;
while (cas--) {
cin >> n >> u >> v;
bool same = true, ok = false;
rep(i, 0, n) cin >> a[i];
rep(i, 0, n - 1) {
same &= a[i] == a[i + 1];
ok |= abs(a[i] - a[i + 1]) > 1;
}
int res = inf32;
if (same) res = v + min(u, v);
else if (ok) res = 0;
else res = min(u, v);
cout << res << '\n';
}
return 0;
}
C Pekora and Trampoline
场上直接写了 \(\Theta(n)\) 的做法。
从左到右处理,设 \(b_i\) 表示到 \(i\) 这里有 \(b_i\) 次免费跳跃机会,初始为 \(0\)。
设处理到 \(i\),那么有 \(\max(0, a_i - 1 - b_i)\) 次跳跃要付费。
由于 \(i + 2\sim i + a_i\) 必然会跳到一次,所以这段 \(b\) 集体加一,可以差分实现。
然后因为有些时候免费跳跃次数过多,所以 \(i + 1\) 还会被跳到 \(\max(0, b_i - (a_i - 1))\) 次。
\(*4\):打成了 \(n^3\) 暴力(还循环写错了一发),开始差分(没考虑到跳 \(i + 1\),\(b\) 数组没清零)。
const int xn = 5000;
int n, a[xn], b[xn];
void add(int i, int x) {if (i < n) b[i] += x;}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int cas; cin >> cas;
while (cas--) {
cin >> n;
i64 res = 0;
rep(i, 0, n) cin >> a[i], b[i] = 0;
rep(i, 0, n) {
if (i) b[i] += b[i - 1];
res += max(0, a[i] - 1 - b[i]);
add(i + 1, max(0, b[i] - (a[i] - 1)));
add(i + 2, 1 - max(0, b[i] - (a[i] - 1)));
add(i + a[i] + 1, -1);
}
cout << res << '\n';
}
return 0;
}
D Zookeeper and The Infinite Zoo
就是你手上有一个数 \(s\),每次可以找一个 \(v\in s\) 并让 \(s += v\),问最后能不能变成 \(t\)。
如果 \(s > t\) 直接不能,否则可以发现 \(s\) 的任意一个低位缀,\(1\) 的个数都不会增加。
而只要每个低位缀 \(s\) 不比 \(t\) \(1\) 少,就有解(这个操作很灵活,可以随意消 \(1\),把一段 \(1\) 集体高移)。
\(*2\):打表打错了找出了错规律,又写出了错的贪心。
bool check(int u, int v) {
if (u > v) return false;
int uc = 0, vc = 0;
rep(i, 0, 30) {
if (u >> i & 1) ++uc;
if (v >> i & 1) ++vc;
if (uc < vc) return false;
}
return true;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int cas; cin >> cas;
while (cas--) {
int x, y;
cin >> x >> y;
if (check(x, y)) cout << "YES\n";
else cout << "NO\n";
}
return 0;
}
E Fib-tree
先判是否存在 \(n = fib_k\),听说不判会 FST。
由于 \(k - 1\) 级子树必过重心,所以 \(k - 2\) 级子树是重心为根的两个子树,所以最多有 \(2\) 种符合数量的分法。
需要证明,如果整棵树是有解的,两种分法是等价的:
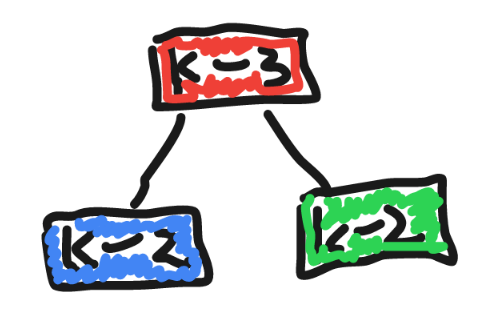
如果有 \(2\) 种分法,树结构必然如下(重心在红块里):
由于 \(k \le 3, n \le 3\) 都有解,所以如果 \(k \le 5, n \le 8\),这个结论必然成立。
那么可以假设对于树级 \(i \in [0, k)\),我们已经证明这个结论成立。
那么无论分左边还是分右边,把 \(k - 1\) 级子树再分后都和两条边同时割等价。
所以对于树级 \(k\) 结论成立,递推得对于所有树级 \(i\) 结论成立。
那么每次 \(\Theta(fib_k)\) 找边然后分治即可,时间复杂度 \(\Theta(n\log n)\)。
\(*2\):找边找漏了,全局变量在递归中修改然后出来后调用导致出错。
const int xn = 2e5 + 1, xf = 27;
int n, fib[xf], id[xn];
void init() {
fib[0] = fib[1] = 1;
rep(i, 2, xn + 1) id[i] = -1;
rep(i, 2, xf){
fib[i] = fib[i - 1] + fib[i - 2];
id[fib[i]] = i;
}
}
vector<int> adj[xn];
bool vis[xn];
int si[xn], eu, ev, k;
void finde(int u, int fa) {
si[u] = 1;
for (int v : adj[u]) {
if (vis[v] or v == fa) continue;
finde(v, u), si[u] += si[v];
}
if (si[u] == fib[k - 2] and !~eu) eu = u, ev = fa;
if (si[u] == fib[k - 1] and !~eu) eu = fa, ev = u;
}
bool dfs(int u) {
if (k <= 3) return true;
eu = -1, ev = -1, finde(u, -1); int a = eu, b = ev;
if (!~eu) return false;
bool res = true;
vis[a] = true, --k, res &= dfs(b), vis[a] = false, ++k;
vis[b] = true, k -= 2, res &= dfs(a), vis[b] = false, k += 2;
return res;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
init(), cin >> n;
rep(i, 0, n - 1) {
int u, v; cin >> u >> v, --u, --v;
adj[u].push_back(v), adj[v].push_back(u);
}
if (n <= 2) return cout << "YES\n", 0;
if (!~id[n]) return cout << "NO\n", 0;
if (k = id[n], dfs(0)) cout << "YES\n";
else cout << "NO\n";
return 0;
}
F Magnets
先化一下式子:\(F = (n_1 - s_1)(n_2 - s_2)\)。
很明显如果得到了一个有磁性的磁铁,把它和别的比较一下次数 \(n - 1\)。
可是这个东西并不能直接二分,所以只能一个一个枚举。
这里需要注意:一个一个枚举,只要让枚举失败也对答案也有贡献,就不会崩盘。
题目还说绝对值 \(\le n\),这也很有提示性,说明需要 \(\Theta(n)\) 个和 \(1\) 个为一组的查询。
所以可以从左到右,每次把 \(1 \sim i - 1\) 和 \(i\) 查询一下。
那么当 \(i\) 是第二颗有磁性的石头的时候,第一次 \(F \neq 0\)。
这时候 \(1 \sim i - 1\) 有恰好一颗磁石,正好可以利用 \(i\) 二分。
然后 \(i + 1 \sim n\) 每个都可以用 \(1\) 次查询得知是否有磁性。
操作次数最多为 \(n - 1 + \lceil\log_2 n\rceil \le n + \lfloor\log_2 n\rfloor\)。
时间复杂度 \(\Theta(n^2)\)。
\(*0\):Good job!
const int N = 2000;
int n, F, nd, d[N];
void Solve() {
cin >> n, nd = 0;
int s = -1;
rep(i, 1, n) {
cout << "? 1 " << i << '\n';
cout << i + 1 << '\n';
rep(j, 0, i) cout << j + 1 << ' ';
cout << endl;
cin >> F;
if (F) {
s = i;
break;
}
}
int l = 0, r = s;
while (r - l > 1) {
int mid = (l + r) / 2;
cout << "? 1 " << mid - l << '\n';
cout << s + 1 << '\n';
rep(i, l, mid) cout << i + 1 << ' ';
cout << endl;
cin >> F;
if (F) r = mid;
else l = mid;
}
rep(i, 0, l) d[nd++] = i;
rep(i, l + 1, s) d[nd++] = i;
rep(i, s + 1, n) {
cout << "? 1 1\n";
cout << i + 1 << '\n';
cout << s + 1 << endl;
cin >> F;
if (!F) d[nd++] = i;
}
cout << "! " << nd << ' ';
rep(i, 0, nd) cout << d[i] + 1 << ' ';
cout << endl;
}
G Switch and Flip
先转化为一张 \(n\) 个点由 \((i, p_i)\) 构成的有向图。
设正面朝上的点是红的,否则是蓝的,一次操作交换两个点的出点并翻转 \(2\) 个出点的颜色。
然后这题巧妙的地方就在于把两个环一起消比单独消一个环更优。
- 两个长度为 \(a, b\) 的环消掉耗费 \(a + b\) 步。
- 一个长度为 \(a > 2 : a\) 的环自己消掉耗费 \(a + 1\) 步。
具体操作(点击展开五彩斑斓的图图 /se)。
/se)。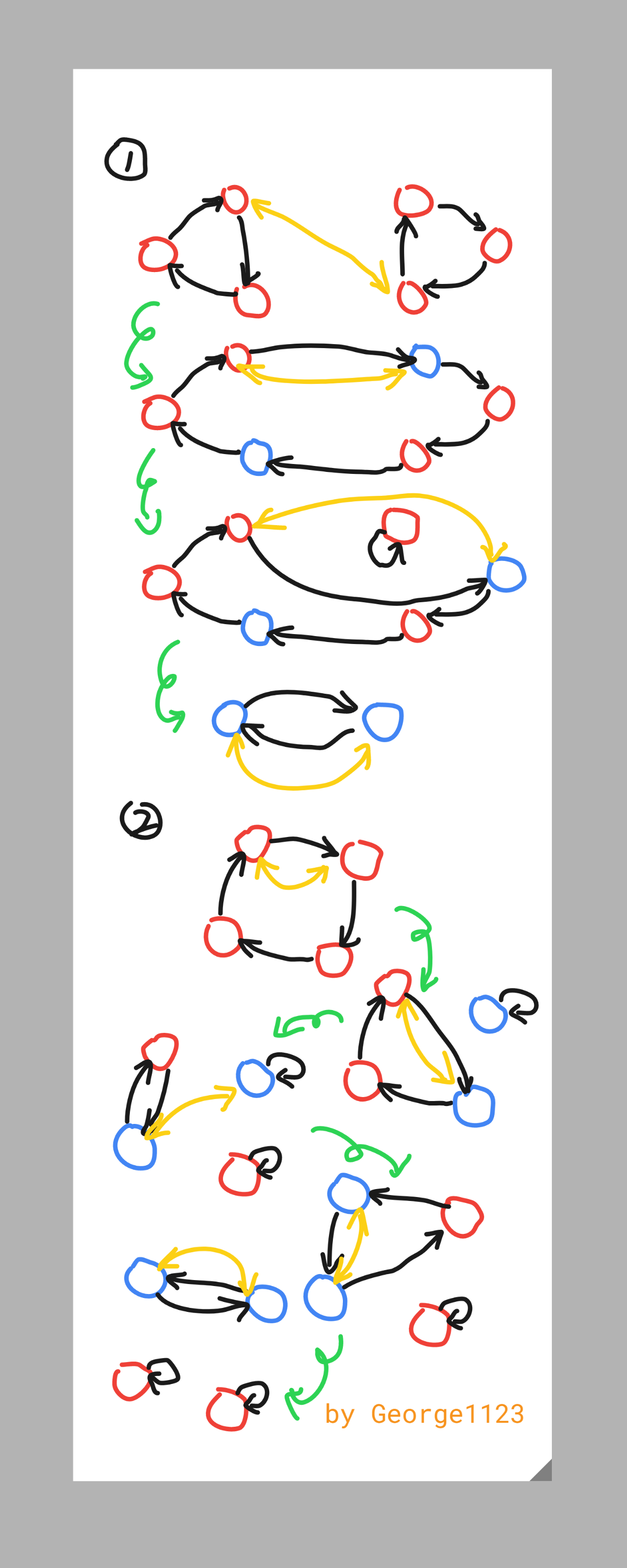
所以可以用 1 消得至多只剩一个环。
如果这个环有两个点,那么必然有不在这个环中的点,可以把这个环和那个点合并共 \(n + 1\) 步。
否则用 2 把这个环消掉即可。
\(*1\):把上文加粗部分看成了这两个点本身翻转颜色,然后做了一遍。
const int xn = 2e5 + 1;
int n, p[xn], q[xn], no, o[xn][2];
bool vis[xn];
void flip(int i, int j) {
swap(p[i], p[j]), swap(q[p[i]], q[p[j]]);
o[no][0] = i, o[no][1] = j, ++no;
}
void offset(int i, int j) {
flip(i, j), i = p[i], j = p[j];
while (p[i] != j) i = p[i], flip(q[i], q[q[i]]);
while (p[j] != i) j = p[j], flip(q[j], q[q[j]]);
flip(i, j);
}
void solone(int k) {
rep(i, 0, n) if (i == p[i]) return offset(i, k);
int i = k; k = p[k], flip(q[k], q[q[k]]);
while (p[k] != q[k]) k = p[k], flip(q[k], q[q[k]]);
flip(i, k), flip(k, q[k]), flip(i, p[i]);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n;
rep(i, 0, n) cin >> p[i], q[--p[i]] = i;
int k = -1;
rep(i, 0, n) if (not vis[i]) {
if (p[i] == i) continue;
while (not vis[i]) vis[i] = true, i = p[i];
if (!~k) k = i;
else offset(i, k), k = -1;
}
if (~k) solone(k);
cout << no << '\n';
rep(i, 0, no) cout << o[i][0] + 1
<< ' ' << o[i][1] + 1 << '\n';
return 0;
}
H Yuezheng Ling and Dynamic Tree
I Ruler Of The Zoo
濒临退役。