题解-AGC010
AGC010B Boxes
入手点：每次操作的和是固定正整数，所以可以知道操作次数。
然后看看两个相邻的数之间的差 \(\bmod n\) 是否符合这个操作次数。
然后可以得出两个相邻数之间的 \(n\to 1\) 断层次数，必须是非负整数，而且和必须为操作次数。
AGC010C Cleaning
对于每个节点，它的每个子树连接到它的路径数为 \(last_v\)。
然后子树内的 \(last\) 要么互相抵消，要么继续连接到父亲。
设子树中两个 \(x\) 互相抵消，\(y\) 继续连到父亲，\(last_v\) 的和为 \(sm\)，\(last_v\) 的最大值为 \(mx\)。
然后要判断每个节点的特殊情况，特判根和叶子节点（看代码）。
AGC010D Decrementing
如果已经有 \(1\) 了，就不能再 gcd 了，所以直接如果剩下偶数个数是奇数就先手获胜，否则是后手获胜。
注意到当有全局除 GCD 时，对答案有影响的是 \(2\) 这个因子。
如果当前有奇数个偶数，先手赢了，他只要不停取偶数，偶数就不会增多到把 \(2\) 的因子都消掉。如果大家一起除一个奇数，相当于没有除。
如果当前有偶数个偶数并且有超过一个奇数，后手赢了，同理。
否则就是偶数 \(n-1\) 个偶数的情况，如果先手取了偶数后手就赢了，所以取奇数。
然后所有数除以它们的 \(\gcd\)，递归判断即可。
AGC010E Rearranging
刚开始这题想不懂，后来和 WAPER 讨论了一下大概明白了。
对于不互质的数之间连一条边，然后形成一个竞赛图。
先手的目的是给竞赛图定向，因为不互质的数相对位置不会改变。
然后后手就是给一个不一定联通的 DAG 求一个最大的拓扑序。
先手的策略是对每个联通块 dfs，每次找到最小的没遍历的点，然后从当前点向该点连边，再忽略除了生成树以外的边，即：
bool vis[N],ir[N],e[N][N];
vector<int> adj[N];
void dfs(int u){
vis[u]=true;
R(v,n)if(!vis[v]&&e[u][v])
adj[u].pb(v),dfs(v);
}
// ...
R(u,n)if(!vis[u]) ir[u]=vis[u]=true,dfs(u);
这么操作的证明大部分题解都没有讲清楚，我是这么理解的，对于一个联通块，比如这只鱼：
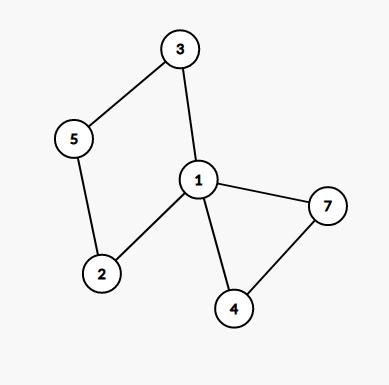
肯定得把 \(1\) 放在第一位，那么先把它当作根节点，假设我们已经知道要给一棵生成树定向。
然后下面有两个子树一样的东西，分别是 \(\{2,5,3\}\) 和 \(\{4,7\}\)。
两部分的定向互相没有影响，所以能做的只有让一个子树内最优。
那么当下的目的应该是让 \(2\) 在 \(\{3,5\}\) 之前。
因为这是个联通块，所以这一定是可能的。又因为只需要定向一棵生成树，所以 \(\{3,5\}\) 必须连在 \(2\) 后面（如果连在 \(1\) 后面就不能连在 \(2\) 后面了，然后 \(\{3,5\}\) 就可能被后手捣到 \(2\) 前面去）。
然后再对 \(\{3,5\}\) 这个子图内部定向，也同理，这里可以利用一个递归定向的思想。
然后最后还有一个问题：为什么要定向一个生成树。
假如我们已经定向好了一棵生成树，那么内部的边定向必然是最优的了。对于非树边，如果它是返祖边，那么它必须顺着树边方向（它不允许构成环）；否则它是某个节点下联通两个子树的边，它没被 dfs 选中说明它的定向不会更优，它只需要顺从敌人的意志即可。这样总是不会产生环的。
AGC010F Tree Game
这是单堆的问题，考虑用 P/N 态，先找必败态。
发现如果一个石头 $\le $ 所有相邻点的石头，无论棋子移到哪里，对手把棋子移回来就败了。
拓展一下，发现所有点不能往点权 \(\ge\) 自己的点走。
从 P/N 态角度，一定是从小的点权的P/N 态推到相邻的大的点权。
把树转化为 DAG，拓扑排序同时 dp 求出 01SG 值即可。
