题解-洛谷P4724 【模板】三维凸包
给出空间中 \(n\) 个点 \(p_i\),求凸包表面积。
数据范围:\(1\le n\le 2000\)。
这篇题解因为是世界上最逊的人写的,所以也会有求凸包体积的讲解。
三位向量的运算
-
模长: 即向量长度,\(|\vec{a}|=\sqrt{x_a^2+y_a^2+z_a^2}\)。
-
点积: 标量 \(\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos<\vec{a},\vec{b}>=x_ax_b+y_ay_b+z_az_b\),为 \(\vec{a}\) 的模长乘以 \(\vec{b}\) 在 \(\vec{a}\) 上的投影的模长。
-
叉积: 向量 \(\vec{a}*\vec{b}=(y_az_b-z_ay_b,z_ax_b-x_az_b,x_ay_b-y_ax_b)\),模长为平四面积。
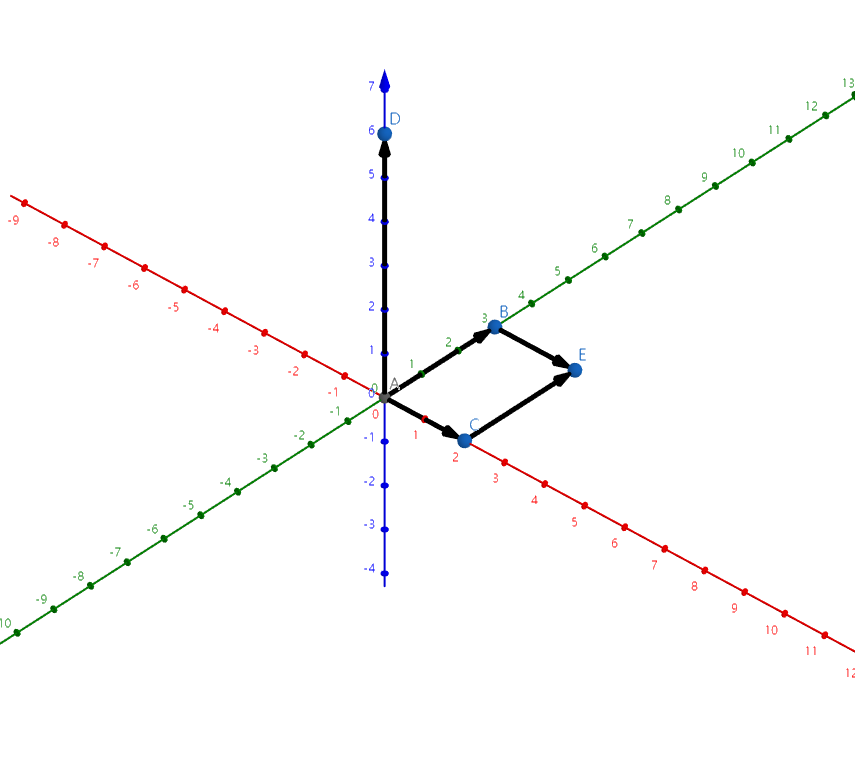
上图 \(\vec{AC}*\vec{AB}=\vec{AD}\),\(\vec{AD}\) 垂直 \(\vec{AC}\) 与 \(\vec{AB}\) 的平面,模长为平四面积。
会用到的计算与判定
- 判断点 \(E\) 在平面 \(ABC\) 上方:
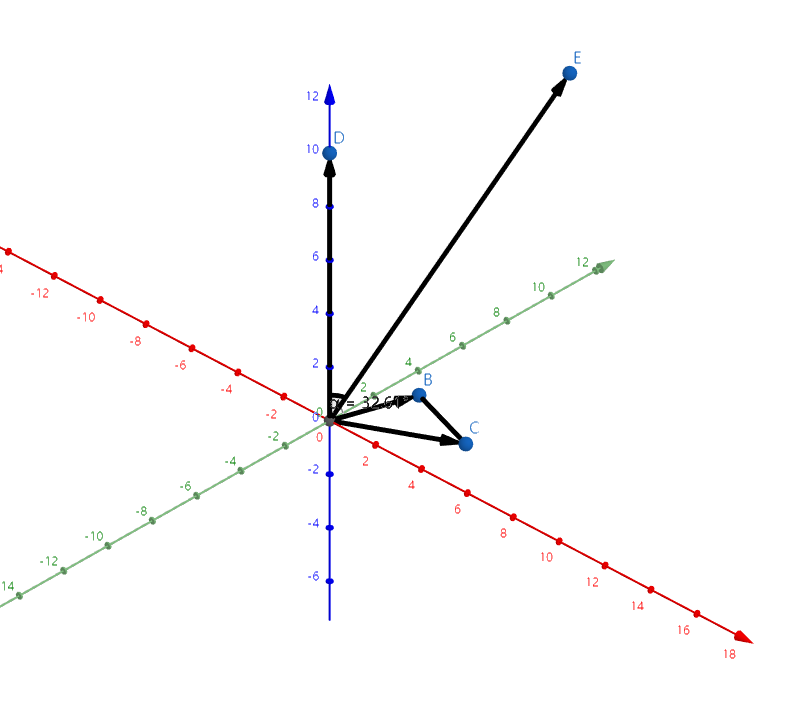
作 \(\vec{AD}=\vec{AC}*\vec{AB}\),用 \(\vec{AE}\cdot \vec{AD}>0\) 来判断 \(\angle DAE<\frac{\pi}{2}\)。
- 求点 \(E\) 到平面 \(ABC\) 的距离:
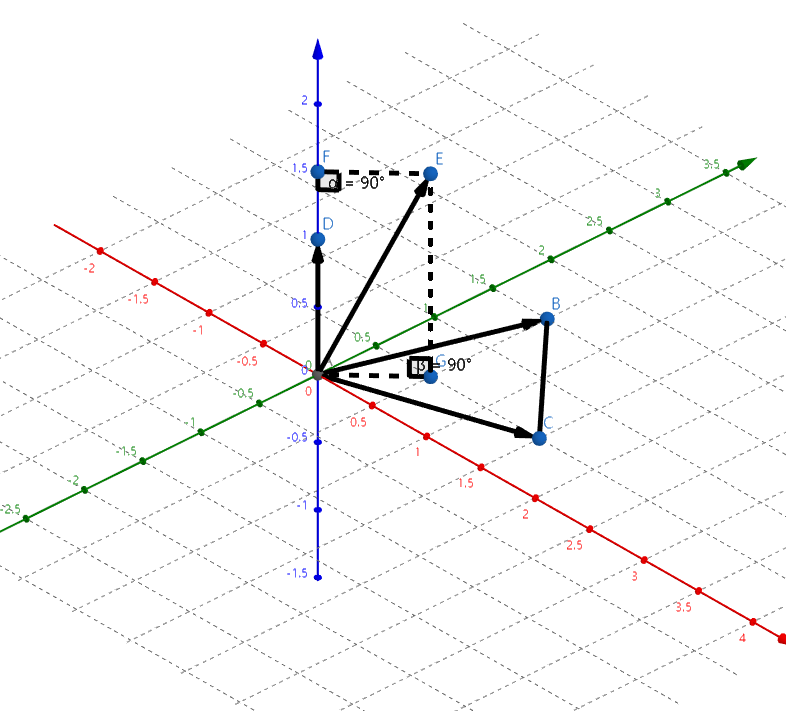
距离 \({\rm dist}(E,\triangle ABC)=EG=AF=\frac{\vec{AD}\cdot \vec{AE}}{|\vec{AD}|}=\frac{\vec{AD}\cdot \vec{AE}}{|\vec{AC}*\vec{AB}|}\)。
处理凸包
设凸包为 \(Con\),用逆时针顺序三个点表示一个三角形面。
每加入一个新点 \(p_{new}\) 的时候,把它当作光源照向之前的凸包,将未照到的面留下,加上 \(p_{new}\) 和光影边缘形成的新面。
引用巨佬的图:
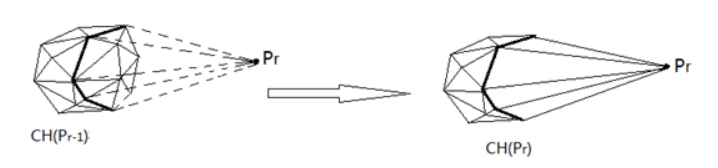
判断照不照得到用判定“点 \(E\) 在平面 \(ABC\) 上方”的方法。
判断光影边缘用 \(vis\) 数组。\(vis_{i,j}\) 表示 \((i,j,k)\)(即 \((i,j)\) 逆时针方向上的面)这个面是否照光,如果 \([vis_{i,j}=1]\&\&[vis_{j,i}=0]\),说明 \((i,j)\) 是光影边缘,需加面 \((i,j,p_{new})\)。
重复加点,得到 \(m\) 个 \(Con\) 上的面 \(f_i=(A,C,B)\)。
其中 \(D\) 是一个定点,需要在 \(Con\) 内或表面上,可以选 \(p_1\),上面是三棱锥体积计算公式。
时间复杂度 \(\Theta(n^2)\),空间复杂度 \(\Theta(n^2)\)。
每加入一个点,面最多增加 \(2\) 个。
证明:设光影边缘上有 \(n\) 个点,因为每个面是三角形,所以要去掉的面 \(\ge n-2\)(中间可能有点),增加的面数为 \(n\),所以增加的点数 \(\le 2\)。
代码
- 求表面积
#include <bits/stdc++.h>
using namespace std;
//Start
typedef long long ll;
typedef double db;
#define mp(a,b) make_pair(a,b)
#define x first
#define y second
#define be(a) a.begin()
#define en(a) a.end()
#define sz(a) int((a).size())
#define pb(a) push_back(a)
const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;
//Data
const int N=2000;
const db eps=1e-9;
int n,m;
db ans;
//Convex
mt19937 orz(time(0));
db reps(){return (1.*(orz()%98)/97-.5)*eps;}
struct point{
db x,y,z;
void shake(){x+=reps(),y+=reps(),z+=reps();}
db len(){return sqrt(x*x+y*y+z*z);}
point operator-(point p){return (point){x-p.x,y-p.y,z-p.z};}
point operator*(point p){return (point){y*p.z-p.y*z,z*p.x-p.z*x,x*p.y-p.x*y};}
db operator^(point p){return x*p.x+y*p.y+z*p.z;}
}a[N];
struct plane{
int v[3];
point flag(){return (a[v[1]]-a[v[0]])*(a[v[2]]-a[v[0]]);}
db area(){return flag().len()/2;}
int see(point p){return ((p-a[v[0]])^flag())>0;}
}f[N],g[N];
int vis[N][N];
void Convex(){
#define ft f[j].v[t]
#define bk f[j].v[(t+1)%3]
f[m++]=(plane){0,1,2},f[m++]=(plane){2,1,0};
for(int i=3;i<n;i++){
int cnt=0,b;
for(int j=0;j<m;j++){
if(!(b=f[j].see(a[i]))) g[cnt++]=f[j];
for(int t=0;t<3;t++) vis[ft][bk]=b;
}
for(int j=0;j<m;j++)
for(int t=0;t<3;t++)
if(vis[ft][bk]&&!vis[bk][ft]) g[cnt++]=(plane){ft,bk,i};
m=cnt;
for(int j=0;j<m;j++) f[j]=g[j];
}
}
//Main
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=0;i<n;i++) cin>>a[i].x>>a[i].y>>a[i].z,a[i].shake();
Convex();
for(int i=0;i<m;i++) ans+=f[i].area();
cout.precision(3);
cout<<fixed<<ans<<'\n';
return 0;
}
- 求体积
#include <bits/stdc++.h>
using namespace std;
//Start
typedef long long ll;
typedef double db;
#define mp(a,b) make_pair(a,b)
#define x first
#define y second
#define be(a) a.begin()
#define en(a) a.end()
#define sz(a) int((a).size())
#define pb(a) push_back(a)
const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;
//Data
const int N=2000;
const db eps=1e-9;
int n,m;
db ans;
//Convex
mt19937 orz(time(0));
db reps(){return (1.*(orz()%98)/97-.5)*eps;}
struct point{
db x,y,z;
void shake(){x+=reps(),y+=reps(),z+=reps();}
db len(){return sqrt(x*x+y*y+z*z);}
point operator-(point p){return (point){x-p.x,y-p.y,z-p.z};}
point operator*(point p){return (point){y*p.z-p.y*z,z*p.x-p.z*x,x*p.y-p.x*y};}
db operator^(point p){return x*p.x+y*p.y+z*p.z;}
}a[N];
struct plane{
int v[3];
point flag(){return (a[v[1]]-a[v[0]])*(a[v[2]]-a[v[0]]);}
db area(){return flag().len()/2;}
db dist(point p){return fabs(((p-a[v[0]])^flag())/flag().len());}
int see(point p){return ((p-a[v[0]])^flag())>0;}
}f[N],g[N];
int vis[N][N];
void Convex(){
#define ft f[j].v[t]
#define bk f[j].v[(t+1)%3]
f[m++]=(plane){0,1,2},f[m++]=(plane){2,1,0};
for(int i=3;i<n;i++){
int cnt=0,b;
for(int j=0;j<m;j++){
if(!(b=f[j].see(a[i]))) g[cnt++]=f[j];
for(int t=0;t<3;t++) vis[ft][bk]=b;
}
for(int j=0;j<m;j++)
for(int t=0;t<3;t++)
if(vis[ft][bk]&&!vis[bk][ft]) g[cnt++]=(plane){ft,bk,i};
m=cnt;
for(int j=0;j<m;j++) f[j]=g[j];
}
}
//Main
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=0;i<n;i++) cin>>a[i].x>>a[i].y>>a[i].z,a[i].shake();
Convex();
for(int i=0;i<m;i++) ans+=f[i].area()*f[i].dist(a[0])/3;
cout.precision(2);
cout<<fixed<<ans<<'\n';
return 0;
}
祝大家学习愉快!

