线性基
先普及一些异或的性质:
线性基
\(\texttt{OI}\) 中的线性基即异或线性基,属于一种算法或数据结构。异或线性基可以解决序列子集的异或和问题,常用于出思维题。
定义
对于一个序列 \(a_i(1\le i\le n)\),它的线性基为序列 \(lb_j(1\le j\le c,c=\log_2{\rm max}A)\),\(lb_j\) 和 \(a_i\) 的子集异或和集相等。
\(lb_j\) 是序列 \(a_i\) 的一个子集的异或和,并且该异或和的最高位 \(1\) 是 \(2^j\)。
如果不存在一个子集使得异或和的最高位 \(1\) 是 \(2^j\),\(lb_j=0\)。
一个序列的线性基可以有很多种。
如序列
的线性基可以是
。其中 \(lb_1=2=5\oplus 7\),不存在序列 \(a_i\) 的子集使异或和的最高位 \(1\) 为 \(2^0\)。
操作
插入
线性基的构造是通过插入数 \(x\) 来实现的。每次插入 \(\Theta(\log {\rm max}A)\)。
具体实现方法是逆序遍历数 \(x\) 为 \(1\) 的二进制位 \(j\):
如果该位有线性基(即 \(lb_j\not=0\)),令 \(x=x\oplus lb_j\),以消除 \(x\) 的 \(j\) 位,让 \(x\) 继续去找属于自己的一位。
如果该位没线性基(即 \(lb_j=0\)),令 \(lb_j=x\),此时 \(x\) 已经异或了不少 \(lb_k(j<k\le\log{\rm max}A)\) 了,他的实质是序列 \(a_i\) 自己的一个异或和。
代码:
//LB
const int LOGA=50;
ll lb[LOGA+7];
void add(ll x){
for(int i=LOGA;i>=0;i--)if(x>>i){
if(lb[i]) x^=lb[i];
else return void(lb[i]=x);
}
//很明显,一个数可能没有插入任何位置,然后就会跑到这里
}
查询
- 最大子集异或和
这里的最大子集异或和既可以是序列本身的最大子集异或和,又可以是在子集异或和异或一个数 \(x\) 的条件下的最大异或和。
如果是前者,初始化 \(res=0\);如果是后者,初始化 \(res=x\)。
同样是逆序遍历二进制位,如果 \(res\oplus lb_j>res\),就令 \(res=res\oplus lb_j\)。
为什么这样的贪心思想是正确的?可以想象每一个新异或上的 \(lb_j\) 都是不可能覆盖之前异或了的高位的,所以这是个没有后效性的贪心,所以是正确的。
代码:
int findmax(int x){
int res=x;
for(int i=LOGA;i>=0;i--)if((res^lb[i])>res) res^=lb[i];
return res;
}
- 子集异或和是否可以等于一个数
例题:Codeforces959F Mahmoud and Ehab and yet another xor task
有点像反插入。逆序遍历 \(x\) 为 \(1\) 的二进制位 \(j\):
如果有线性基,就令 \(x=x\oplus lb_j\) 以抵消 \(x\) 的 \(j\) 位,应用了
\[x\oplus lb_j=\bigoplus_{i\in xset}i\oplus a_i(lb_j=a_i,\bigoplus_{i\in xset}i=x,xset\in a) \]的引理(说了好像和没说一样)。
如果没线性基,说明子集异或和不可以等于 \(x\)。
代码:
int find(int x){
for(int i=LOGA;i>=0;i--)if(x>>i){
if(lb[i]) x^=lb[i];
else return 0;
}
return 1;
}
- 是否有不同子集异或和相同/是否有非空子集异或和为 \(0\)
例题:洛谷P5556 圣剑护符
很明显这两个问题是同个问题,因为 \(x\oplus x=0\)。
同插入,如果有一个元素没有插入任何位置,说明这个元素可以被另一个子集的异或和替代,说明有不同子集异或和相同/有非空子集异或和为 \(0\)。
代码同插入。
附:最大权值无子集异或和为 \(0\) 子集
例题:BJWC2011 元素
即每个元素有值和权值,求一个子集,使得不存在这个子集的子集值异或和为 \(0\),并且这个子集权值和最大。
按权值从大到小排序,依次插入,把能插入某个线性基位置的加起来。
代码:
sort(&a[1],&a[n+1],cmp); int sm=0;
for(int i=1;i<=n;i++)if(add(x(a[i]))) sm+=y(a[i]);
printf("%d\n",sm);
- 序列子集异或成 \(x\) 的方案数/序列子集可以异或成的不同异或和数
这要用一个引理:
令 \(k=\sum_{j=0}^{{\rm max}A}[lb_j\not=0]\):
序列 \(a\{n\}\) 的子集可以异或成的不同异或和数为 \(2^k\)。
对于每个异或和 \(x\),序列 \(a\{n\}\) 有 \(2^{n-k}\) 种本质不同的子集异或和为 \(x\) 的方案。
对于 \(x=0\),\(2^{n-k}\) 种本质不同的方案中包括了空集。
怎么证明呢?考虑到每个非零线性基可以选或不选,所以异或和有 \(2^k\) 种。考虑到异或的几个灵活的性质,可以推出每个没有插入线性基的序列元素,可以选或不选,所以每个异或和 \(x\) 有 \(2^{n-k}\) 种方案。
求异或和排名同理。
代码:
//Pow
const int mod=10086;
int Pow(int a,int x){
if(a==0) return 0; int res=1;
for(;x;(a*=a)%=mod,x>>=1)if(x&1) (res*=a)%=mod;
return res;
}
scanf("%d",&q);
vector<int> in;
for(int i=0;i<=LOGA;i++)if(lb[i]) in.pb(i);
int pre=0;
for(int i=0;i<sz(in);i++)if((q>>in[i])&1) (pre+=1<<i)%=mod;
(pre*=Pow(2,n-sz(in)))%=mod;
printf("%d\n",(1+pre)%mod);
- 无向图上最大异或路径
这是线性基最玄学的操作之一。先随意生成树,对于每个环记录替换方案。具体看
吧。
代码见题解。
练习
线性基的题都是思维题。
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\)——\(\texttt{Segmenttree}\)
树链剖分,如果两点间距离 \(>30\),根据抽屉原理,输出 \(\texttt{YES}\);否则把之间的点依次插入线性基,看是否有不同子集异或和相同。代码。
用了类似图上最大异或路径的玄学操作,总体是上述多个查询的合体,具体解法略。代码。
根据 \(\texttt{SG}\) 定理,这是个最大权值无子集异或和为 \(0\) 子集模板。
其他题自己找吧,这些就是最经典巧妙的了。
祝大家学习愉快!

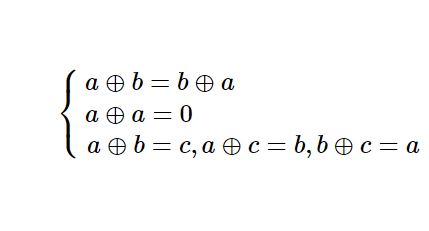 $\texttt{OI}$ 中的线性基即异或线性基,属于一种算法或数据结构。异或线性基可以解决序列子集的异或和问题,常用于出思维题。
$\texttt{OI}$ 中的线性基即异或线性基,属于一种算法或数据结构。异或线性基可以解决序列子集的异或和问题,常用于出思维题。

