题解-Magic Ship
你在 \((x_1,y_1)\),要到点 \((x_2,y_2)\)。风向周期为 \(n\),一个字符串 \(s\{n\}\) 表示风向(每轮上下左右),每轮你都会被风向吹走一格。你可以在被风吹得被动移动的基础上选择每轮移动一格或不移动。求最少几轮可以到达终点。
数据范围:\(0\le x_1,y_1,x_2,y_2\le 10^9\),\(1\le n\le 10^5\)。
一句话题解:在最优行进策略中,人离终点的距离与风周期数之间的函数单调递减;二分答案轮数。
蒟蒻的前置准备:
先通过坐标系平移简化计算:将起点 \(start\) 置为原点,则终点 \(end\) 为 \((x_2-x_1, y_2-y_1)\)。
风向字符 \(s_i\) 对应的四个字符 \('U'\),\('D'\),\('L'\),\('R'\) 分别表示上下左右走一格,对应位移向量 \(\textrm{w}\) 为:
\(\textrm{w}('U')=(0,1)\),\(\textrm{w}('D')=(0,-1)\),\(\textrm{w}('L')=(-1,0)\),\(\textrm{w}('R')=(1,0)\),字符 \(s_i\) 对应的位移向量 \(\vec{m_i}=\textrm{w}(s_i)\)。
令位移前缀和为:\(\vec{ad_i}=\sum_{j=1}^i \vec{m_i}\),则一个风周期的总位移为 \(\vec{ad_n}\)。
上式表明:尽管在一个长度为 \(n\) 轮的风周期内,人被移动的轨迹是复杂的,但每个风周期对人的轨迹影响是恒定的。因此按风周期来看,人的移动与风周期之间的关系是线性的。
设当前走了 \(k\) 轮:
假如不考虑人主动的走动,只考虑风吹人动,那么人的位置为 \(\left(ad_{k\bmod n}+ad_{n}\cdot \lfloor\frac kn\rfloor\right)\):
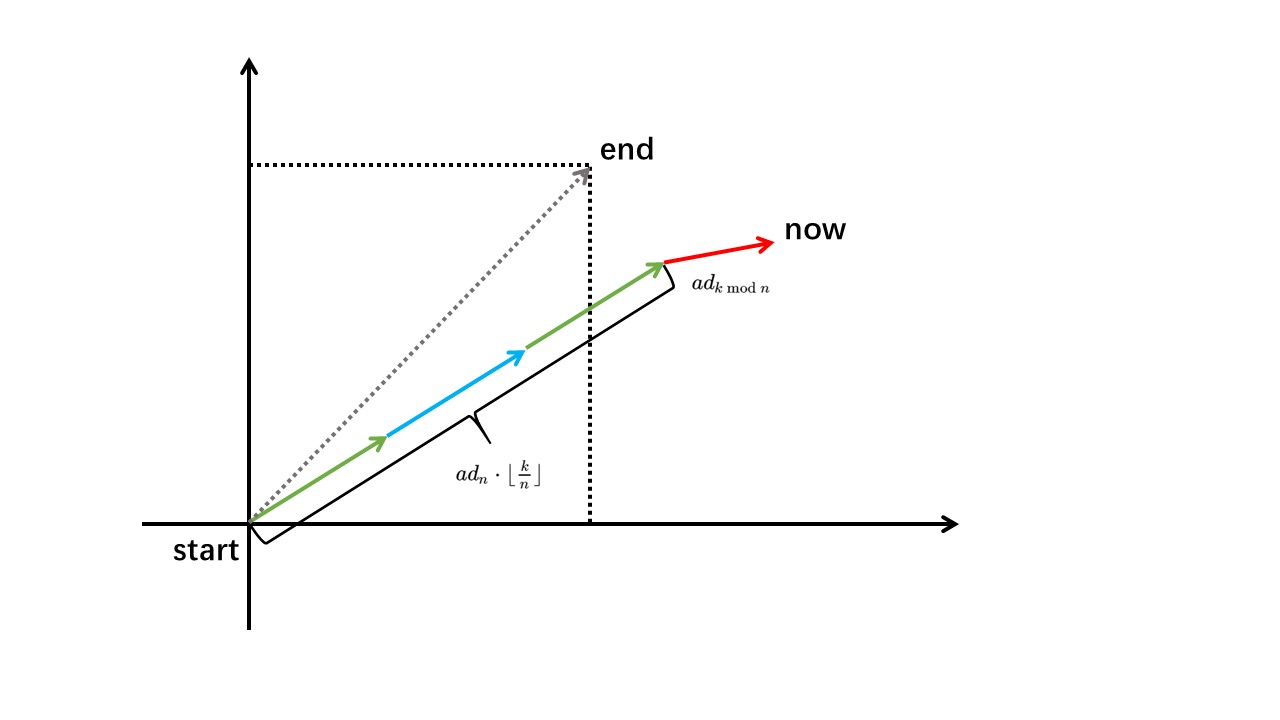
这时再考虑人的主动走动,在 \(k\) 轮中人最多走 \(k\) 步。
令 \(\textrm{dis}(a,b)\) 表示 \(a\) 和 \(b\) 两点间的曼哈顿距离(\(x\) 轴距离与 \(y\) 轴距离之和)。
所以如果 \(\textrm{dis}(end,now)\le k\),那么 \(k\) 轮以内即可到达终点。
找到单调性:
对于式子 \(\left(ad_{k\bmod n}+ad_{n}\cdot \lfloor\frac kn\rfloor\right)\):
如果枚举 \(i=k\bmod n\),则点 \(now\) 的移动轨迹可以是一条直线。
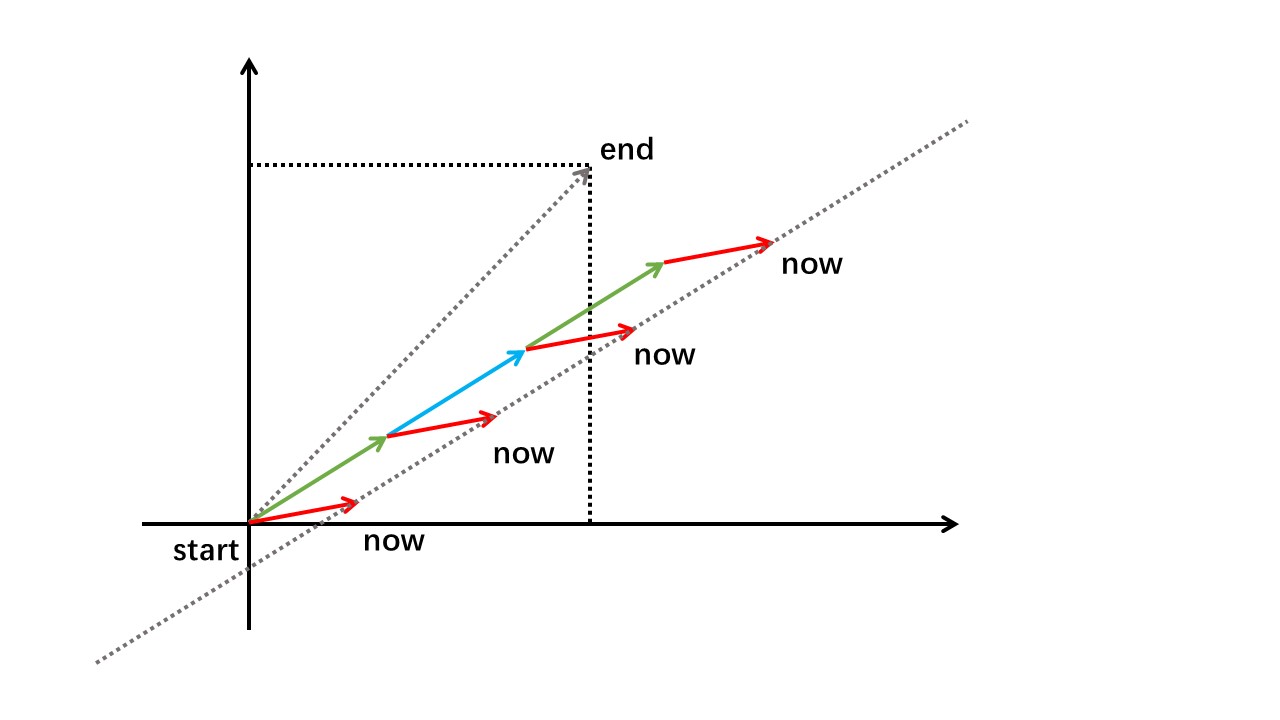
这时单独考虑 \(\textrm{dis}(end,now)\):
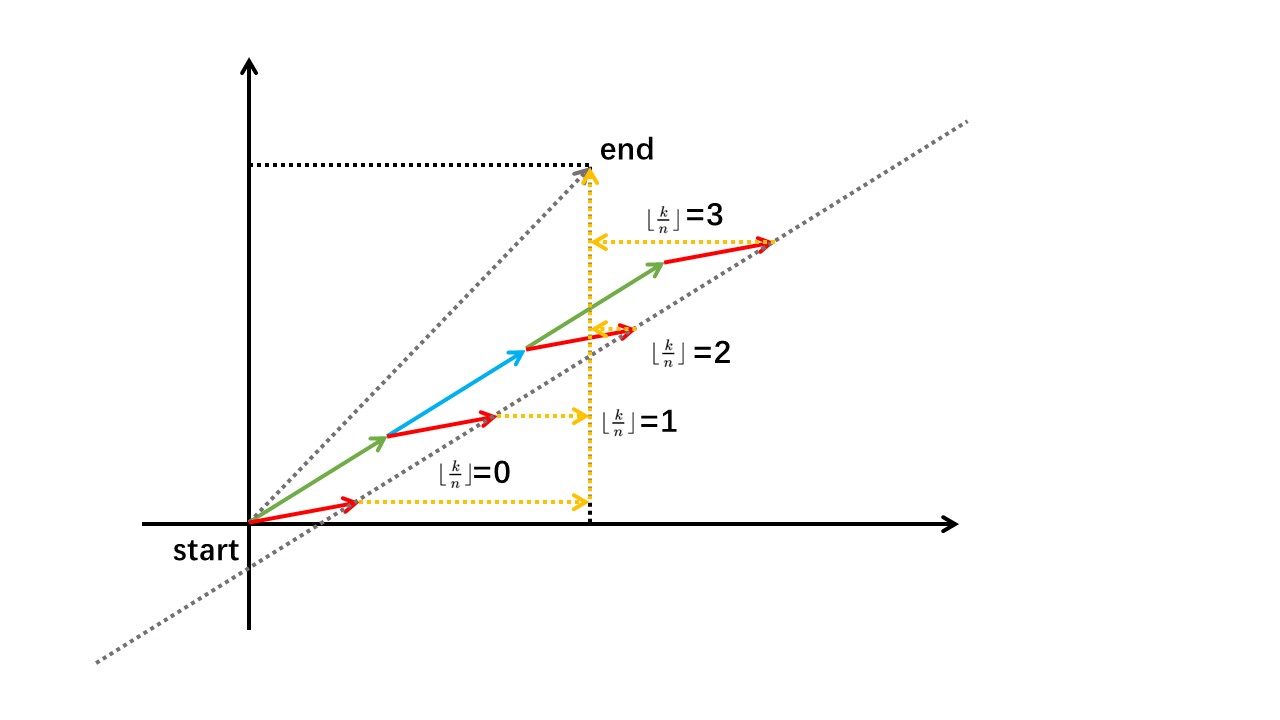
可以发现 \(\lfloor\frac kn\rfloor\leftrightarrow\textrm{dis}(end,now)\) 的函数图像如下:(如果随风就能飘到终点,折线能与 \(\lfloor\frac kn\rfloor\) 轴相切)
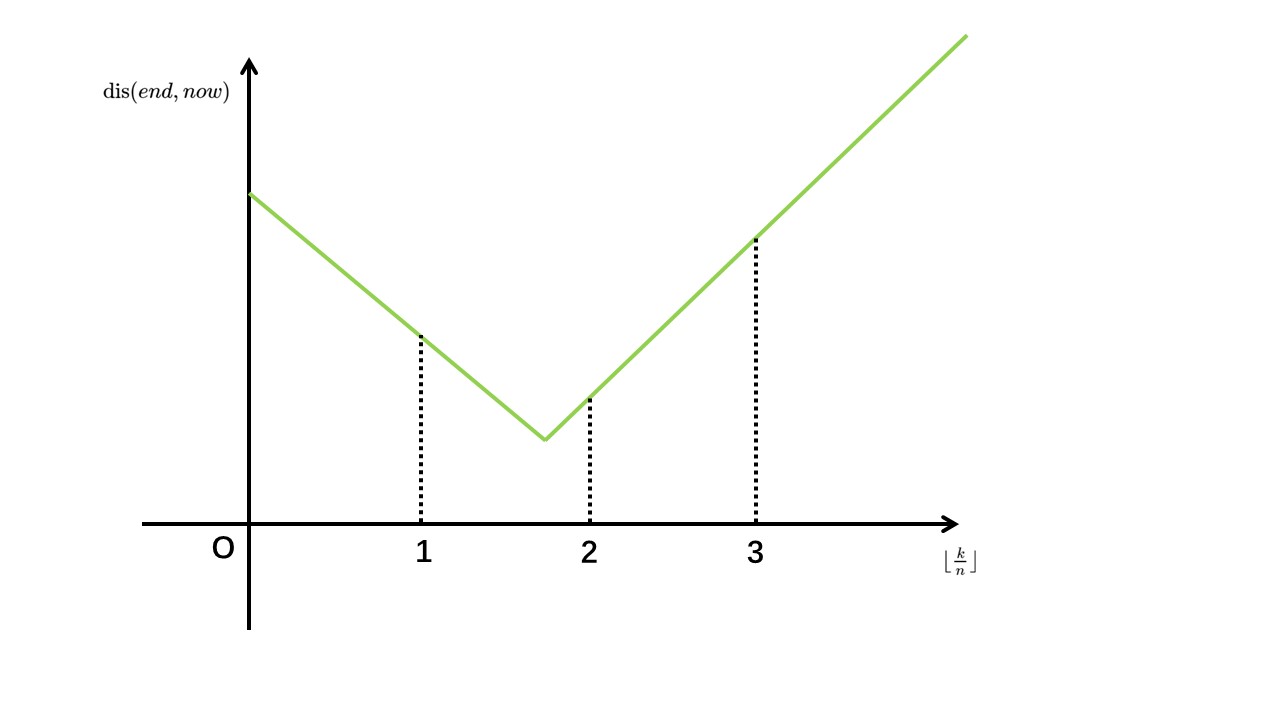
因为最终要比较 \(\textrm{dis}(end,now)\) 和 \(k\),所以作函数 \(\lfloor\frac kn\rfloor\leftrightarrow\textrm{dis}(end,now)-k\):
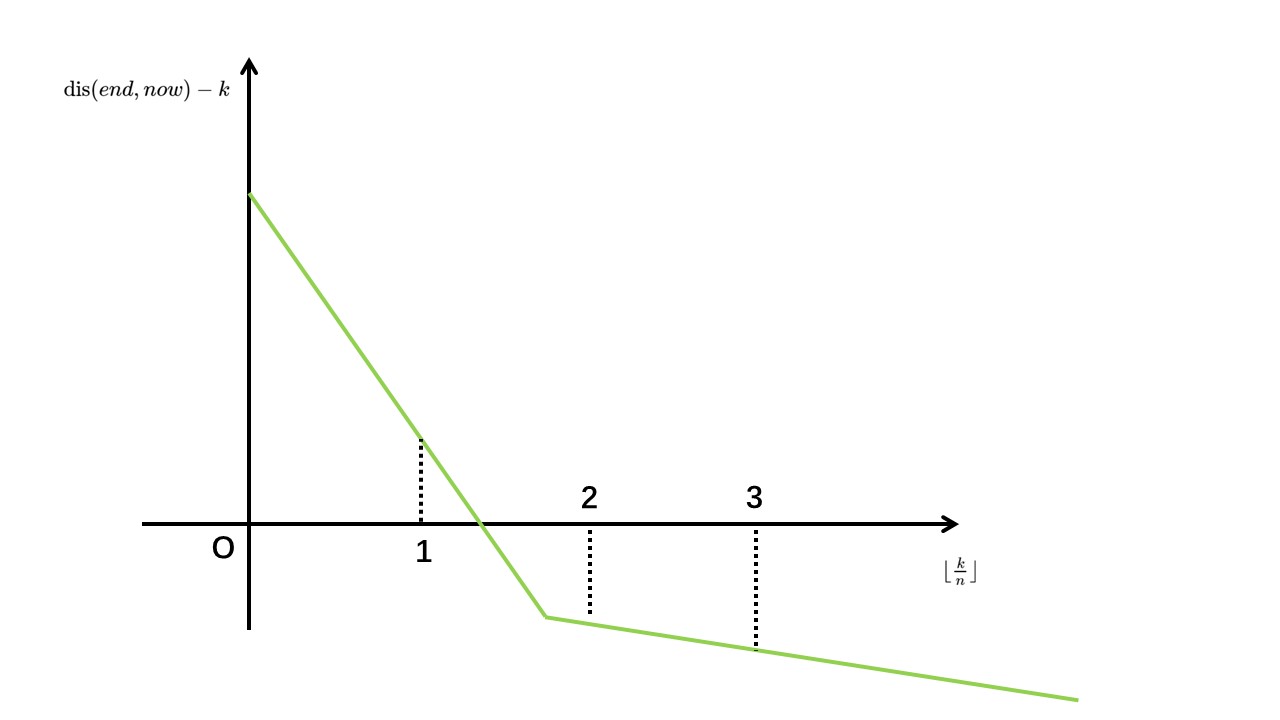
这时有个问题:这折线是否单调递减?蒟蒻拿图说服你你肯定不信,但是可以这么想:
目的是距离终点更近,风力和人力相等,所以就算风再捣乱,如果人走得和风对着干,与终点的距离也不会变大。
所以这个折线是单调递减的。
可是其实还有一种情况——该折线有平行于 \(\lfloor\frac kn\rfloor\) 轴的一段且与 \(\lfloor\frac kn\rfloor\) 轴没有交点,便说明对于当前的 \(i=k\bmod n\) 无解。
上文提到:
如果 \(\textrm{dis}(end,now)\le k\),那么 \(k\) 轮以内即可到达终点。
所以可以先如上文枚举 \(i=k\bmod n\),然后二分 \(\lfloor\frac kn\rfloor\),得到 \(\lfloor\frac kn\rfloor\leftrightarrow\textrm{dis}(end,now)-k\) 图像上 \(\le 0\) 的临界点整数 \(\lfloor\frac kn\rfloor\),\(k\) 就是对于这个 \(i\) 的答案。总答案是对于每个 \(i\) 的答案的最小值,如果对于每个 \(i\) 都无解,输出 \(-1\)。
如上图,\(\lfloor\frac kn\rfloor=2\),可以通过 \(i\) 推算出 \(k\)。
好了,小蒟蒻成功写出了一篇没人看得懂的题解。还是放代码吧(其实很短):
#include <bits/stdc++.h>
using namespace std;
//Start
#define lng long long
#define db double
#define mk make_pair
#define pb push_back
#define fi first
#define se second
#define rz resize
#define sz(x) (int)((x).size())
const int inf=0x3f3f3f3f;
const lng INF=0x3f3f3f3f3f3f3f3f;
//Data
const int N=1e5;
int n; char s[N+7];
lng ans=INF;
//Point
typedef pair<lng,lng> point;
point st,ed,ad[N+7];
lng dis(point x,point y){return abs(x.fi-y.fi)+abs(x.se-y.se);}
point operator-(const point x,const point y){return mk(x.fi-y.fi,x.se-y.se);}
point operator+(const point x,const point y){return mk(x.fi+y.fi,x.se+y.se);}
point operator*(const point x,const lng y){return mk(x.fi*y,x.se*y);}
//Main
int main(){
scanf("%lld%lld%lld%lld%d%s",&st.fi,&st.se,&ed.fi,&ed.se,&n,&s[1]);
ed=ed-st;
if(ed.fi==0&&ed.se==0) return puts("0"),0;
for(int i=1;i<=n;i++)
if(s[i]=='U') ad[i]=ad[i-1]+mk(0,1);
else if(s[i]=='D') ad[i]=ad[i-1]+mk(0,-1);
else if(s[i]=='L') ad[i]=ad[i-1]+mk(-1,0);
else if(s[i]=='R') ad[i]=ad[i-1]+mk(1,0);
for(int i=1;i<=n;i++){
lng l=-1,r=1e12+1;
while(l<r-1){
lng mid((l+r)>>1);
if(dis(ad[i]+ad[n]*(mid),ed)-mid*n-i<=0) r=mid;
else l=mid;
}
if(dis(ad[i]+ad[n]*r,ed)-r*n-i<=0) ans=min(ans,r*n+i);
}
if(ans==INF) puts("-1");
else printf("%lld\n",ans);
return 0;
}
祝大家学习愉快!


