震源机制沙滩球的绘制

震源机制解，或称断层面解，是用地球物理学方法判别断层类型和地震发震机制的一种方法。一次地震发生后，通过对不同的地震台站所接受到的地震波信号进行数学分析，即可求出其震源机制解。震源机制解不仅可以使人了解断层的类型（是正断层、逆断层还是走滑断层），而且可以揭示断层在地震前后具体的运动情况。

​ 一般震源机制解可以表示为地震断层产状（三参数：走向（strike）、倾角（dip）及滑动角（rake))与地震矩张量表示。本笔记首先给出地震断层和地震矩张量的介绍和相互关系，在给出震源机制参数的图像学表示震源沙滩球的绘制关系。

1.地震矩张量的简介

​ 若把地震的震源看作点源，矩张量（seismic moment tensor）可以用来描述地震发生时震源处发生的变形情况。通常，我们可由各台站的观测波形反演得到地震矩张量，从而确定震源机制解，进而分析地震发生时处所在构造应力场。

​ 在构造低质学中，通常可用断层的滑动，即在弹性介质内部界面的两侧不连续位移来模拟地震。然而不连续的两侧位移（即非弹性形变）就不能采用连续介质力学进行研究了。在地震学的研究中，已经证明在连续介质内部的一类体力（或组合）所产生的位移恰好与内部断层滑动所产生的位移相同。通常把这种力叫做断层模型的等效体力。有了这些体力(或组合)，就可以采用连续介质力学研究地面运动了。在描述这些等效体力和断层滑动的关系，引入地震矩张量概念描述不同等效体力组合。

​ 由于地震断层错动是由内力引起的，因此震源介质所受的净力为零（即处于平衡状态）。为了使净力为零，由于震源爆炸或断层上应力释放引起的内力，其作用的方向必须相反，大小相同。如图(1)a所示，有两个大小为\(f\)，方向相反，相隔的距离为d的力矢量的净力为零，这叫做一个力偶。这对应于爆炸（坍塌）源的一个分量。为精确描述断层错动，通常将力矢量在垂直于力的取向的方向上分开，这是就相当于两个力矢量中间有一个平行于力矢量的断层错动，这是更一般形式的力偶。为表示力偶的大小，仿照普通物理学上的力矩的概念，地震学中力的大小与这对力的作用点分开的距离的乘积表示该力偶的大小，表示震源向外拉张的大小，则表示使震源介质旋转的力矩大小。这样一个力偶的作用会导致有一个围绕力偶中心点的力矩，该力矩会使得震源介质顺时针旋转起来，除非还存在一对互补的力偶来平衡该力矩，再增加一个力矢量方向垂直于前述力矢量方向的力偶使得震源介质具有逆时针方向旋转的力矩，这使得震源介质的净力矩为零（角动量守恒）。这种力偶，叫做双力偶。

​ 为了描述不同位态的力偶，在笛卡尔坐标系里定义力偶\(M_{ij}\) 为一对作用在\(i\)方向上的力偶与\(j\) 方向的力偶，其中沿\(i\)方向的力位于\(j\)的增加方向，而沿逆\(i\)方向的力位于\(j\)减少方向，图2展示了9种不同的力偶。\(M_{ij}\) 的大小乘积\(fd\) ,在点源极限的情况下\(d\rightarrow 0\) 时，\(M_{ij}\) 为常数，因而自然地定义了矩张量\(M\)​ :

​ 角动量守恒的条件要求\(M\) 是对称的，即\(M_{ij}=M_{ji}\) 。因此，地震矩张量 \(M\) 只有6个独立元素。地震矩张量描述了在弹性介质内产生的可能作用在某一点的体力通常表示。虽然这是理想化的，但可以证明，这是模拟地震震源的尺度远小于观测到的地震波长的，远离震源的台站上的地震响应的最好的近似表达。大尺度的，更加复杂的震源（如汶川地震）也可以通过对不同位置的点力求和来模拟。

​ 请大家注意，上面描述的各种位态的力偶不能理解为一个震源错动中有多种位态力偶所表示的错动，而是它们组合为两个在空间任意形态的，大小不同的力偶的错动，这类似于一个力可以分解为不同坐标分量，不能理解为几个不同的力一样。如何组合不同大小的各种位态的力偶表示一个地震破裂。

1.1 地震矩张量的物理意义

​ 在上面引入地震矩张量的概念，并给出其与辐射地震波的关系，本小节讨论其物理意义。

A1 断层及膨胀(坍缩)源的地震矩张量表示

​ 根据图2，走向为\(x\)​方向的垂直断层的右旋运动可以用的矩张量表示：

\[\boldsymbol{M}=\left[\begin{array}{ccc} 0 & M_0 & 0 \\ M_0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right] \tag{1} \]

式中，\(M_{0}\)​​叫做标量地震矩，为：

\[M_{0}=\mu DA \tag{2} \]

\(M_{0}\)的单位是\(Nm\),与前面定义的力偶的单位相同。根据不同力偶的取向，容易看出怎么样矩张量来描述任意走向、倾角、滑动角的断层。然而，一般来说，可以通过矩张量作适当的旋转来描述断层和任意取向的滑动。

​ 因为\(M_{ij}=M_{ji}\)，所以相应的双力偶模型有两种可能的断层面。例如，式(1)对于走向沿\(y\)轴的左旋断层也是合适的。两个可能的断层面有相同的矩张量描述。在用地震观测来反演断层模型时，需要特别注意。对双力偶模型，一般来说，两个可能的断层面都与远距离的地震观测结果相吻合。实际的断层面叫做主断层面，另一个断层面叫做辅助断层面。这种模糊不是双力偶模型的欠缺（可以证明它与地震观测结果吻合得最好），而是反映两个断层在远场产生相同位移的基本事实。要对主断层面和辅助断层面做出基本识别，需要根据其他研究或者使用其他资料（例如，余震的位置或观测到的地表破裂）。

​ 因为矩张量是对称的，可以通过计算它的特征向量与特征值及将其旋转到新的坐标系里，把矩张量对角线化。下图给出矩张量的坐标旋转的例子。主轴相对于原坐标\(x\)轴和\(y\)​轴的角度为45度，旋转后地震矩张量变为

\[\boldsymbol{M}^{\prime}=\left[\begin{array}{ccc} M_0 & 0 & 0 \\ 0 & -M_0 & 0 \\ 0 & 0 & 0 \end{array}\right] \tag{3} \]

根据前面矩张量元素的定义可知，坐标\(x^{'}\)方向为拉开轴\(T\),\(y^{'}\)为压缩力偶的方向定义为\(P\)。采用MATLAB求解坐标的变换的语句为：

M=[0 1 0;1 0 0;0 0 0];
[V,D]=eig(M);
可得

V=[-0.7071 0 0.7071; 0.7071 0 0.7071;0 1.0000 0];

M=[-1 0 0;0 0 0;0 0 1];

可知，地震矩的特征值为-1，对应的特征向量\([-0.7071,0.7071,0]^{T}\); 特征值为1，对应的特征向量为\([0.7071,0.7071,0]^{T}\), 与\(x\)轴和\(y\)轴分别夹角\(45^{0}\),则得该旋转的矩张量为\([1, 0 ,0;0 ,-1 ,0;0, 0,0]\); 在新坐标系中的矩张量表示为式（3)。这相当于\(y^{'}\)轴上的挤压力和\(x^{'}\) 轴的拉张力导致了这种双力偶震源错动。因此，\(y^{'}\)轴为压缩轴，简称为P轴。\(x^{'}\)轴为拉张轴，简称为T轴。而与\(x^{'}\)和\(y^{'}\) 垂直的轴为中间轴，简称B轴或N轴，这三个轴是正交的。

​ 对于一般的地震矩张量，中间特征值不一定为零。三个特征值之和（即地震矩张量的迹）为地震矩张量的第一不变量（转换到其他坐标系下的对角线元素之和不变）。对于地震矩张量，矩张量的迹则表示膨胀源（或坍缩源）分量。如果膨胀或者坍缩源为各向同性的，则矩张量有简单的形式：

\[\boldsymbol{M}=\left[\begin{array}{ccc} M_{x x} & 0 & 0 \\ 0 & M_{y y} & 0 \\ 0 & 0 & M_{x z} \end{array}\right] \tag{4} \]

式中，\(M_{xx}=M_{yy}=M_{zz}=1/3trace(M)\) 。反之，迹为零的地震矩张量，体积变化为0，表示剪切破裂或双力偶震源破裂分量。

A2 一般矩张量的分解

​ 一般地震矩张量可以分解为各向同性（isotropy）和偏量（deviatoric）部分，在主轴坐标系下可以表示为：

\[\boldsymbol{M}=\left[\begin{array}{ccc} M_1 & 0 & 0 \\ 0 & M_2 & 0 \\ 0 & 0 & M_3 \end{array}\right]=\frac{1}{3}\left[\begin{array}{ccc} \operatorname{tr}(\boldsymbol{M}) & 0 & 0 \\ 0 & \operatorname{tr}(\boldsymbol{M}) & 0 \\ 0 & 0 & \operatorname{tr}(\boldsymbol{M}) \end{array}\right]+\left[\begin{array}{ccc} M_1^1 & 0 & 0 \\ 0 & M_2^1 & 0 \\ 0 & 0 & M_3^1 \end{array}\right] \tag{5} \]

式中，\(tr(M)=M_{1}+M_{2}+M_{3}\), 是矩阵\(M\)的迹。余项\(M_{i}^{1}\)为\(M\) 的纯偏特征值。由迹给出的各向同性对应于由爆炸或坍缩破裂引起的部分。大部分震源具有很小的各向同性成分，确定断层事件的地震矩张量时，通常添加\(tr(M)=0\)的约束。

​ 矩张量的另一种分解是将矩张量分解为一个各向同性分量和三个双力偶分量，假定地震矩张量的三个特征值\(M_{1} \geq M_{2} \geq M_{3}\) ,则

\[\begin{aligned} & \boldsymbol{M}=\left[\begin{array}{ccc} M_1 & 0 & 0 \\ 0 & M_2 & 0 \\ 0 & 0 & M_3 \end{array}\right]=\frac{1}{3}\left[\begin{array}{ccc} \operatorname{tr}(\boldsymbol{M}) & 0 & 0 \\ 0 & \operatorname{tr}(\boldsymbol{M}) & 0 \\ 0 & 0 & \operatorname{tr}(\boldsymbol{M}) \end{array}\right]+\frac{1}{3}\left[\begin{array}{ccc} M_1-M_2 & 0 & 0 \\ 0 & -\left(M_1-M_2\right) & 0 \\ 0 & 0 & 0 \end{array}\right] \\ & +\frac{1}{3}\left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & M_2-M_3 & 0 \\ 0 & 0 & -\left(M_2-M_3\right) \end{array}\right]+\frac{1}{3}\left[\begin{array}{ccc} M_1-M_3 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -\left(M_1-M_3\right) \end{array}\right] \\ & \end{aligned} \tag{6} \]

式(6)中每一个偏项都是一个双力偶。

​ 矩张量的其他分解包含补偿线性向量偶极( compensated linear vector dipole, CLVD)。这种补偿线性向量偶极在一个特征值方向有一个两倍强度的偶极，而在另外两个特征值方向上是单位强度的偶极。一般矩张量还可以分解为各向同性部分和三个主轴方向上的补偿线性向量偶极。

\[\begin{aligned} \boldsymbol{M}= & {\left[\begin{array}{ccc} M_1 & 0 & 0 \\ 0 & M_2 & 0 \\ 0 & 0 & M_3 \end{array}\right]=\frac{1}{3}\left[\begin{array}{ccc} \operatorname{tr}(\boldsymbol{M}) & 0 & 0 \\ 0 & \operatorname{tr}(\boldsymbol{M}) & 0 \\ 0 & 0 & \operatorname{tr}(\boldsymbol{M}) \end{array}\right]+\frac{1}{3}\left[\begin{array}{ccc} 2 M_1 & 0 & 0 \\ 0 & -M_1 & 0 \\ 0 & 0 & -M_1 \end{array}\right] } \\ & +\frac{1}{3}\left[\begin{array}{ccc} -M_2 & 0 & 0 \\ 0 & 2 M_2 & 0 \\ 0 & 0 & -M_2 \end{array}\right]+\frac{1}{3}\left[\begin{array}{ccc} -M_3 & 0 & 0 \\ 0 & -M_3 & 0 \\ 0 & 0 & 2 M_3 \end{array}\right] \end{aligned} \tag{7} \]

​ 另一种通常的分解是将矩张量分解为一个大力偶和一个小力偶。大双力偶是地震矩张量具有相同主轴的双力偶表示的最好近似。因此大力双偶也称为“最佳双力偶模型”。由于矩张量的纯偏量部分的迹\(M_{1}^{1}+M_{2}^{1}+M_{3}^{1}=0\)，其中当矩张量的偏量部分的特征值为\(M_{1}^{1},M_{2}^{1},M_{3}^{1}\)，当\(\left|M_1^1\right| \geqslant\left|M_2^1\right| \geqslant\left|M_3^1\right|\) 时，有

\[\boldsymbol{M}=\left[\begin{array}{ccc} M_1 & 0 & 0 \\ 0 & M_2 & 0 \\ 0 & 0 & M_3 \end{array}\right]=\frac{1}{3}\left[\begin{array}{ccc} \operatorname{tr}(\boldsymbol{M}) & 0 & 0 \\ 0 & \operatorname{tr}(\boldsymbol{M}) & 0 \\ 0 & 0 & \operatorname{tr}(\boldsymbol{M}) \end{array}\right]+\left[\begin{array}{ccc} M_1^1 & 0 & 0 \\ 0 & -M_1^1 & 0 \\ 0 & 0 & 0 \end{array}\right]+\left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & -M_3^1 & 0 \\ 0 & 0 & M_3^1 \end{array}\right] \tag{8} \]

式中，\(M_{2}^1=-M_{1}^1-M_{3}^1\)。第二项为大双力偶（最佳双力偶），含有最大特征值，而另一个双力偶为小双力偶。如果\(M_{3}^1=0\),则最小双力偶为零，地震矩张量完全分解为地震矩张量各向同性部分和一个双力偶部分。

​ 还有一种研究将地震矩张量分解为一个各向同性，一个双力偶和一个补偿线性向量偶极。同样对于\(\left|M_1^1\right| \geqslant\left|M_3^1\right|\) ,则\(M_{1}^1\)和\(M_{2}^1\)与\(M_{3}^1\)的符号必定相反。定义\(F=-\frac{M_2^1}{M_1^1}\),则有\(0\leq F\leq 1/2\)。从而有\(M_{2}^1=-FM_{1}^1,M_{3}^1=(F-1)M_{1}^1\)。地震矩张量的偏量部分可以表示为：

\[\begin{aligned} & M^{'}=\left[\begin{array}{ccc} M_1^1 & 0 & 0 \\ 0 & M_2^1 & 0 \\ 0 & 0 & M_3^1 \end{array}\right]=M_1^1\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & -F & 0 \\ 0 & 0 & F-1 \end{array}\right]=M_1^1\left[\begin{array}{ccc} 1-2 F+2 F & 0 & 0 \\ 0 & -F & 0 \\ 0 & 0 & 2 F-1-F \end{array}\right] \\ & =M_1^1(1-2 F)\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{array}\right]+M_1^1 F\left[\begin{array}{ccc} 2 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{array}\right] \\ & \end{aligned} \tag{9} \]

由式(9)可见，因子\(F\)表示了 补偿线性向量偶极与纯双力偶源的比例，当\(F=0\)，偏量部分仅含双力偶，此时\(M_{2}^1=0,M_{3}^1=-M_{1}^1\);当\(F=-1/2\)时，偏量部分仅含补偿线性向量偶极，此时\(M_{2}^1=M_{3}^1=-M_{i}^1/2\)。由于\(0\leq F\leq1/2\)，所以习惯上常用\(200F\%\)来表示补偿线性向量偶极的相对强度，用\(100(1-2F)\%\)来表示纯双力偶的相对强度，两者之和为\(100\%\)。在研究火山区或坍塌地区的地震矩张量时，通常采用这种表示。

2.地震断层与地震矩张量

​ 在上一节中介绍各种位态的力偶，并说明可以用它们的组合来表示地震破裂。本节讨论地质上描述的断层错动与地震矩张量的关系，地震矩张量除了能表示地震错动外，还能表示震源的何种特性。本节首先介绍地质上的断层错动描述，然后讨论地震矩张量的意义，最后给出断层错动转换为地震矩张量描述的方法。

2.1地震断层参数

​ 地质上通常理想化地把地震看成是任意取向的平面断层两侧的运动。断层面由它的走向（strike \(\phi\), 即断层与水平地表交线相对于北的角度），倾角（dip \(\delta\) ,相对于水平面的角度）规定。对于非垂直的断层，断层面之上的叫做上盘（up wall），之下的叫做下盘（foot wall）。这里需要注意，地质定义的断层走向可以沿断层迹线向两个方向延伸，而在地震学中定义的断层走向为观测者站在断层上盘看断层迹线，右侧为其走向，左侧不是其走向。滑动矢量按上盘相对于下盘的运动来定义。滑动角\(\lambda\) （rake angle）是滑动矢量和走向之间的夹角。上盘向上运动的断层叫做正断层（normal fault），反之，上盘向下运动的叫做逆断层（thrust fault）。倾角小于45度的逆断层叫做冲断层，近于水平的冲断层叫做逆掩断层。一般来说，逆断层包含有垂直于走向上的水平压缩，而正断层则有水平拉涨。断层面之间的水平运动叫做走滑（strike slip），垂直运动叫做倾滑（dip slip）。如果站在断层一边的观测者看到邻近的体块向右运动，叫做右旋走滑断层（反之，为左旋走滑断层）。滑动角\(\lambda\) 是断层走向逆时针旋转至滑动矢量方向所用的夹角，对于逆冲断层，\(\lambda=90\), 对于正断层而言，\(\lambda=-90或者270\) ，左旋断层\(\lambda=0\), 右旋断层\(\lambda=180\)​。

图1 震源球和其对应断层几何形状

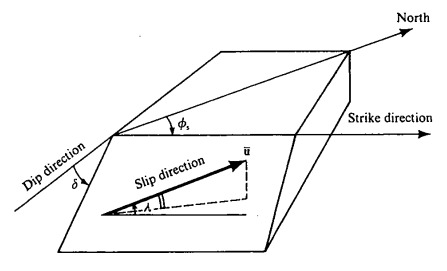
​ 在地震学中，走向(\(0\leq\phi<360\)), 倾角（\(0\leq\delta\leq90\)），滑动角（\(0\leq\lambda\leq360或者-180\leq\lambda\leq180\)）和滑动矢量的值\(D\)规定了断层的最基本的地震模型或地震的震源机制。

2.2 断层面参数与地震矩张量的转换公式

​ 在上一节给出了地震断层描述和地震矩张量描述的关系，在本节将描述断层滑动的具体参数与地震矩张量的表达式。在地震学问题的表述中，通常采用北东下坐标系。在断层描述中，假定断层的走向为\(\phi\) ,倾角为\(\delta\) ,滑动角为\(\lambda\) ,则在北东下坐标系通过三次坐标转换来得到以断层走向，倾向和法向为坐标轴的坐标系。

​ 断层面的滑动方向为\(X_{3}\)方向，斜向下的方向为\(Y_{3}\), 与断层面垂直的方向为\(Z_{3}\)，将其表示在地平坐标系\(XYZ\)中(\(X\)对应于北向，\(Y\)轴对应于东向，\(Z\)轴对应于下轴)。地平坐标旋转为应力主轴坐标系中。

（1）\(XYZ\)坐标系沿\(Z\)轴正向看去，绕\(Z\)轴顺时针转动\(\phi\)角得到\(X_{1}Y_{1}Z_{1}\)。旋转公式为：

\[\left[\begin{array}{l} X_1 \\ Y_1 \\ Z_1 \end{array}\right]=\left[\begin{array}{ccc} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} X \\ Y \\ Z \end{array}\right]\tag{10} \]

（2）\(X_{1}Y_{1}Z_{1}\) 沿\(X_{1}\) 轴正向看去，绕\(X_{1}\) 轴顺时针转动\(\delta\) 角得到\(X_{2}Y_{2}Z_{2}\) ,旋转公式为：

\[\left[\begin{array}{l} X_2 \\ Y_2 \\ Z_2 \end{array}\right]=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \delta & \sin \delta \\ 0 & -\sin \delta & \cos \delta \end{array}\right]\left[\begin{array}{l} X_1 \\ Y_1 \\ Z_1 \end{array}\right]=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \delta & \sin \delta \\ 0 & -\sin \delta & \cos \delta \end{array}\right]\left[\begin{array}{ccc} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} X \\ Y \\ Z \end{array}\right] \tag{11} \]

（3） \(X_{2}Y_{2}Z_{2}\) 沿\(Z_{2}\) 轴正向看去，绕\(Z_{2}\)轴逆时针转动得到\(X_3Y_3Z_3\) ,旋转公式得到

\[\begin{aligned} {\left[\begin{array}{l} X_3 \\ Y_3 \\ Z_3 \end{array}\right]=} & {\left[\begin{array}{ccc} \cos \lambda & -\sin \lambda & 0 \\ \sin \lambda & \cos \lambda & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} X_2 \\ Y_2 \\ Z_2 \end{array}\right] } \\ & =\left[\begin{array}{ccc} \cos \lambda & -\sin \lambda & 0 \\ \sin \lambda & \cos \lambda & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \delta & \sin \delta \\ 0 & -\sin \delta & \cos \delta \end{array}\right]\left[\begin{array}{ccc} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} X \\ Y \\ Z \end{array}\right] \\ & =\left[\begin{array}{ccc} \cos \phi \cos \lambda+\sin \varphi \cos \delta \sin \lambda & \sin \phi \cos \lambda-\cos \phi \cos \delta \sin \lambda & -\sin \delta \sin \lambda \\ \cos \phi \sin \lambda-\sin \phi \cos \delta \cos \lambda & \sin \phi \sin \lambda+\cos \phi \cos \delta \cos \lambda & \sin \delta \sin \lambda \\ \sin \phi \sin \delta & -\cos \phi \sin \delta & \cos \delta \end{array}\right]\left[\begin{array}{l} X \\ Y \\ Z \end{array}\right] \end{aligned} \tag{12} \]

通过上面的转换后，\(X_{3}\) 轴就对应于断层的滑动方向，\(Z_{3}\) 轴垂直于断层面指向斜下放。指向斜上方的矢量将\(Z_3\)​的方向指向加一符号即可。

​ 假定断层错动量为\(\bar{D}\) ,则断层错动的滑动矢量采用断层参数的表示形式为：

\[\boldsymbol{D}=\bar{D}(\cos \phi \cos \lambda+\sin \phi \cos \delta \sin \lambda) \boldsymbol{i}+\bar{D}(\sin \phi \cos \lambda-\cos \phi \cos \delta \sin \lambda) \boldsymbol{j}-\bar{D} \sin \delta \sin \lambda \boldsymbol{k} \tag{13} \]

​ 断层法向采用\(Z_{3}\) 反方向为：

\[\boldsymbol{n}=-\sin \phi \sin \delta \boldsymbol{i}+\cos \phi \sin \delta \boldsymbol{j}-\cos \delta \boldsymbol{k} \tag{14} \]

任意取向的双力偶作用在一具有滑动矢量\(\boldsymbol{D}\) 和法向量\(\boldsymbol{n}\) 的断层面上。在上面的笔记中，根据地震矩的定义及物理意义，但在那里对应于一个方向的错动产生的地震矩。知道绕\(Z\)轴的力矩由沿X方向的与\(Y\)方向作用点错开的力臂的乘积与沿\(Y\)方向的力和\(x\)方向上作用点错开力臂的乘积之和。假定\(x\)方向上作用点错开的力臂为\(L_{x}\) ,在力臂前方作用点的\(y\)方向的位移为\(D_{x}\),\(y\)方向上作用点错开力臂为\(L_{y}\) ,在力臂前方作用点。\(x\)方向的力使\(y\)轴旋转\(D_{x}/L_{y}\) 的角度；\(y\)方向的力使\(x\)轴旋转\(D_{y}/L_{x}\) 的角度。这个旋转角度与剪切模量\(\mu\) 的乘积即为剪切应力，剪切应力与作用面积\(A\)的乘积即为剪切力的大小。将沿\(x\)方向和\(y\)方向的剪切力与各自作用力臂的乘积之和 , 即

\[{M_{xy}} = \left( {\mu \frac{{{D_x}}}{{{L_y}}}} \right)A{L_y} + \left( {\mu \frac{{{D_y}}}{{{L_x}}}} \right)A{L_x} = \mu A\left( {{D_k}{n_j} + {D_j}{n_k}} \right) \tag{15} \]

以此类推，对于地理坐标系或任意其他坐标系，断层面积为\(A\)的矩张量\(M_{kj}=\mu A(D_{k}n_{j}+D_{j}n_{k})\) ，可以得到

\[\begin{aligned} & M_{x x}=-M_0\left(\sin \delta \cos \lambda \sin 2 \phi+\sin 2 \delta \sin \lambda \sin ^2 \phi\right) \\ & M_{y y}=M_0\left(\sin \delta \cos \lambda \sin 2 \phi-\sin 2 \delta \sin \lambda \cos ^2 \phi\right) \\ & M_{x z}=M_0(\sin 2 \delta \sin \lambda)=-\left(M_{x x}+M_{y y}\right) \\ & M_{x y}=M_0\left(\sin \delta \cos \lambda \cos 2 \phi+\frac{1}{2} \sin 2 \delta \sin \lambda \sin 2 \phi\right) \\ & M_{x z}=-M_0(\cos \delta \cos \lambda \cos \phi+\cos 2 \delta \sin \lambda \sin \phi) \\ & M_{y z}=-M_0(\cos \delta \cos \lambda \sin \phi-\cos 2 \delta \sin \lambda \cos \phi) \end{aligned} \tag{16} \]

此处\(M_{0}\)​​ 为标量地震矩。式（16）结果表明：（1）滑动矢量和断层面法向矢量的可交换性使得地震矩张量为对称张量，这个在物理上对应于断层面和辅助面的错动产生的辐射花样是一样的；（2）采用断层面参数计算的地震矩张量的迹为零。这个容易理解，断层面错动为剪切位错源，没有膨胀或坍塌的成分，而矩张量的迹对应于膨胀或坍塌的成分；

下面给出GMT中北东下坐标系中矩张量的转换的MATLAB程序如下：

function [mt]=sdr2mt(strike,dip,rake)
%SDR2MT    Convert strike-dip-rake to moment tensor
%
%    Usage:    mt=sdr2mt(sdr)
%              mt=sdr2mt(strike,dip,rake)
%
%    Description:
%     MT=SDR2MT(SDR) converts a double-couple (aka focal mechanism) given
%     in strike-dip-rake form (Nx3) as [strike dip rake] to Harvard moment
%     tensor form (Nx6) as [Mrr Mtt Mpp Mrt Mrp Mtp] which uses the Up,
%     South, East coordinate system.  N allows for multiple focal
%     mechanisms to be converted simultaneously.  The main purpose of this
%     function is to allow plotting of the focal mechanism with PLOTMT.
%     Strike is positive clockwise from North, dip is positive downward
%     from the horizontal and rake is positive counter-clockwise in the
%     fault plane from the strike direction.  Note that the strike must be
%     such that when you look along the direction of the strike the fault
%     dips to your right.
%
%     MT=SDR2MT(STRIKE,DIP,RAKE) allows inputing the strike, dip & rake
%     separately.  Note that the inputs should all be Nx1 column vectors or
%     scalars.
%
%    Notes:
%     - Tested OK against George Helffrich's website:
%        http://www1.gly.bris.ac.uk/~george/focmec.html
%     - See Aki & Richards (2002) Figure 4.20 & Box 4.4 for details.
%
%    Examples:
%     % Plot a dip-slip fault with EW strike and 45 deg dip:
%     plotmt(0,0,sdr2mt(90,45,-90))
%     axis tight equal off
%
%     % Validate SDR2MT & MT2SDR using GlobalCMT catalog:
%     cmts=findcmts;
%     sdr1=[cmts.strike1 cmts.dip1 cmts.rake1];
%     sdr2=[cmts.strike2 cmts.dip2 cmts.rake2];
%     sdr3=mt2sdr(sdr2mt(sdr1));
%     max(min(abs(azdiff(sdr3,sdr1)),abs(azdiff(sdr3,sdr2))))
%     sdr4=mt2sdr(sdr2mt(sdr2));
%     max(min(abs(azdiff(sdr4,sdr1)),abs(azdiff(sdr4,sdr2))))
%
%    See also: MT2SDR, AUXPLANE, PLOTMT, MT_DECOMP, MT_DIAG, MT_UNDIAG

%     Version History:
%        Mar.  8, 2010 - initial version
%        June  1, 2011 - harvard output, now with docs
%        Mar. 21, 2013 - doc update, clean up code, no mt cmp output
%        Mar. 25, 2013 - minor doc update
%
%     Written by Garrett Euler (ggeuler at wustl dot edu)
%     Last Updated Mar. 25, 2013 at 13:50 GMT

% todo:

% check nargin

% convert strike-dip-rake to HRV mt
% f = strike, d = dip, l = rake
%1 Mrr =  Mzz =  Mo sin2d sinl
%2 Mtt =  Mxx = -Mo(sind cosl sin2f +     sin2d sinl (sinf)^2 )
%3 Mpp =  Myy =  Mo(sind cosl sin2f -     sin2d sinl (cosf)^2 )
%4 Mrt =  Mxz = -Mo(cosd cosl cosf  +     cos2d sinl sinf )
%5 Mrp = -Myz =  Mo(cosd cosl sinf  -     cos2d sinl cosf )
%6 Mtp = -Mxy = -Mo(sind cosl cos2f + 0.5 sin2d sinl sin2f )

mt=nan(numel(strike),6);
mt(:,1)=sind(2*dip).*sind(rake);
mt(:,2)=sind(dip).*cosd(rake).*sind(2*strike) ...
    + sind(2*dip).*sind(rake).*sind(strike).^2;
mt(:,3)=sind(dip).*cosd(rake).*sind(2*strike) ...
    - sind(2*dip).*sind(rake).*cosd(strike).^2;
mt(:,4)=cosd(dip).*cosd(rake).*cosd(strike) ...
    + cosd(2*dip).*sind(rake).*sind(strike);
mt(:,5)=cosd(dip).*cosd(rake).*sind(strike) ...
    - cosd(2*dip).*sind(rake).*cosd(strike);
mt(:,6)=sind(dip).*cosd(rake).*cosd(2*strike) ...
    + 0.5.*sind(2*dip).*sind(rake).*sind(2*strike);
mt(:,2:2:6)=-mt(:,2:2:6);

end

​ 当前，有些地震学家采用不同的坐标系来定义地震矩张量。如下，在自由震荡分析中采用\(r\),\(\theta\),\(\phi\) 分别表示上南动方向，并组成坐标系。在这种坐标系下矩张量与北东下坐标系的变换关系为：

\[M_{rr}=M_{zz},M_{\theta\theta}=M_{xx},M_{r\theta}=M_{xz},M_{r\phi}=-M_{yz},M_{\theta\phi}=-M_{xy} \tag{17} \]

在该坐标系用于全球常规的矩心矩张量反演中。

2.3 震源机制参数的相互转换

​ 根据第1节的内容，根据远震地震波记录，能够得到地震的两个可能的断层面。每个可能断层的运动可以用走向（strike）、倾角(dip)、和滑动角(rake)来描述，另外，描述地震震源还可以用压缩轴（P轴）、中间轴（B轴）和压缩轴（T轴）来描述的走向（trend）和倾伏角（plunge）来描述。但除了地震矩大小外，这些参数只有三个是独立的，其它参数可以通过给定的三个独立参数给出。本节笔记讨论地震震源机制参数的相互转换。

3.震源机制参数的图形表达—震源球（沙滩球）

​ 地震的基本破裂模式可用断层的参数的走向（strike）、倾角（dip）和滑动角（rake）来描述，这就是地震的剪切位错源表达的震源机制。对于剪切位错源，震源球的两个节面（其中之一为可能的断层面）将P波辐射图像分为四个卦象。就表示了地震的基本破裂模型，但如果每个震源机制都在地图上画出三维辐射样式图，是非常不方便的。

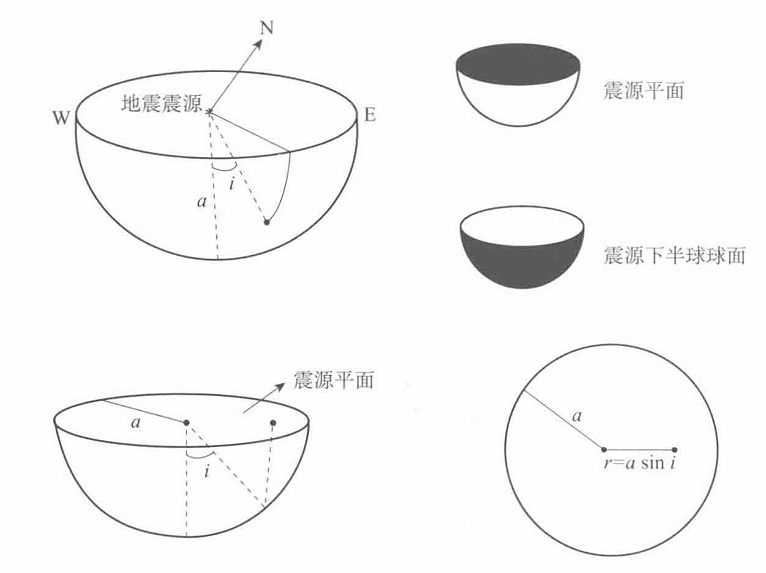
​ 为了将破裂模式表示在地图上，通常将震源球投影到水平面切割震源球的大圆上，将震源球面上的正负象限采用不同的颜色（阴影）表示在大圆内。这样就有两种选择，可以将水平面以上半球投影到水平面，也可以将水平面以下的投影到水平面内。在地震学研究中，大多数地震射线向下弯曲到达地震台站（特别是远震），因此，如不特别说明，则震源球采用下半球投影。如图，直接从正上方看下班球的点，点到圆心的距离的\(r\)应满足：

\[r = a\sin i \]

虽然这种投影符合我们在地图上的观测，但在下半球上的两条互相垂直的弧投影到水平面的圆内通常就不垂直了，并且在下半球上的均匀分布的点投影到圆内，边缘投影点密集而中心稀疏。为了改善这种情况，通常采用两种投影：（1）\(Wulff\) 投影；（2）等面积投影； 下面分别介绍这两种投影方法。

图2 震源球的投影表示

3.1 Wulff投影表示

​ 与上面一样，投影平面为震源球面过球心的水平大圆面(称为赤平面)。投影点为大圆面相对的极点\(N\)。如下图所示，若某射线透过下半球面的\(A\)点到达台站，则其在投影图上的投影点为\(A^{'}\)。如果某射线从震源向上发出，穿过震源球面上的\(R\)点到达台站，可将射线\(RO\)经过震源\(O\)向反方向延伸至震源球面上的对折点\(Q\)，用\(Q\)在投影平面投影的\(Q^{'}\)来代表\(R\)​的投影。从双力偶点源地震波辐射的空间的对称性考虑，这样做是可以的。由于这种投影将球面上的点与极点相连，投影到赤平面上，这种投影又称为极射赤平面投影。

图3 Wulff 投影的表示

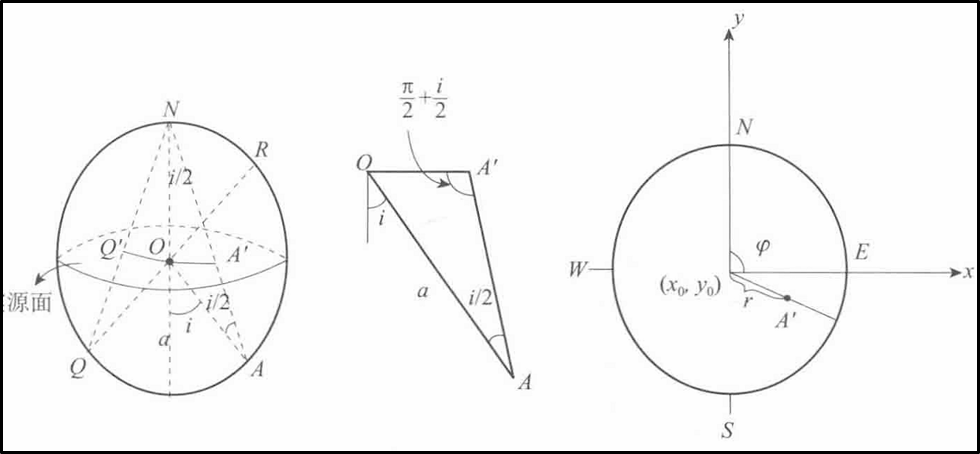
​ 球面上\(A\)点的空间方位是由矢径的方位角\(\varphi\)和离源角\(i\)确定的。\(A\)在投影网上的投影点为\(A^{'}\) 的位置也是通过这两个角度来确定的。\(\varphi\) 从网的正北标记随时针方向的度量(\(0^{o} \sim 360^{o}\))。与\(i\)对应的线段\(OA^{'}\)的长度\(r\)可以由下述的方法确定：\(OAA'\) 的角度为\(90^{o}+i/2\) ,\(OA\) 的长度为半径\(a\)，则在三角形\(OAA'\)​ ,根据正弦定理有

\[\frac{r}{{\sin \left( {\frac{i}{2}} \right)}} = \frac{a}{{\sin \left( {\frac{\pi }{2} + \frac{i}{2}} \right)}} \]

可以得到：

\[r = a\tan \left( {\frac{i}{2}} \right) = a\frac{{1 - \cos i}}{{\sin i}} \]

这种投影即为\(Wulff\) 网投影，这种是一种等角投影，球面上的曲线的交角投影到平面上后保持不变，球面上的圆投影到平面后依然是一个圆。根据上图的分析可知，投影点距\(Wulff\) 网中心越近，离源角越小，投影点越靠近投影圆的边缘，离源角越大。

​ 在进行计算机绘图时，通常以东向方向为\(x\)坐标，北向方向为\(y\)坐标，假定震源球球心为\((x_{0},y_{0})\) ，则对应于射线的方位角为\(\varphi\) 的射线\(OA\), \(A'\) 在震源平面的坐标为：

\[\left\{\begin{array}{l} x_A=x_0+a \tan \left(\frac{i}{2}\right) \sin \varphi \\ y_{A^{\prime}}=y_0+a \tan \left(\frac{i}{2}\right) \cos \varphi \end{array}\right. \]

上面说明了一条射线与震源球的交点如何在Wulff网中表示，下面说明如何将一个平面（断层面）投影到Wulff网上。如图所示，\(\pi\)断层面，阴影部分的大圆所在平面为赤平面，大圆为赤道。\(N,S,W,E\) 分别表示北、南、西、东。根据上面所讲的的单点在\(Wulff\)网上的投影，平面在赤平面的投影为一个弧，断层面上的直线\(L\)​ 投影到赤平面上为一个点。断层面投影弧的顶点到赤道的角度即为断层面的倾角。

图4 断层面π在Wulff网上的投影图示

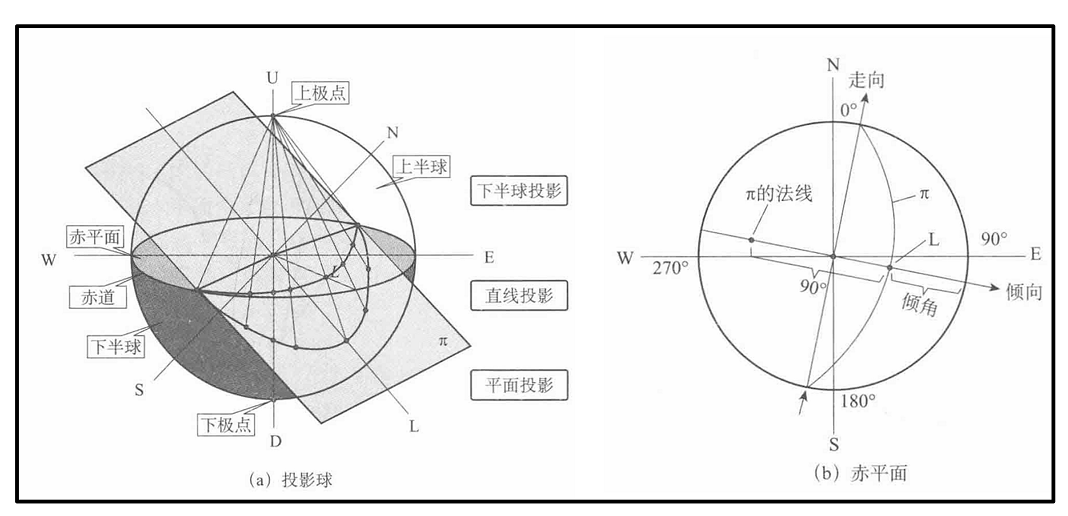
上面只是给出一个图示，如何精确将断层面表示在\(Wulff\) 网上呢？下面给出具体的公式。如图所示，假设断层面的倾角为\(\delta\) ,断层面与震源球相交一个圆\(ADBC\), 这个圆的最深点为\(A\), 最浅点为\(B\)，则\(A,B\)两点在\(Wulff\) 网上投影点的坐标可以按照上式给出。则\(A\)点对应于上图中的\(i/2\) 角为\(i/2=(\pi/2-\delta)/2=\pi/4-\delta/2\) ,\(B\)点对应于上上图中的\(i/2\)角在图10-5-4中\(i/2=(\pi/2+\delta)/2=\pi/4+\delta/2\) 。假设断层面的走向为\(\phi\) ,则\(OA\)的方位角可以表示为\(\phi+pi/2\)，\(OB\) 的方位角为\(\phi-\pi/2\) 。这样代入可以得到\(A\)和\(B\)点在Wulff 网上的投影点坐标为

\[\begin{aligned} & \left\{\begin{array}{l} x_{A^{\prime}}=x_0+a \tan \left(\frac{\pi}{4}-\frac{\delta}{2}\right) \sin \left(\phi+\frac{\pi}{2}\right) \\ y_{A^{\prime}}=y_0+a \tan \left(\frac{\pi}{4}-\frac{\delta}{2}\right) \cos \left(\phi+\frac{\pi}{2}\right) \end{array}\right. \\ & \left\{\begin{array}{l} x_{B^{\prime}}=x_0+a \tan \left(\frac{\pi}{4}+\frac{\delta}{2}\right) \sin \left(\phi-\frac{\pi}{2}\right) \\ y_{B^{\prime}}=y_0+a \tan \left(\frac{\pi}{4}+\frac{\delta}{2}\right) \cos \left(\phi-\frac{\pi}{2}\right) \end{array}\right. \end{aligned} \tag{3} \]

图5 断层面在Wulff网上的投影

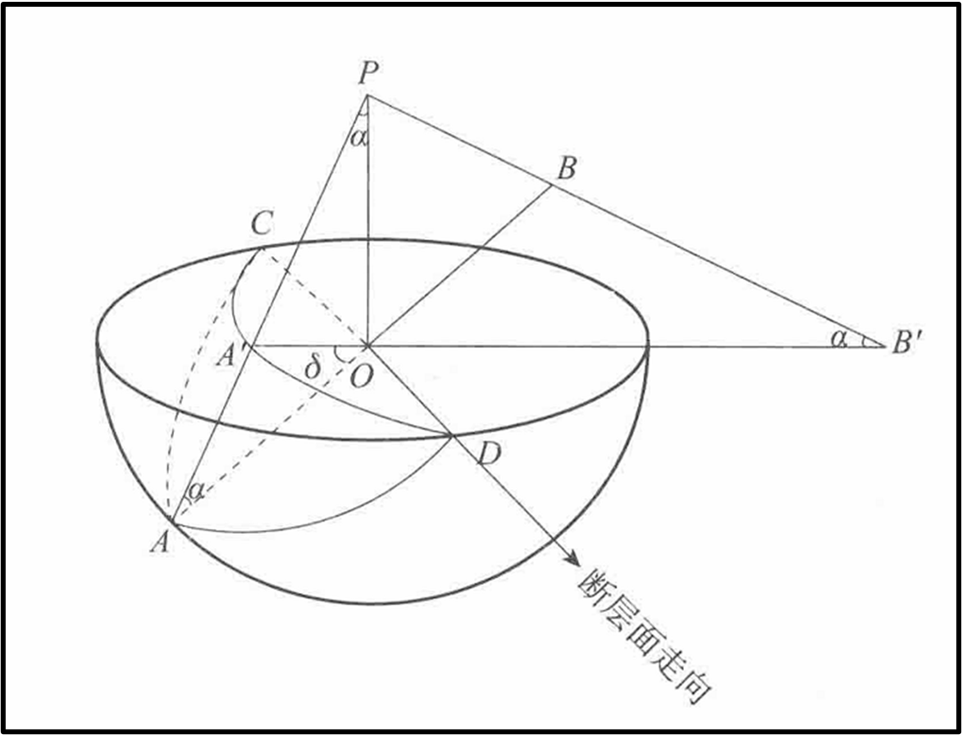
容易想象，大圆\(ADBC\)在\(Wulff\) 平面中的投影\(A'DB'C\) 依然是一个圆，倾向线\(OB\) 和\(OA\) 的投影\(B'\)和\(A'\) 是投影大圆的的两个直径的两端点。大圆的圆心\(P\)的坐标可以表示为

\[\left\{\begin{array}{l} x_P=\frac{x_{A^{\prime}}+x_{B^{\prime}}}{2} \\ y_P=\frac{y_{A^{\prime}}+y_{B^{\prime}}}{2} \end{array}\right.\tag{4} \]

现在研究大圆\(A'DB'C\) 的半径与断层倾角的关系。由上图可知，断层倾角\(\delta\) 与\(\alpha\)的关系为\(\delta=90^o-2\alpha\) ,因此，\(cos(\delta)=cos(90-2\alpha)=2sin(\alpha)cos(\alpha)\) ,将\(sin\alpha=PA'/A'B',cos\alpha=OP/PA'=a/PA'\) ,\(A'B'\) 即为大圆\(A'DB'C\) 的半径，由此可以得到投影半圆的半径为：

\[R_P=\frac{a}{\cos \delta} \]

平面\(ADBC\) 的下半球投影\(CA'D\) 是一段圆弧，此圆弧的端点\(C\) 的坐标为\((x_{0}+asin\phi,y_{0}+acos\phi)\), \(D\)的坐标为\((x_{0}-asin\phi,y_{0}-acos\phi)\) 。

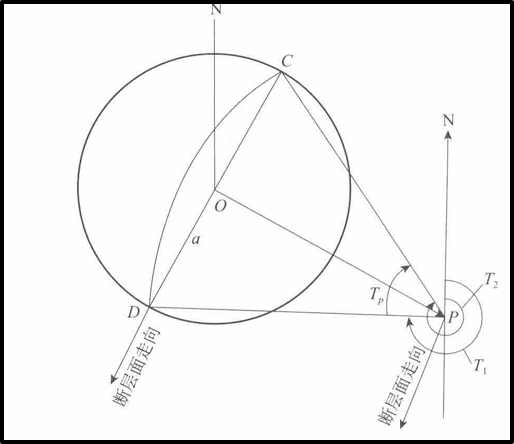
​ 在平面坐图时，\(Wulff\)网边以大圆是以\((x_{0},y_{0})\) 点为圆心，半径为\(a_{0}\) 的圆，节线则是以\((x_{p},y_{p})\) 为圆心，\(R_{p}\) 为半径的圆弧的一部分，\(Wulff\)大圆的圆心为\(CD\)的中点，\(OP\) 为线段\(CD\) 的中垂线，\(OP\)的距离为

\[\overline{O P}=\sqrt{\left(x_0-x_P\right)^2+\left(y_0-y_P\right)^2} \tag{6} \]

则根据图的几何关系，节面\(CD\)对点\((x_{p},y_{p})\) 的张角可以表示为：

\[T_P=2 \tan ^{-1}\left(\frac{a}{\overline{O P}}\right) \tag{7} \]

找到圆心P的坐标\((x_{p},y_{p})\) 以及半径\(R_{p}\) 后，还要求出画节线的圆弧的起使角度\(T_{1}\) 和终止角度\(T_{2}\) （均从正北顺时针记）。则根据图有

\[T_1=\phi+\frac{\pi}{2}-\frac{T_P}{2}, T_2=T_1+T_P \tag{8} \]

这样，以坐标\((x_{p},y_{p})\)为圆心，以\(R_{p}\) 为半径，以\(T_{1}\)为起始角，以\(T_{2}\)为终止角，绘制弧线即可得到平面的\(Wulff\)​ 投影。

​ 根据，断层面\(DAC\)的投影为弧线\(DA'C\)，断层的倾角\(\delta\) 越大，\(A'\)点越靠近直径\(DC\) ,\(\delta\) 最大为\(\pi/2\)，此时\(A'\)在直径\(DC\)上；倾角越小，\(A'\) 越靠近投影圆的边缘，倾角最小为0，此时\(A'\) 在投影\(Wulff\)​ 圆上。

图6 节线与Wulff大圆的半径

​ 前面讲到了断层的走向和倾角如何表示在\(Wulff\) 网上。 此了断层走向和倾角外，描述断层滑动性的参数还有滑动角，如何将滑动角表现在\(Wulff\) 网上呢? 首先看一看滑动角为负（即正断层类型）的情况。可以把弧长表示的断层的弧分为\(0^o\sim -180^0\),如果 断层中靠近表示中靠近表示走向的弧的端点并向外滑动，则表示纯左旋滑动，滑动角\(0^o\)；弧的中点向外滑动的矢量对应于滑动角为\(-90^0\)的情况，为纯正断层滑动；走向反方向的弧的端点向外滑动为纯右旋滑动，对应于滑动角为\(-180\)的情况。因此，对应于正断层性质的断层可以采用在弧线的不同位置绘出向外的箭头表示出来。同样对应于滑动角为正（逆断层性质）的情况，可以把表示断层的弧分为\(0^o\sim 180^o\)，走向上的弧的端点向着圆心滑动，则表示纯右旋滑动，滑动角\(180^0\)；弧的中点的指向圆心的滑动对应于\(90^o\)的滑动角；走向反方向的弧的端点指向圆心的滑动对应于纯左旋滑动，滑动角为\(0^o\) 。因此对应于正断层性质和逆断层性质的断层均可以采用在弧线的不同位置绘出向外或向内的箭头表示出来，向外的箭头表示滑动角为负，向内的滑动表示滑动角为正。

​ 根据断层滑动的方向矢量的定义，可以知道滑动方向与\(Z\)轴夹角的方向余弦为\(-sin\lambda cos\delta\)，而滑动角与\(z\)轴夹角正是此滑动方向与\(Z\)轴夹角正是此滑动方向的偏垂角，有

\[i_h=\cos ^{-1}(-\sin \lambda \sin \delta) \tag{9} \]

将该角度带入\(Wulff\) 网的投影式，可以得到在\(Wulff\) 网的大圆离圆心的距离。除了该参数外，还需要知道方位角才能得到该点在\(Wulff\) 网上的投影。为得到\(\phi\)，研究球面直角三角形，根据球面直角三角形的边角关系的公式，有

\[\cos \lambda=\cos \delta \cos \varphi \tag{10} \]

因此有

\[\varphi=\cos ^{-1}\left(\frac{\cos \lambda}{\cos \delta}\right) \tag{11} \]

根据前面的讲解，远震数据能够得到的地震矩张量通常简化为双力偶进行描述。仅根据远场观测数据很难确定哪个节面为真实的地震断层面。通常描述该类震源将两个节面均在\(Wulff\) 网中绘出，并且给出其膨胀象限和压缩象限，这类震源机制的投影图形通常称作沙滩球(beach ball)。需要采用参数转换将震源机制的一个节面的参数转换为另外一个节面的参数。

​ 得到两个节面的走向、倾角和滑动角后，需要找到膨胀象限的区域范围。首先找到两条节线所加的\(Wulff\) 投影的弧所包围的区域边界。应该先找到两条节线所加的\(Wulff\) 投影圆的弧。如果两个节面走向分别为\(\phi_{1}\),\(\phi_{2}\) ,则可以\(\phi_{1}+\pi\)和\(\phi_{2}\) 所夹的弧以及\(\phi_{2}+\pi\)和\(\phi_{1}\) 所夹的弧以及两个节面所围成的区域处于相同的压缩区或者膨胀区。如果滑动角大于零，则有逆冲分量，此时该区域内为膨胀区，应该填充颜色；而其他区域不填充颜色；反之，如果滑动角小于零，表面有正断层分量，此时该区域内为压缩区，不应填充颜色，而其他区域填充颜色。其他区域定义为所有的 圆形区域即可。

震源机制沙滩球绘制的MATLAB代码\(focalmech.m\)​

function focalmech(fm, centerX, centerY, diam, varargin)
%	>> focalmech(fm, centerX, centerY, diam, varargin)
%   Draws full moment tensor beachball diagram of earthquake focal mechanism.
%   Required inputs
%	fm: 3x3 or 1x6 vector of the six independent components of the 
%           moment tensor (mrr, mtt, mff, mrt, mrf, mtf).
%	centerX, centerY: position to place beachball at position
%	diam: diameter of drawn beachball.
%
%	Optional inputs
%	color for tensional region changed by 'r', 'g', 'b', 'y', 'm', 'c' or 
%       3 element color vector. default is black.
%   scalar argument is assumed to be an aspect ratio for non-equal axes.
%       Value is stretch in E-W direction.
%       'map' or 'Mercator' will do automatic Mercator aspect ratio
%       assuming centerY = lat
%   'dc' will force to best fitting double-couple solution
%   'nofill' will leave transparent (nodal lines only)
%   'text' will add following argument as a title to the beachball
%   'FontSize' with following argument will change fontsize for text
%
%   Written to give a MatLab equivalent of psmeca -Sm from GMT.
%   As such, this function requires a moment tensor. For planes (e.g.,
%   strikes and dips), use bb.m. bb is a nice beachball plotting function
%   from Oliver Boyd at CERI, but aimed strictly at double-couple
%   mechanisms.
%
%   Written by James Conder, Southern Illinois University, Jan 10, 2017
%   Please cite:
%   Conder, J.A. and C.A. Arciniegas, Conjugate Faulting in the Wabash
%       Valley Fault Zone exhibited by the Nov 20, 2012 M3.6 earthquake, 
%       a Mt Carmel Late Aftershock, Seismological Research Letters, 88,
%       1203-1209, doi:10.1785/0220170021, 2017
%
%   2/20/2017 realized that a vertical vector may not actually be within
%   a single contour if there is a large isotropic component.
%   Algorithm changed to using sign of vector explicitly inside contour.
%   3/12/2017 Vectorized main loop to improve efficiency.
%   (Speed gains of 4-10x).

% defaults
fillcolor = [0 0 0];  % black for tensional region(s)
unitratio = 1;      % axis equal
DC = false;         % show non double-couple components
colorit = true;     % fill in tensional regions
ctitle = [];        % text above beachball
fsize = 10;         % fontsize for text

% set parameters based on varargin inputs
if nargin > 4
    icheck(1:nargin-4) = true;
    for i = 1:nargin-4
        if icheck(i)
        if isnumeric(varargin{i})
            if isscalar(varargin{i})
                unitratio = varargin{i};
            end
            if length(varargin{i}) == 3
                fillcolor = varargin{i};
            end
        elseif ischar(varargin{i})
            switch varargin{i}
                case {'r'}
                    fillcolor = [ 1 0 0 ];
                case {'g'}
                    fillcolor = [ 0 1 0 ];
                case {'b'}
                    fillcolor = [ 0 0 1 ];
                case {'y'}
                    fillcolor = [ 1 1 0 ];
                case {'m'}
                    fillcolor = [ 1 0 1 ];
                case {'c'}
                    fillcolor = [ 0 1 1 ];
                
                case {'map','Map','mercator','Mercator'}
                    unitratio = 1/cos(centerY*pi/180);
                    
                case {'dc','DC','double-couple','doublecouple'}
                    DC = true;

                case {'nocolor','nofill','transparent'}
                    colorit = false;

                case {'text','title'}
                    ctitle = varargin{i+1};
                    icheck(i+1) = false;

                case {'fontsize','FontSize','Fontsize','fsize'}
                    fsize = varargin{i+1};
                    icheck(i+1) = false;
            end 
        end
        end
    end     
end

%colormap([1 1 1; fillcolor])    % 2 color beachball fill   % 注释掉，默认为黑白球
sE = unitratio*0.5*diam; sN = 0.5*diam; % scaling for plotting
u = sE*cos(0:0.02:2*pi); w = sN*sin(0:0.02:2*pi);   % reference circle


%%% put fm (A&R convention, rtf) into 3x3 cartesian (xyz)
%%% x = north, y = East, Z = down (Aki & Richards pg 113)
M = eye(3);
if length(fm) == 6
   M(1,1) = fm(2); M(2,2) = fm(3); M(3,3) = fm(1);
   M(2,1) = -fm(6); M(1,2) = M(2,1);
   M(3,1) = fm(4); M(1,3) = M(3,1);
   M(3,2) = -fm(5); M(2,3) = M(3,2);
else
   M(1,1) = fm(2,2); M(2,2) = fm(3,3); M(3,3) = fm(1,1);
   M(2,1) = -fm(3,2); M(1,2) = M(2,1);
   M(3,1) = fm(2,1); M(1,3) = M(3,1);
   M(3,2) = -fm(3,1); M(2,3) = M(3,2);
end
    
% Tensional and compressional regions are determined by sign of 
%   local 'radius'.
% Negative length = compression, and positive length = tension
% Length is found by linear combination of three eigen vectors.

% find eigenvalues and eigenvectors of system and put in descending order
[V,D] = eig(M);
D = diag(D);
eig1 = max(D);      % largest eigenvalue
eig3 = min(D);      % smallest eigenvalue
if eig1 == eig3
    eig2 = eig1;
    i1 = 1; i2 = 2; i3 = 3;
else
    i1 = find(D == eig1,1);
    i3 = find(D == eig3,1);
    i2 = 6 - i1 - i3;
    eig2 = D(i2);
end

vT = V(:,i1);       % eigenvectors: TBP
vB = V(:,i2);
vP = V(:,i3);

% check for explosions or implosions
if eig1 <= 0     % implosion
    fill(centerX+u,centerY+w,'w')   % fill white circle
    return
end
if eig3 >= 0     % explosion
    fill(centerX+u,centerY+w,fillcolor)   % filled circle
    return
end

%%% if forced to be double couple
if DC
    eigB = 0.5*(eig1 - eig3);
    eig1 = eigB; eig2 = 0; eig3 = -eigB;
end

% Sweep out hemisphere to find negative & positive regions
dx = 0.02; dy = dx;     % grid loop
x = -1:dx:1; y = -1:dy:1;
nx = length(x); ny = length(y); % vectorization of previous code begins here
vij = zeros(3,nx,ny);

x2 = repmat(x',1,ny);
y2 = repmat(y,nx,1);
r2 = x2.*x2 + y2.*y2;        
trend = atan2(y2,x2);
plunge = pi/2 - 2*asin(sqrt(r2/2));  % equal area projection
ir = r2 > 1;
vij(1,:,:) = cos(trend).*cos(plunge);   % set up local vector grids
vij(2,:,:) = sin(trend).*cos(plunge);
vij(3,:,:) = sin(plunge);

% project eigenvectors onto local vectors
uT = 0*vij; uB = 0*vij; uP = 0*vij; 
uT(1,:,:) = vij(1,:,:)*vT(1) + vij(2,:,:)*vT(2) + vij(3,:,:)*vT(3);
uT(3,:,:) = uT(1,:,:)*vT(3);
uT(2,:,:) = uT(1,:,:)*vT(2);
uT(1,:,:) = uT(1,:,:)*vT(1);
uB(1,:,:) = vij(1,:,:)*vB(1) + vij(2,:,:)*vB(2) + vij(3,:,:)*vB(3);
uB(3,:,:) = uB(1,:,:)*vB(3);
uB(2,:,:) = uB(1,:,:)*vB(2);
uB(1,:,:) = uB(1,:,:)*vB(1);
uP(1,:,:) = vij(1,:,:)*vP(1) + vij(2,:,:)*vP(2) + vij(3,:,:)*vP(3);
uP(3,:,:) = uP(1,:,:)*vP(3);
uP(2,:,:) = uP(1,:,:)*vP(2);
uP(1,:,:) = uP(1,:,:)*vP(1);

% get weights for each eigenvector across hemisphere space
wT = uT(1,:,:).*uT(1,:,:) + uT(2,:,:).*uT(2,:,:) + uT(3,:,:).*uT(3,:,:);
wB = uB(1,:,:).*uB(1,:,:) + uB(2,:,:).*uB(2,:,:) + uB(3,:,:).*uB(3,:,:);
wP = uP(1,:,:).*uP(1,:,:) + uP(2,:,:).*uP(2,:,:) + uP(3,:,:).*uP(3,:,:);

uz = wT*eig1 + wB*eig2 + wP*eig3;   % lengths grid
uz = squeeze(uz); uz(ir) = nan;
clear vij uT uB uP wT wB wP

%%% plot
% Note centerX & centerY are in conventional cartesian coords unlike x,y
% above where x is north.
hold on
if ~colorit
    plot(centerX+u,centerY+w,'k')   % plot circle boundary
    c = contourc(centerX+sE*y,centerY+sN*x,uz,[0 0]);       % no fill
    i = c(2,:) >= 1;
    c(:,i) = nan;
    plot(centerX+sE*c(1,:),centerY+sN*c(2,:),'color',fillcolor)   % plot circle boundary    
else
    fill(centerX+u,centerY+w,'w')   % fill white circle
    plot(centerX+u,centerY+w,'k')   % plot circle boundary


% fill in tensional regions
%contourf(centerX+sE*y,centerY+sN*x,uz,[0 0]);   % fill in tensional regions
% Need to use 'fill' as contourf will change pallette of entire figure

% get contours of zero level. *Should* be one or two segments
c = contourc(y,x,uz,[0 0]); c = c';

% find contour breaks
nc = 1;
[~,I] = sort(c(:,2),'descend');
if c(I(2),2) > 7
    nc = 2;
end
I = I(1:nc);

%reset c with just contours of interest (maximum of 2)
if nc == 1
    c = [ c(I(1),:); c(I(1)+1:I(1)+c(I(1),2),:)];
else
    c = [ c(I(1),:); c(I(1)+1:I(1)+c(I(1),2),:); ...
          c(I(2),:); c(I(2)+1:I(2)+c(I(2),2),:)];
end
i = find(c(:,2) > 2);  % indices of contour breaks

% fill tensional regions
if nc == 1       % 1 contour (closed unless single vertical plane)
    c(1,:) = [];        % remove contour header 
    % closed contour must have vertical plunge in it - check for sign
    % not necessarily true if large isotropic component - fix
    
    % check for single vertical plane
    d2 = (c(1,1)-c(end,1))^2 + (c(1,2)-c(end,2))^2;
    
    if d2 > 2 % single vertical plane
        ang = atan2(c(end,2),c(end,1));     % location of contour end 
        dang = 0.1;
        vij = [ sin(ang+dang) cos(ang+dang) 0];
        uT = dot(vij,vT)*vT; wT = norm(uT)^2;
        uB = dot(vij,vB)*vB; wB = norm(uB)^2;  
        uP = dot(vij,vP)*vP; wP = norm(uP)^2;
        uvc = wT*eig1 + wB*eig2 + wP*eig3;
        if uvc > 0       
            a1 = (ang:0.02:ang+pi)';    % ccw along edge
        else
            a1 = flipud((ang-pi:0.02:ang)');    % cw along edge
        end   
        ac = [cos(a1) sin(a1)];
        c1 = [c; ac];
        fill(centerX+sE*c1(:,1),centerY+sN*c1(:,2),fillcolor)  
    else        % single closed contour
        xi = mean(c(:,1)); yi = mean(c(:,2)); % spot inside contour
        trend = atan2(xi,yi);   % x = north...     
        r2 = xi*xi + yi*yi;        
        plunge = pi/2 - 2*asin(sqrt(r2/2));  % equal area projection        
        vij(1) = cos(trend)*cos(plunge);
        vij(2) = sin(trend)*cos(plunge);
        vij(3) = sin(plunge);

        uT = dot(vij,vT)*vT; wT = norm(uT)^2;
        uB = dot(vij,vB)*vB; wB = norm(uB)^2;  
        uP = dot(vij,vP)*vP; wP = norm(uP)^2;
        uv = wT*eig1 + wB*eig2 + wP*eig3;
    
        if uv > 0   % fill inside contour
            fill(centerX+sE*c(:,1),centerY+sN*c(:,2),fillcolor)
        elseif uv < 0   % fill outside contour
            fill(centerX+u,centerY+w,fillcolor)
            fill(centerX+sE*c(:,1),centerY+sN*c(:,2),'w') 
        end
    end
else                    % 2 contours
    % find 4 spots where contours touch edge
    ia = ([ 2 i(2)-1 i(2)+1 length(c)])';
    dang = 0.02*pi;
    
    % determine whether contours bound positive or negative regions
    % get mid contour vector
    p1 = c(3,:);
    p2 = c(ia(2)-1,:);
    pmid = 0.5*(p1 + p2);
    ang = atan2(pmid(2),pmid(1));
    vij = [ sin(ang) cos(ang) 0]; 
    uT = dot(vij,vT)*vT; wT = norm(uT)^2;
    uB = dot(vij,vB)*vB; wB = norm(uB)^2;  
    uP = dot(vij,vP)*vP; wP = norm(uP)^2;
    uvc = wT*eig1 + wB*eig2 + wP*eig3;
        
    % first contour ending spot
    p2 = c(ia(2),:);
    ang2 = atan2(p2(2),p2(1));

    % angle between contour ends
    p1 = c(2,:);
    p2 = c(ia(2),:);
    ang = acos(dot(p1,p2)/(norm(p1)*norm(p2)));
    
    % determine direction to trace along edge
    d1 = acos(dot(vij,[sin(ang2+dang) cos(ang2+dang) 0]));
    d2 = acos(dot(vij,[sin(ang2-dang) cos(ang2-dang) 0]));
    if d1 < d2
        a1 = (ang2+0.01:0.02:ang2+ang-0.01)';    % ccw along edge
    else
        a1 = flipud((ang2-ang+0.01:0.02:ang2-0.01)');    % cw along edge
    end
        
    ac = [cos(a1) sin(a1)];
    c1 = [c(2:ia(2),:); ac; c(2,:)];
    if uvc < 0
        fill(centerX+u,centerY+w,fillcolor)   % fill colored circle
        fill(centerX+sE*c1(:,1),centerY+sN*c1(:,2),[ 1 1 1]) 
    else
        fill(centerX+sE*c1(:,1),centerY+sN*c1(:,2),fillcolor)
    end
     
    % second contour ending spot
    p2 = c(end-1,:);
    ang2 = atan2(p2(2),p2(1));
    
    % mid contour vector
    p1 = c(ia(3)+1,:);
    p2 = c(ia(end)-1,:);
    pmid = 0.5*(p1 + p2);
    ang = atan2(pmid(2),pmid(1));
    vij = [ sin(ang) cos(ang) 0]; 

    % angle between contour ends
    p1 = c(ia(3),:);
    p2 = c(end,:);
    ang = acos(dot(p1,p2)/(norm(p1)*norm(p2)));
    
    % determine direction to trace along edge
    d1 = acos(dot(vij,[sin(ang2+dang) cos(ang2+dang) 0]));
    d2 = acos(dot(vij,[sin(ang2-dang) cos(ang2-dang) 0]));
    if d1 < d2
        a1 = (ang2+0.01:0.02:ang2+ang-0.01)';    % ccw along edge
    else
        a1 = flipud((ang2-ang+0.01:0.02:ang2-0.01)');    % cw along edge
    end    

    ac = [cos(a1) sin(a1)];
    c2 = [c(ia(3):end,:); ac; c(ia(3),:)];
    if uvc < 0
        fill(centerX+sE*c2(:,1),centerY+sN*c2(:,2),'w')        
    else
        fill(centerX+sE*c2(:,1),centerY+sN*c2(:,2),fillcolor)
    end        

end
end

if ~isempty(ctitle)
    text(centerX,centerY+sN*1.1,ctitle,'HorizontalAlignment','center','FontSize',fsize)
end

end

​ 在日常工作中，通常分析别人给出的震源沙滩球，通过沙滩球分析该处地震破裂的类型和机制。如果仅给出一副沙滩球的图，如何从中读取断层的各个参数呢？下面结合上面的例子给予说明。

​ （1）根据两个节面表示弧线的凸向方向确定两个节面的走向。

​ （2）根据两个节面在\(Wulff\) 网的弯曲程度估计两个节面的倾角。

​ (3) 根据两个节面在\(Wulff\) 网上的交点\(B\)，在两个节面上找到距交点\(B\)相差\(90^o\) 的点(\(A点\))，如果\(Wulff\) 网心的区域为阴影区，则断层节线起始点(走向的反方向)到该滑动方向点(\(A\)点)的角距离即为滑动角。对于滑动角取负的情况，则断层节线结束点（走向方向）到该滑动方向点(\(A\)点)的角距离的负值即为滑动角。这样通过上面三个步骤即可以估计沙滩球所表示的两个节面的各个参数了。

​ 采用\(Wulff\)投影，投影关系简单，但在表示球面上的图形时，网心部分过于集中，边缘部分则过于稀疏。克服这种缺陷的施密特(Schmidt)投影是一种等面积投影，即球面上面积相等的区域投影到平面上后保持面积相等。采用该投影，网上的图形分布相对比较均匀。下面介绍这种投影。

3.2 等面积投影(Schmidt 投影)

​ 根据等面积投影的要求，投影震源球上的面积和投影到大圆上面积的比例为常数。我们知道，震源下班球的总面积为\(2\pi a^2\)球的面积公式为\(\pi a^2\)，因此，一般将比例常数取为2。按照下图，在震源球面上取一个半径为\(asin(i)\)，宽为\(ds\)的一个环带，而投影到大圆上为宽度为\(dp\) 的一个环。如果也按照上面的比例常数投影，则\(ds=2dp\) ,由于\(ds=2\pi(asini)adi\) ,则\(dp=2\pi rdr\) ,这样有\(2\pi(asini)adi=2(2\pi rdr)\) ，则\(a^2sinidi=2rdr\) ,对两边进行积分得到：\(-a^2cosi=r^2+C\)。我们知道\(i=0\)时\(r=0\) ,当\(i=\pi/2\)时\(r=a\), 代入积分结果表达式可得到常数\(C=a^2\)。这样可以得到：

\[r=a \sqrt{1-\cos i} \tag{12} \]

表达为：

\[r=a \sqrt{2} \sin \frac{i}{2} \tag{13} \]

可见这种投影的面积与震源球上的面积成比例，因此这种投影叫做等面积投影(等积投影)，又叫Schmidt投影。而式（13）为Schmidt投影。而式（13）为Schmidt投影半径与离源角\(i\)的关系。

​ 在表达\(Schmidt\) 投影时，通常根据已经介绍过的\(Wulff\) 投影进行归算。已知在\(Wulff\) 网上的投影点的坐标\(x_{w},y_{w}\)，则其方位角：

\[\varphi=\tan ^{-1} \frac{x_{\mathrm{w}}-x_0}{y_{\mathrm{w}}-y_0} \tag{14} \]

\((x_{0},y_{0})\) 为中心点坐标。投影点距\(Wulff\) 网中心的距离为

\[R=\sqrt{\left(x_{\mathrm{w}}-x_0\right)^2+\left(y_{\mathrm{w}}-y_0\right)^2} \tag{15} \]

则根据式(13)可知该投影点的离源角为：

\[i_h=2 \tan ^{-1} \frac{R}{a} \tag{16} \]

然后采用（13）式可以得到该点的等面积投影。将一个断层面的各个投影点连起来构成了等面积投影的节线。

​ 根据\(Wulff\) 网表示滑动角的分析，还可以将断层面的滑动角自\(0^o\sim -180^o\) 取值，计算每个滑动角对应的滑动矢量的离源角\(i_{h}\) ，按式（13），并得到在\(Wulff\)​ 网上的投影点的方位角。采用得到的滑动矢量离源角，计算Schmidt投影的各个滑动矢量在大圆上距圆心的距离，再根据前面得到每个滑动矢量的投影点，将这些投影点连接起来即为该断层面的投影。这就是表示断层倾角的另一种方法。

图7 震源球和其对应断层几何形状

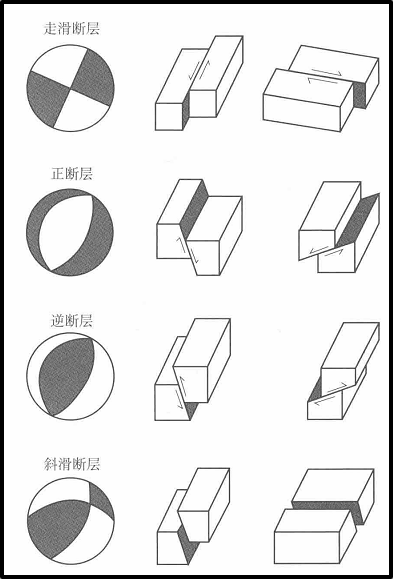
​ 为了进一步理解“沙滩球”，用图解给出了不同类型的震源机制。阴影区表示\(P\)波射线从震源向外离开震源，在接受台站处产生向上的初动，而非阴影区将导致接受台站产生向下的初动。拉张轴在阴影区的中部，压缩轴在非阴影区的中部。通常用“沙滩球”的中部是白色还是黑色来识别是正逆断层，如果中部白色（非阴影），边缘黑色（阴影区），则表示正断层；反之，若中部黑色（阴影区），边缘白色（非阴影区），则表示逆断层。