LTE Basic Procedure
本文翻译自http://www.sharetechnote.com/
MIMO(Multiple Input Multiple Output)
基础概念
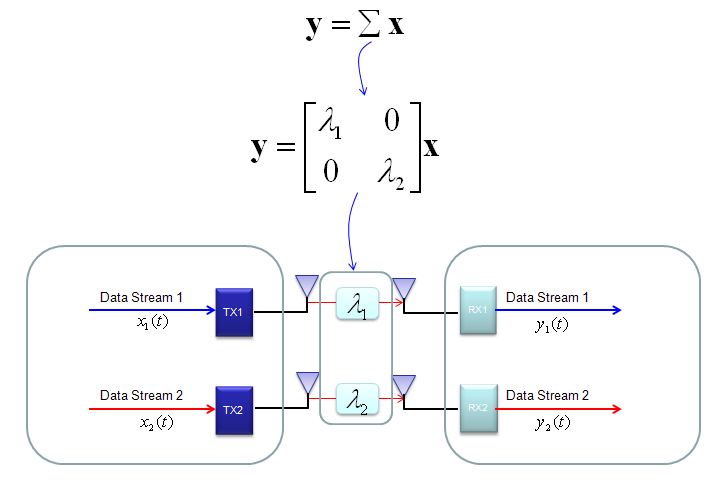
如图所示，在MIMO中，多个独立的数据流同时传输，因此与SISO（单输入单输出）情况相比，它可以实现更高的数据吞吐量。然而，与SISO情况相比，在数据传输的可靠性（例如，误差较小）方面几乎没有优势。
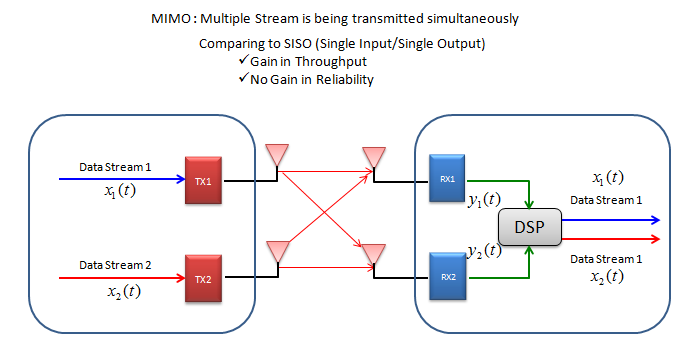
还有一个概念经常与MIMO混淆。这就是分集。MIMO和分集有什么区别？
下图将展示分集的概念。基本上有两种类型的分集，称为接收器分集和发射器分集。
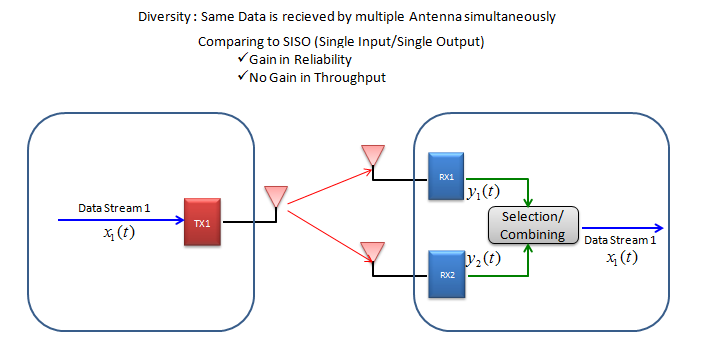
如图中所示，在这种分集配置中，一个比特流的一个副本正在被传输，并通过稍微不同的路径到达多个接收器天线，这意味着接收器可以具有相同数据的多个版本。在多个版本中，接收者可以选择最好的一个，或者以这样的方式将它们组合在一起，以提高数据质量。通过这样做，可以提高通信可靠性（减少错误）。但在数据吞吐量方面没有优势。
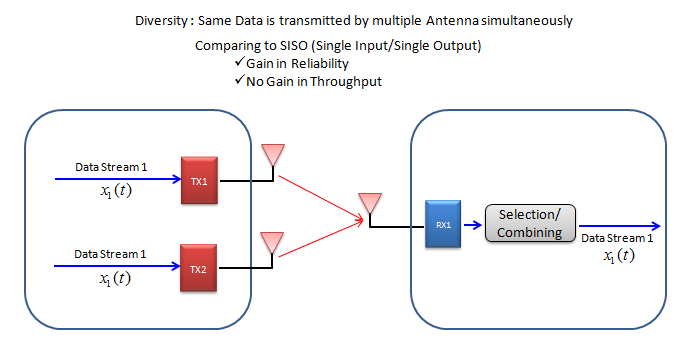
下图是另一种分集。在这种分集配置中，一个（单个）比特流的多个副本通过多个Tx天线传输，并通过稍微不同的路径到达单个接收器天线，这意味着接收器可以具有相同数据的多个版本。在多个版本中，接收者可以选择最好的一个，或者以这样的方式将它们组合在一起，以提高数据质量。通过这样做，可以提高通信可靠性（减少错误）。但在数据吞吐量方面没有优势。
然而，如果想知道MIMO/分集的细节，尤其是物理层发生的事情，如果不通过基础数学，几乎不可能理解MIMO/分集概念的细节。事实上，数学本身并没有那么复杂，但解释数学并将其转化为实际实现是很困难的。参见工程数学矩阵。
Overall Configuration and Procedure
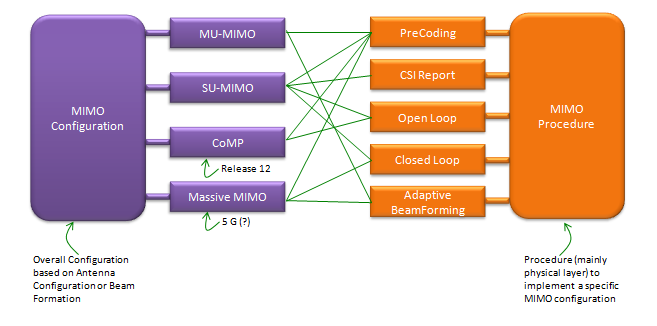
MIMO的数学模型
在2x2的情况下，整个数据传输过程可以如下所示。红色箭头和两个天线之间的四个方框用于说明两个Tx和两个Rx天线之间可能的数据路径。
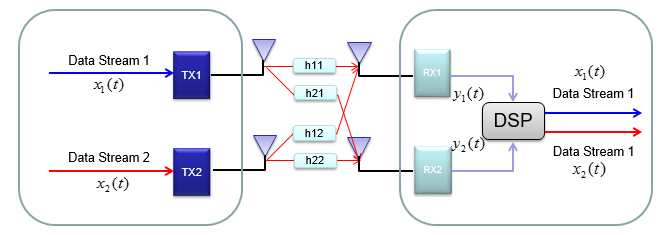
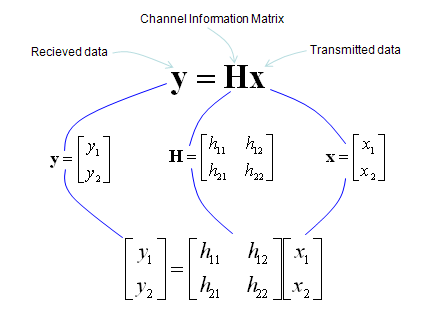
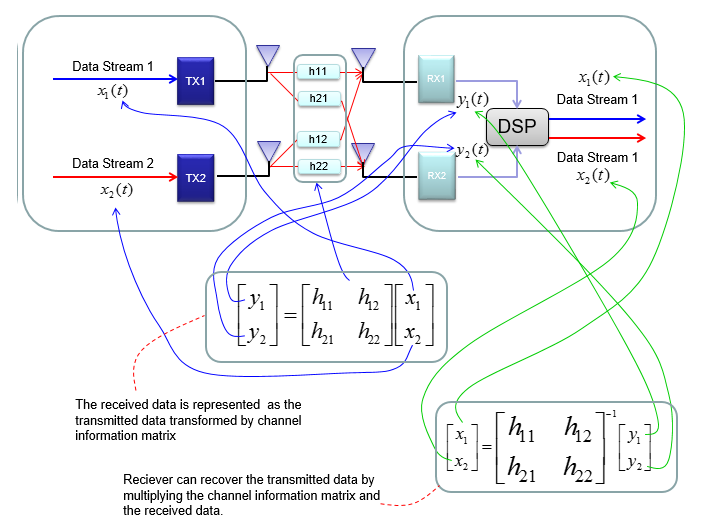
正如您在绿色箭头所示的过程中所看到的，要从接收到的数据中恢复传输的数据（原始数据），我们需要取信道信息矩阵的逆。不幸的是，这种方法有几个问题：
- 并非所有矩阵都是可逆的。有些矩阵不存在逆矩阵。（请参考这里，看看什么样的矩阵是不可逆的）。
- 计算逆矩阵不是一个简单的过程。因此，如果有某种方法来预处理数据，使得UE可以解码数据，而无需对信道矩阵进行逆矩阵计算。
为了解决这些问题，使用奇异值分解方法将信道信息矩阵转化为三个矩阵。
在工程领域应用任何数学技术时，它应该在工程意义上是有意义的，并且应该是可实施的。SVD的含义和实现如下所示。
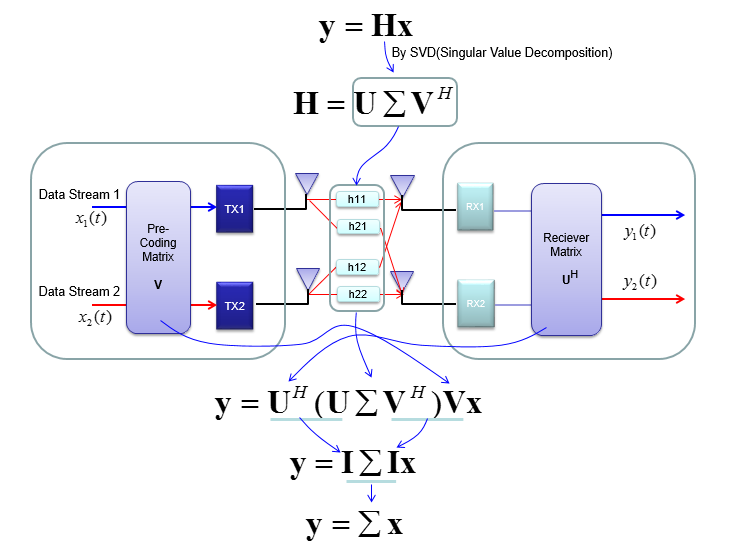
重要的是，通过实现这种方法，我们可以将信道信息矩阵表示为一个简单的“对角矩阵”。该对角矩阵如下所示，并可如下所示。它看起来不是简单明了吗？-：）
发送端如何计算预编码矩阵？
在上一节中，大致解释了如何设计（实现）预编码器。简单地说，取信道矩阵，对矩阵进行奇异值分解，然后取奇异值分解结果的酉矩阵。
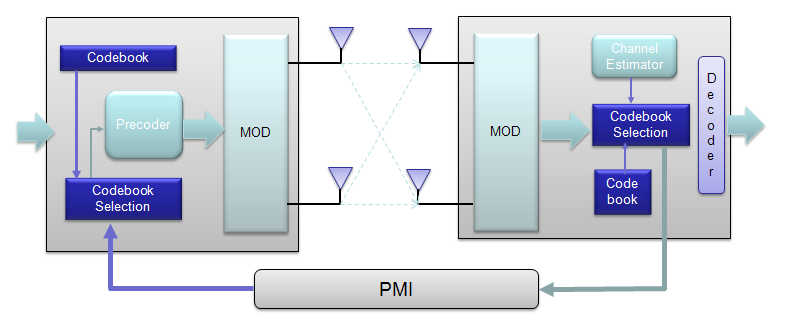
然而，在现实中，有一个关键问题没有在上面提到。在上一节中，应该给出信道矩阵以找到预编码矩阵。下一个问题是，谁（发射机或接收机）可以算出信道矩阵。它是接收机，因为接收机（在这种情况下是UE）可以基于发射机（在这种情况下是eNB）发送的特定参考信号执行信道估计。然而，在发射机（eNB）处需要预编码矩阵。
那么，发射机如何知道预编码矩阵呢？从概念上讲，最简单的方法是，接收器（UE）将整个预编码矩阵通知eNB。这仅在概念上是简单的，但实现起来并不简单，因为发送整个预编码矩阵需要相当大的带宽，这可能是一个巨大的开销。
为了解决这种开销问题，3GPP想出了一条捷径，如下所述。在这种方法中，他们根据标准化过程中对无线信道的广泛调查，预定义了一组矩阵。UE和eNB都知道这些预定义矩阵。
然后，UE基于其自身的信道估计选择特定的预编码器（预编码矩阵），并将其选择的预编码矩阵的索引通知eNB。因为这只是矩阵的索引（而不是矩阵本身），所以我们可以在不造成太多开销的情况下实现这种方法。
对于一些MIMO实现（例如，LTE中的TM4=闭环MIMO），估计信道并选择特定的预编码矩阵，然后将其发送回接收机，如下所示。
UE在特定时刻选择最适合该信道的码本的算法如下。
一旦如这里所示选择了特定的码本元素（预编码矩阵），该预编码矩阵将用于变换输入比特，如预编码部分中所述。
实际中的考虑
让我们再看看下面的数学模型。
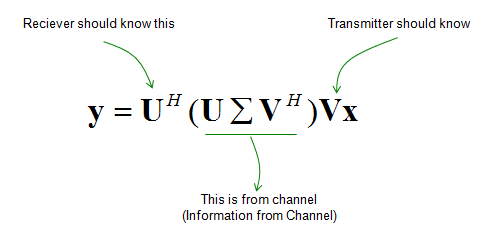
- 中心的三个矩阵至少对接收器来说是已知的，因为接收器可以根据接收到的信号估计信道矩阵，并根据信道矩阵计算这些矩阵。
- 发射机知道矢量 \(x\) ，因为它是传输的数据。
- 因为矩阵 \(U\) 可以从 \(H\) 中导出，所以它可以是接收器已知的。
问题是如何计算矩阵 \(V\) 。关于这个矩阵，有两个主要问题:
- 这是发送端应该使用的，但发送端没有关于 \(H\) 的任何信息。因此无法在发送端直接计算。
- 在传输数据（矢量 \(x\) ）之前，该矩阵在发送器端使用。发送器怎么能在事情发生之前就知道呢？
最常见的解决方案之一是，接收机分析信道矩阵 \(H\) 并通知发射机最佳矩阵 \(V\) 。这被称为“闭环MIMO”，LTE TM4（传输模式4）属于这一类。
现在这种闭环方法可以解决上面列出的所有问题吗？不幸的是没有。
问题如下：
- 虽然UE可以计算出矩阵 \(V\) ，但它是根据刚刚接收到的数据计算出来的。如果它将该信息发送给发射器，发射器将使用该信息进行下一次传输。如果当前传输和下一次传输之间的信道条件没有太大差异，那么来自接收器的这些信息将对发射机上的下一次传输有很大帮助。但是，如果信道条件变化如此之快，这些信息可能就没有用处了。
- 尽管UE计算出了正确的矩阵 \(V\) ，但将整个矩阵本身发送到发送器会带来巨大的数据量和开销。在某些情况下，比如LTE，他们使用了一种变通方法。在解决方法中，我们只使用几个/几个预定义的V矩阵，接收器评估每个候选矩阵，选择最佳的一个，并将候选矩阵的索引而不是整个矩阵内容通知发送器。例如，在LTE TM4中，他们仅为2x2 MIMO定义了4个候选V矩阵（预编码矩阵），为4x4 MIMO定义了16个候选。在数学方面，被选中的候选人可能不是最合适的人选，但在数学准确性和报告开销之间进行权衡时，它可能是最佳选择。
- 在LTE TM 8、9、10中，介绍了一种方法，通过这种方法，发射机可以使用任何预编码矩阵 \(V\) 。在这种情况下，发射机正在使用称为UE特定（接收器特定）参考信号的特殊参考信号，以帮助在接收端更好地解码。
Rank Indicator
从更实际的角度讲，秩指示符是一种数字（指示符），表示MIMO通信的工作情况。例如，假设UE正在使用2x2 MIMO配置与eNB通信，并且UE报告RI（秩指示符）为“2”，这意味着2x2 MIMO正在以真正的MIMO方式执行。然而，如果UE报告RI为“1”，则意味着通信正在进行，就像使用单天线一样。这意味着2x2 MIMO没有以最佳效率运行。
用更正式的方式解释同一件事，可以这样说：
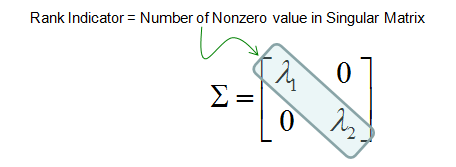
考虑奇异矩阵的定义：是一个对角矩阵。一旦得到一个信道的奇异矩阵，就可以从中提取一些非常重要的信息。
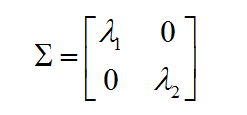
从奇异矩阵中可以得到的最重要的信息之一是秩指示符。秩指示符是指对角线元素的个数，它不是零。秩指示的物理含义是独立通信通道的数量。以2x2奇异矩阵（对于2x2 MIMO）为例，如果秩指示符为2。如下所示的两个对角线元素均为非零值，并建立了两个独立的通信管道。如果矩阵的秩指示符为1，则对角线元素（Lamda 1或Lamda 2）之一为零。这意味着，即使我们设置了两个天线，实际工作的数据流只有1，这意味着其中一个天线的信号完全丢失或被无法解码的噪声掩埋。
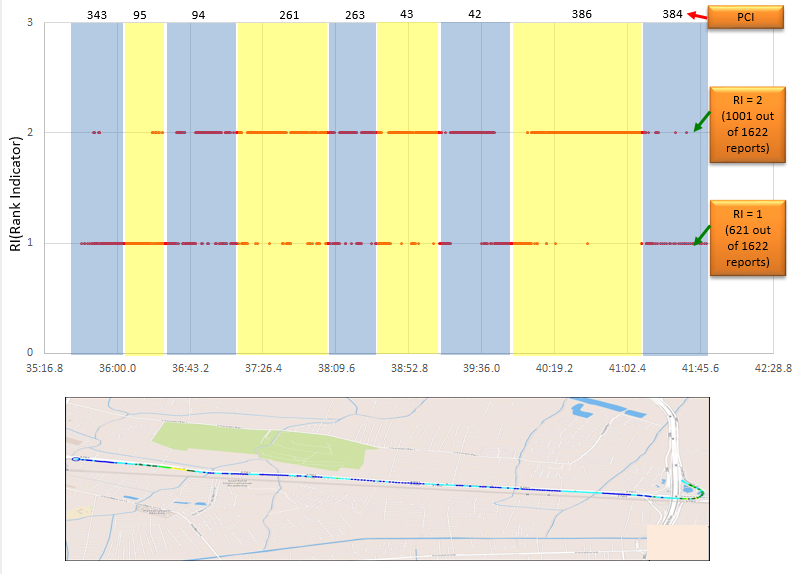
Example 1 > RI Report from a drive test on a High Way under 2x2 TM3
下面的图来自驾驶测试工具Azenqos驾驶测试工具（AZQ Android）捕获的数据。得到了工具捕获的日志，并将数据导出为csv文件，然后在Microsoft Excel上打印。底部显示测量路径的地图是AZQ reporting tool自动创建的地图。
在这个具体的例子中，会看到大量RI=1的报告，这意味着在很多情况下2x2 MIMO不能以完全的效率工作。
条件数
可能会有问题。秩指示符只关心奇异矩阵中非零值的数目。这是否意味着这些数字的多少无关紧要？例如，（lamda1=1，lamda2=1）和（lamda1=2，lamda2=0.1）之间的实际通信性能没有任何差异吗？在这两种情况下，秩指示是相同的，但实际的通信性能是不同的。因此，为了正确估计MIMO信道的实际性能，我们可能需要另一个指标，该指标是定义如下的条件数（根据参考文献[1]。强烈建议您阅读此参考文献）
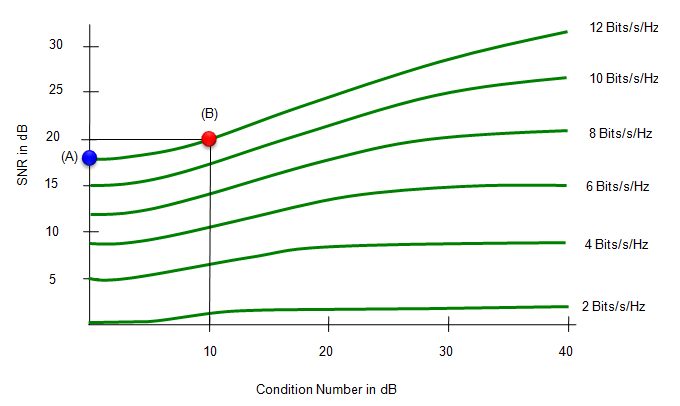
如上所述，随着对角线数之间的差异越来越小，MIMO信道工作得越理想。[1]中的下图显示了该属性。横轴以dB为单位表示条件数，纵轴以dB为单位表示信噪比。每一行显示了达到相同数据速率的情况。线上的每个点都表示“为了在特定条件下达到特定性能（数据速率），需要多少信噪比？”？或者你可以把它解释为“当你被赋予一定的条件数和一定的信噪比时，你能获得多少性能（数据速率）”。
例如，看看标记为（B）的点。这一点告诉我们，“在这个特定的通信系统中，当条件数为10 dB，信噪比为20 dB时，我们可以实现最大12位/s/Hz的数据速率”。换句话说，“要在10 dB的条件下实现12位/秒/赫兹的数据速率，我们需要至少20 dB的信噪比”。
现在来看（A）点。它告诉我们“在这个特定的通信系统中，当条件数为0dB，信噪比为16dB时，我们可以实现最大12位/s/Hz的数据速率”。换句话说，“要在0 dB的条件下实现12位/秒/赫兹的数据速率，我们需要至少16 dB的信噪比”。
如果比较（A）点和（B）点，在这两个点上，可以获得相同的性能（数据速率），但在点（A）上，我们可以实现数据速率，即使与点（B）相比，信噪比更低。换言之，当条件数接近0 dB时，我们可以在较低的信噪比下实现数据速率。
现在，看一看通道矩阵的几个例子，看看可以从中获得什么样的信息。示例矩阵本身来自参考文献[1]，我用来执行SVD的工具是参考文献[2]（Wolfram Alpha）。
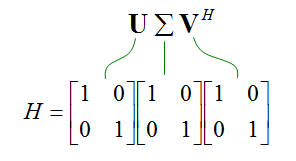
第一个例子如下。能从这个矩阵中看到发射机和接收机的物理设置吗？
因为它是2x2，所以会有两个发射器天线和两个接收器天线。它是2x2矩阵。除了对角线上的元素都是零。这意味着每个天线路径之间没有串扰。对角线上的所有元素都是“1”。这意味着来自发射器天线1的100%能量被传送到接收器天线1而没有任何损失，来自发射器天线2的100%能量被传送到接收器天线2而没有任何损失。当然，在真正的无线通信中，你永远不会遇到这种情况。但是，当你在实验室测试时，把两个无用的天线连接到测试设备上的两个通信端口，你可能会遇到这种情况。
\(H=\left[\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right]\)
现在用奇异值分解得到奇异矩阵。使用Wolfram Alpha，得到了以下结果。
现在从奇异矩阵中提取一些信息。
秩指示是2，因为对角线上非零元素的数量是2。条件数是“1”，如下所示。这意味着这是空间多路复用的完美条件，应该可以从这个通道获得最大的性能。
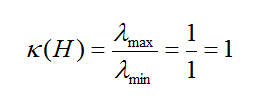
第二个例子如下。能从这个矩阵中看到发射机和接收机的物理设置吗？
因为它是2x2，所以你会有两个发射器天线和两个接收器天线。它是2x2矩阵。所有元素，甚至非对角元素，都不是零。这意味着所有可能的方式都存在串扰。矩阵中的所有元素都是相同的值，即1/sqrt（2）。这意味着来自发射器天线1的50%能量被传送到接收器天线1，来自发射器天线1的另50%能量被传送到接收器天线2。这也意味着来自发射器天线2的50%能量被传送到接收器天线1，来自发射器天线2的另50%能量被传送到接收器天线2。
\(H=\left[\begin{array}{cc}\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{array}\right]\)
现在用奇异值分解得到奇异矩阵。使用Wolfram Alpha，得到了以下结果。
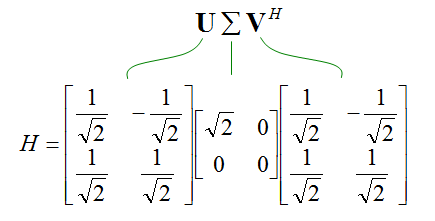
现在从奇异矩阵中提取一些信息。
秩指示是1，因为对角线上非零元素的数量只有1。
看看条件数。在纯粹的数学意义上，它无法计算，因为分母为零。但在实际意义上，你可以把“0”看作一个非常小的数字。在这种情况下，您可以得到如下所示的条件编号，这是一个非常大的数字。这意味着该信道是MIMO的最坏条件。
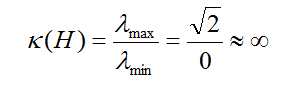
第三个例子如下。能从这个矩阵中看到发射机和接收机的物理设置吗？
因为它是2x2，所以会有两个发射器天线和两个接收器天线。它是2x2矩阵。所有元素，甚至非对角元素，都不是零。这意味着所有可能的方式都存在串扰，但对角线元素和非对角线元素之间的值有90度相移。这意味着来自发射器天线1的50%能量被传送到接收器天线1，来自发射器天线1的另50%能量以90度相移传送到接收器天线2。这也意味着来自发射器天线2的50%能量以90度相移传送到接收器天线1，来自发射器天线2的另50%能量传送到接收器天线2。这意味着两个信号从两个发射天线发射，并进入一个接收天线完全不干扰。
\(H=\left[\begin{array}{cc}\frac{1}{\sqrt{2}} & j \frac{1}{\sqrt{2}} \\ j \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{array}\right]\)
现在用奇异值分解得到奇异矩阵。使用Wolfram Alpha，得到了以下结果。
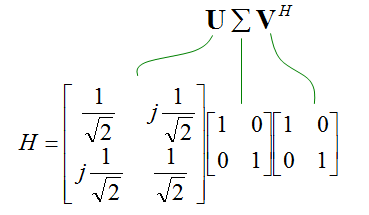
现在让我们从奇异矩阵中提取一些信息。
秩指示是2，因为对角线上非零元素的数量是2。
条件数为1，这意味着MIMO的完美条件。正如在这里看到的，尽管两条通信路径之间存在串扰。根据串扰的特性，这可能是MIMO的一个非常好的条件。有没有办法实现这种信道条件？对有。如果交叉极化天线，你可以有这种信道条件。
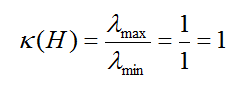
下面是另一个更现实的例子。你能从这个矩阵中看到发射机和接收机的物理设置吗？
因为它是2x2，所以会有两个发射器天线和两个接收器天线。它是2x2矩阵。所有元素，甚至非对角元素，都不是零。这意味着在所有可能的方式中都存在串扰，但要直观地知道到底有多少能量流向哪个天线并不容易。当然，你可以通过计算所有这些复数的大小和角度来计算。。但想想直觉的意义。由于所有元件的大小和角度都不相同，因此通信路径之间的串扰不会达到100%的破坏性。
\(H=\left[\begin{array}{cc}0.9+j 0.1 & 0.2-j 0.3 \\ -0.3+j 0.5 & -0.7-j 0.1\end{array}\right]\)
在这种情况下，SVD可以发挥重要作用。使用Wolfram Alpha得到如下结果。
现在让我们从奇异矩阵中提取一些信息。
秩指示是2，因为对角线上非零元素的数量是2。
条件数为1.6563，这不是MIMO的最佳情况，也不是最坏情况。以dB为单位小于3。如果你把这个数字插入到上面的图表中，这对MIMO来说是非常好的条件。
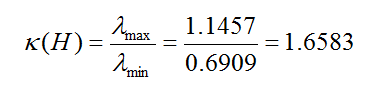
UE和网络如何计算彼此的MIMO能力？
在LTE部署的早期阶段，大多数UE只支持3类或4类。在这种情况下，假设网络和UE最多只能支持2x2 MIMO。
然而，最近（截至2017年7月），我们看到UE和网络支持2个以上的天线，并且以下所有MIMO配置正在成为一种常见能力。
- 2x2
- 4x2
- 4x4
- 8x2 (This is still not that common, but being adopted in some TDD network)
有了这些选项，网络需要知道天线配置的确切UE能力。从技术上讲，UE不需要知道网络能力，因为UE应该使用网络要求的任何东西，这取决于网络来确定UE能力，并将MIMO配置配置为不超过UE能力。然而，也有一种方法可以让UE了解网络（eNB）天线配置。
UE如何计算eNB的MIMO能力：UE可以通过检查PBCH-CRC掩码来计算eNB使用了多少天线。然而，UE只能计算出eNB正在使用的天线的数量，在达到RRC连接设置或RRC连接重新配置之前，它无法计算出网络是否可以在MIMO中使用所有这些天线，或者网络是否可以在分集中使用它们。
NW如何计算UE的MIMO能力：网络可以通过UE能力信息消息计算UE的MIMO能力。实际上，UE能力信息并不携带UE MIMO能力的任何明确信息。然而，网络可以从UE能力信息消息中报告的UE类别间接地计算出UE MIMO能力。在UE类别表中，您可以计算出可以支持的层数。根据这些信息，网络可以间接计算出UE MIMO能力。例如，如果UE类别表示UE类别支持第2层的数量，则意味着UE将支持2x2或4x2。如果UE类别表示UE类别支持第4层的数量，则意味着UE将支持4x4。
Reference
[1] Assessing a MIMO Channel - Rohde & Schwarz
[2] Wolfram Alpha
