Communication - Channel Estimation
本文翻译自http://www.sharetechnote.com/
在通信中,信号通过信道会失真,或者在信号通过信道时,会向信号中添加各种噪声。要正确地解码接收信号而不产生太多错误,就要从接收信号中去除信道施加的失真和噪声。要做到这一点,第一步是找出信号经过的通道的特性。描述信道特征的技术/过程称为“信道估计”。这个过程将如下图所示。
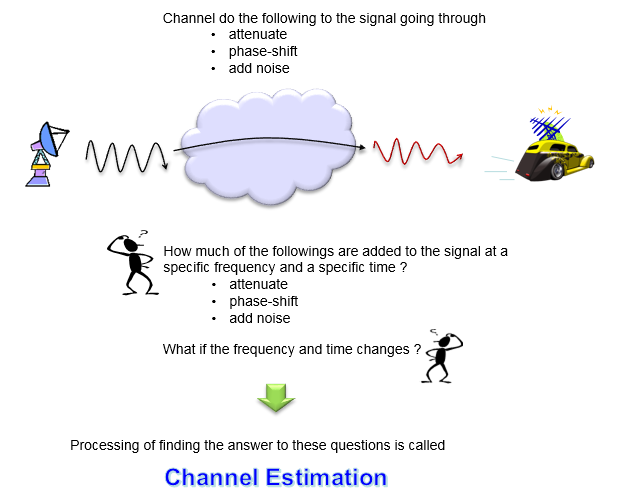
信道估计有许多不同的方法,但基本概念是相似的。过程如下所述:
- 建立一个数学模型,使用“信道”矩阵关联“发送信号”和“接收信号”。
- 发送已知信号(通常称之为“参考信号”或“导频信号”),并检测接收到的信号。
- 通过比较发送信号和接收信号,我们可以计算出信道矩阵的每个元素。
下面介绍这个过程的实现,但是由于很多细节取决于实现(这意味着详细的算法可能会随着每个特定芯片组的实现而变化),因此只能介绍整体过程。然而,总体概念是相似的。
通用算法
如何获取信道特性?如何做信道估计?整体来看,可以概括如下:
- 嵌入一组预定义的信号(称为参考信号);
- 当这些参考信号通过通道时,它会与其他信号一起失真(衰减、相移、噪声);
- 在接收处检测/解码接收到的参考信号;
- 比较发送的参考信号和接收的参考信号,并找出它们之间的相关性。
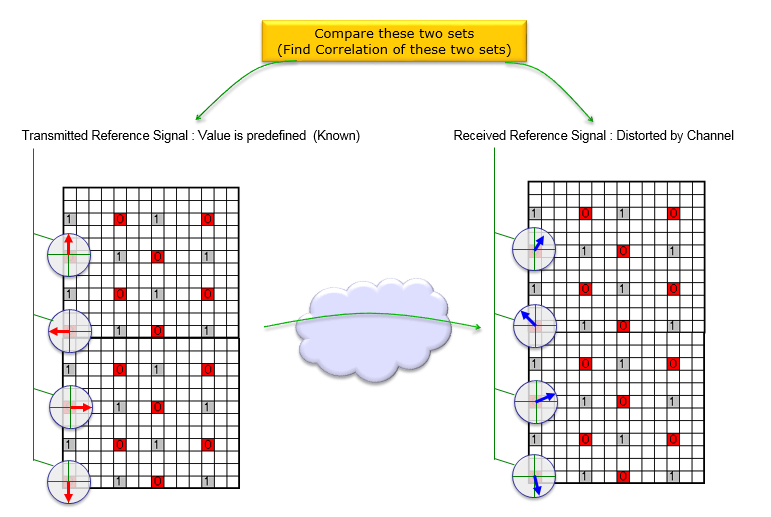
SISO场景下的信道估计
考虑LTE SISO,如何估计信道特性(信道系数和噪声估计)。
由于这是SISO,所以参考信号仅嵌入一个天线端口(端口0)。资源图中的垂直线表示频域。用 \(f_{1},f_{2},f_{3},...,f_{n}\) 表示每个参考信号。参考信号的每个符号可以是一个复数(I/Q数据),如下图所示。左侧(传输侧)的每个复数(参考符号)变为(失真)为右侧(接收符号)的每个对应符号。信道估计是在左边的复数数组和右边的复数数组之间寻找相关性的过程。
估计的详细方法可能很大程度上取决于实际情况。这里描述的方法基于开源代码:srsLTE
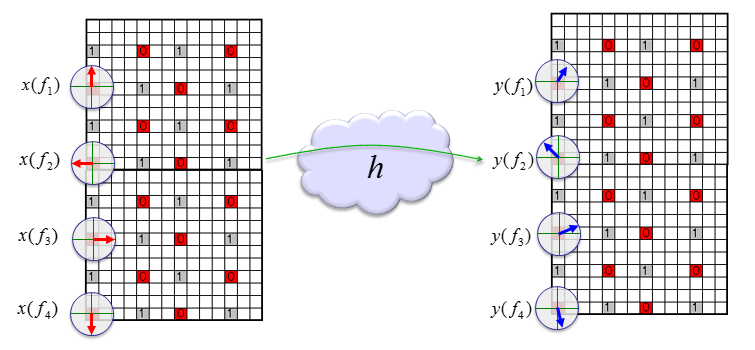
信道矩阵系数的估计
由于只有一个天线,每个发送参考信号和接收参考信号的系统模型可以表示为如下图。 \(y()\) 表示接收参考信号的数组, \(x()\) 表示发送参考信号的数组, \(h()\) 表示信道系数的数组。 \(f_{1},f_{2},f_{3},...,f_{n}\) 只是整数索引。
\(y\left(f_{1}\right)=h\left(f_{1}\right) \cdot x\left(f_{1}\right)\)
\(y\left(f_{2}\right)=h\left(f_{2}\right) \cdot x\left(f_{2}\right)\)
\(y\left(f_{3}\right)=h\left(f_{3}\right) \cdot x\left(f_{3}\right)\)
\(y\left(f_{4}\right)=h\left(f_{4}\right) \cdot x\left(f_{4}\right)\)
\(x()\) 是发送端已知的, \(y()\) 是接收端测量/检测出来的,也是已知的,这样可以计算出信道矩阵的系数,公式如下:
\(h\left(f_{1}\right)=y\left(f_{1}\right) \cdot x^{H}\left(f_{1}\right)\)
\(h\left(f_{2}\right)=y\left(f_{2}\right) \cdot x^{H}\left(f_{2}\right)\)
\(h\left(f_{3}\right)=y\left(f_{3}\right) \cdot x^{H}\left(f_{3}\right)\)
\(h\left(f_{4}\right)=y\left(f_{4}\right) \cdot x^{H}\left(f_{4}\right)\)
现在得到了参考信号所在位置所有信道矩阵的系数。
但是需要所有位置的信道矩阵系数,包括那些没有参考信号的点。
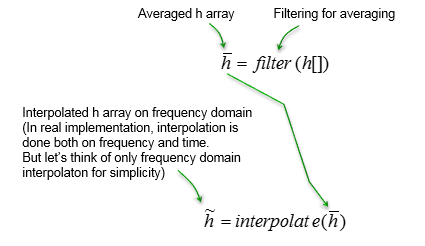
这意味着需要计算出那些没有参考信号的位置的信道系数。最常用的方法是对测量的系数数组进行插值。在srsLTE中,它首先进行平均,然后对平均信道系数进行插值。
噪声的估计
理论上,噪声可以计算如下:
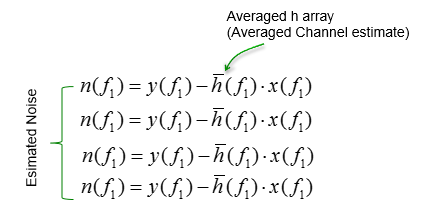
但是实际上,需要知道的是噪声的统计特性,而不是具体的值。
可以仅使用测量的信道系数和平均信道来估计噪声,如下图所示(实际上,精确的噪声值没有太大意义,因为噪声值不断变化,使用这些特定的噪声值是没有用的)。在srsLTE中,作者使用了这种方法:
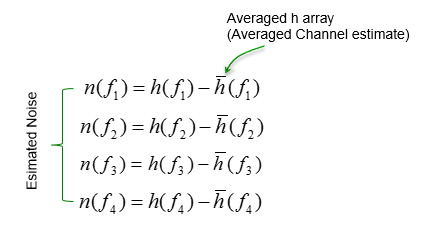
2 x 2 MIMO场景下的信道估计
假设有如下所示的通信系统。 \(x(t)\) 表示发送信号, \(y(t)\) 表示接收信号。当 \(x(t)\) 被传输到空气(信道)中时,它会失真,产生各种噪声,并可能相互干扰。因此,接收信号 \(y(t)\) 不会与发送信号 \(x(t)\) 相同。
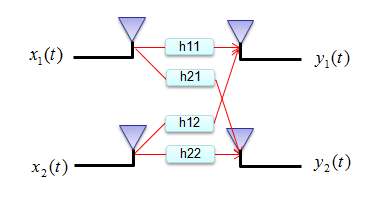
发射信号、接收信号和信道矩阵之间的这种关系可以用如下所示的数学形式建模。
\(\left[\begin{array}{l}y_{1} \\ y_{2}\end{array}\right]=\left[\begin{array}{ll}h_{11} & h_{12} \\ h_{21} & h_{22}\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]+\left[\begin{array}{l}n_{1} \\ n_{2}\end{array}\right]\)
该公式中, \(x_{1},x_{2}\) 是发送信号,已知, \(y_{1},y_{2}\) 是检测出的信号,已知。未知的是信道矩阵 \(H\) 和噪声 \(n_{1},n_{2}\) 。
为了简单起见,假设信道中没有噪声,也就是 \(n_{1},n_{2}\) 为0。(当然,在真实的信道中总是有噪声,估计噪声是信道估计的一个非常重要的部分)。
在已有数学模型的基础上,下一步是传输一个已知信号(参考信号),并从参考信号中计算出信道参数。
假设只通过一个天线发送了一个振幅为1的已知信号,而另一个天线处于关闭状态。因为信号通过空气传播,它将被接收侧的两个天线检测到。现在假设第一根天线接收到的参考信号的振幅为0.8,第二根天线接收到的参考信号的振幅为0.2。根据这个结果,我们可以算出一行信道矩阵 \(H\) ,如下所示。
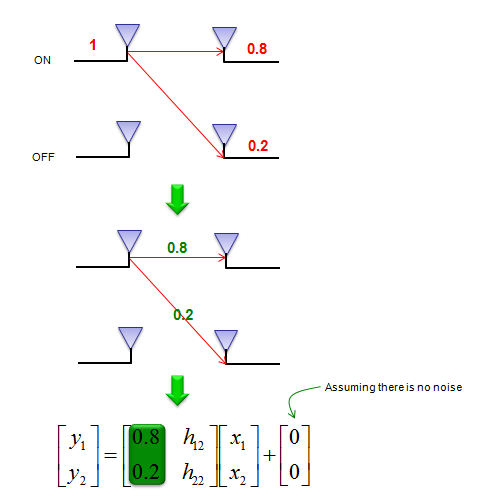
假设只通过另一个(第二个)天线发送了振幅为1的已知信号,第一个天线关闭。因为信号通过空气传播,它将被接收侧的两个天线检测到。现在假设第一根天线接收到的参考信号的振幅为0.3,第二根天线接收到的参考信号的振幅为0.7。根据这个结果,我们可以算出一行信道矩阵 \(H\) ,如下所示。
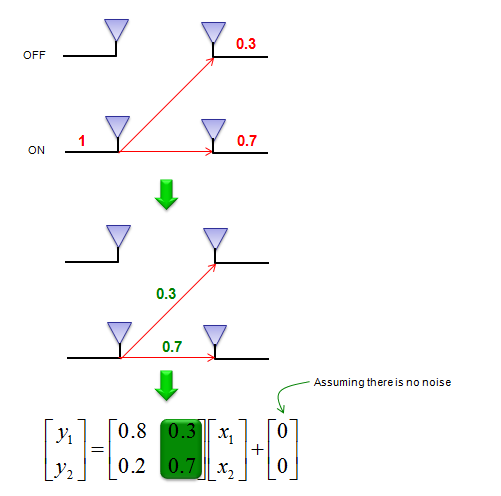
根据上面解释的概念,应该有一个时刻,仅发送参考信号而不发送实际数据,只是为了估计信道信息,这意味着由于信道估计过程,数据速率将降低。为了消除这种低效率,实际的通信系统同时传输参考信号和数据。
现在的问题是“如何在同时传输参考信号和数据的同时实现上述概念?”。有几种不同的方法可以做到这一点,不同的通信系统会使用一些不同的方法。
以LTE为例,使用如下所示的方法。在LTE中的2x2mimo的情况下,每个子帧每个天线的参考信号具有不同的位置。天线0的子帧发送了分配给天线0的参考信号,而在分配给天线1的参考信号处不发送任何信号。天线1的子帧发送了分配给天线1的参考信号,而在分配给天线0的参考信号处不发送任何信号。因此,如果你在两个接收器天线上解码为天线0的参考信号分配的RE,你可以估计 \(h_{11},h_{12}\) 。(为了简单起见,这里我们还假设没有噪音)。如果在两个接收器天线处解码为天线1的参考信号分配的资源元素,则可以估计 \(h_{21},h_{22}\) 。(为了简单起见,这里我们还假设没有噪音)。
信道系数的估计
上面说明的过程是测量LTE OFDMA符号中频域中的一个特定点的H矩阵。如果在解码符号的其他部分的过程中应用测量的H值,解码符号的精度可能不如预期的好,因为上一步中使用的测量数据将包含一定程度的噪声。因此,在实际应用中,对通过上述方法测量的 \(H\) 值进行某种后处理,在此后处理过程中,我们可以计算出噪声的总体统计特性(例如,噪声的均值、方差和统计分布)。需要记住的一点是,在这个过程中获得的特定噪声值本身并没有多大意义。从参考信号获得的特定值将与解码其他数据(非参考信号)的噪声值不同,因为噪声值随机变化。然而,这些随机噪声的总体特性可能是一个重要信息(例如,用于信噪比估计等)。
即使我们将一个包含噪声项的系统方程描述如下,但这并不意味着你可以直接测量噪声。这是不可能的。这个方程只表明检测到的信号 \(y\) 包含噪声分量的特定部分。
\(\left[\begin{array}{l}y_{1} \\ y_{2}\end{array}\right]=\left[\begin{array}{ll}h_{11} & h_{12} \\ h_{21} & h_{22}\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]+\left[\begin{array}{l}n_{1} \\ n_{2}\end{array}\right]\)
所以,测量得到信道矩阵后,改用如下公式:
\(\left[\begin{array}{l}y_{1} \\ y_{2}\end{array}\right]=\left[\begin{array}{ll}h_{11} & h_{12} \\ h_{21} & h_{22}\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]\)
在LTE的具体应用中,在一个OFDM符号内有多个测量点(多个参考信号)。这些测量点在频域上表示。那么,重写通道矩阵如下,以指示每个通道矩阵的测量点。
\(H(f)=\left[\begin{array}{ll}h(f)_{11} & h(f)_{12} \\ h(f)_{21} & h(f)_{22}\end{array}\right]\)
假设已经测量了整个OFDM符号的 \(H\) 矩阵,会有多个 \(H\) 矩阵,如下所示,每一个都表示一个特定频率的 \(H\) 矩阵。
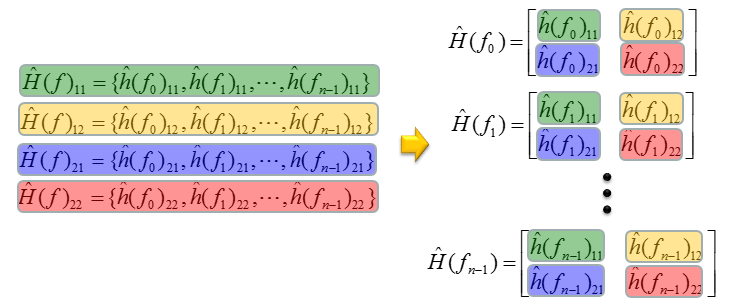
\(\begin{aligned} H\left(f_{0}\right) &=\left[\begin{array}{ll}h\left(f_{0}\right)_{11} & h\left(f_{0}\right)_{12} \\ h\left(f_{0}\right)_{21} & h\left(f_{0}\right)_{22}\end{array}\right] \\ H\left(f_{1}\right) &=\left[\begin{array}{ll}h\left(f_{1}\right)_{11} & h\left(f_{1}\right)_{12} \\ h\left(f_{1}\right)_{21} & h\left(f_{1}\right)_{22}\end{array}\right] \\ H\left(f_{n-1}\right) &=\left[\begin{array}{ll}h\left(f_{n-1}\right)_{11} & h\left(f_{n-1}\right)_{12} \\ h\left(f_{n-1}\right)_{21} & h\left(f_{n-1}\right)_{22}\end{array}\right] \end{aligned}\)
现在有一个 \(H\) 矩阵的数组。这个数组由四个不同的组组成,每个组用不同的颜色高亮显示,如下所示。
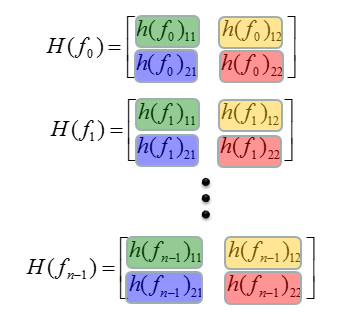
应用后处理算法时,该算法需要分别应用于这些组中的每个组。为了简单起见,将 \(H\) 矩阵的数组重新排列为多个独立数组(本例中为4个数组),如下所示。
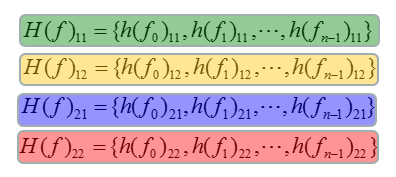
对于这些数组中的每一个,进行如下所示的相同处理。(每个芯片组制造商可能会采用稍微不同的方法,但总体思路是相似的)。在下面所示的方法中,数据(每个频点的信道系数数组)通过IFFT,这意味着dta被转换为时域,从而产生标记为(2)的时域数据数组。实际上,这是特定信道路径的脉冲响应。然后我们对这个时域数据应用特定的滤波器(或加窗)。在本例中,将某个点的数据替换为零,并创建标记为(3)的结果。您可以应用更复杂的滤波器或加窗,而不是这种简单的置零。然后,通过将滤波后的信道脉冲数据转换回频域,得到滤波后的信道系数,并在解码其他接收信号(即解码非参考数据)的过程中使用该值作为“估计信道系数”。
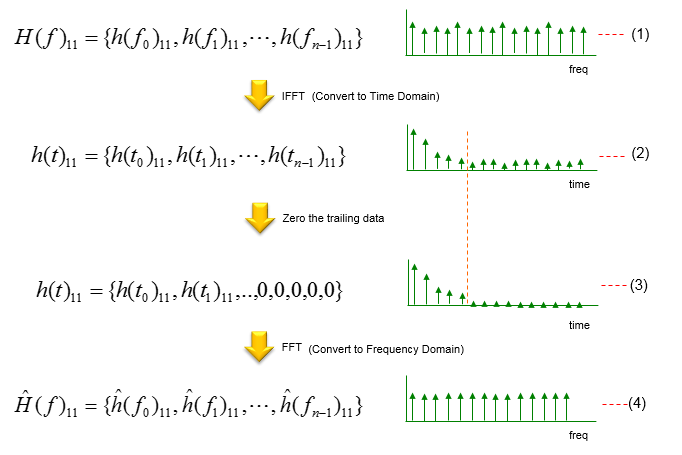
通过对所有四个数组执行相同的过程,可以得到“估计信道系数数组”的四个数组。从这四个阵列中,可以按如下方式重建估计信道矩阵的阵列。
噪声的估计
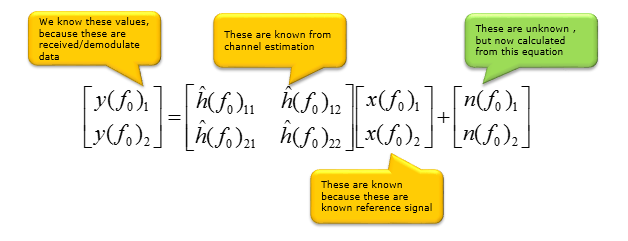
使用此估计的信道矩阵,可以使用以下等式估计每个点的噪声值。这与开始的原始系统方程相同,只是 \(H\) 矩阵被“估计 \(H'\) ”矩阵替换,现在得到了除噪声值以外的所有值。因此,通过插入所有已知值,我们可以计算(估计)每个测量点的噪声值。
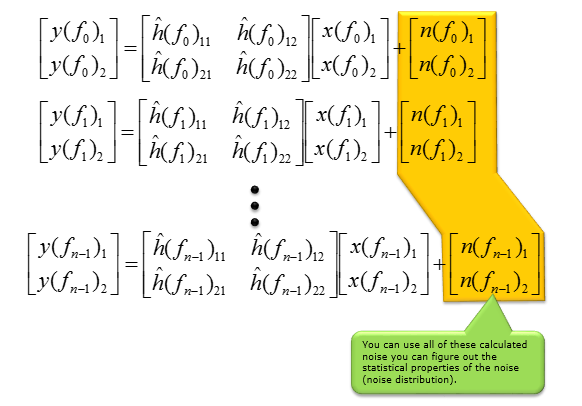
如果对所有测量点应用这个方程,会得到所有测量点的噪声值,从这些计算出的噪声值可以得到噪声的统计特性。如上所述,此处计算的每个单独噪声值没有太大意义,因为该值不能直接适用于解码其他信号(非参考信号),但这些噪声的统计特性可以是确定信道性质的非常有用的信息。
Reference :
[1] srsLTE: \srslte\lib\ch_estimation\chest_dl.c - srslte_chest_dl_estimate_port()
[2] Channel Estimation (Mathworks, LTE Toolbox)
[3] NR Synchronization Procedures

