CDD (Cyclic Delay Diversity)
本文翻译自http://www.sharetechnote.com/
CDD的概念
CDD是一种发射分集机制，通过对每个OFDM子载波应用不同的相位延迟（循环相位延迟）来实现。它用于空间多路复用，以增加两条空间路径之间的分集。
简单地说，在CDD中，一个天线正在传输数据的原始副本，另一个天线正在传输原始数据的循环移位版本，如下图所示（请参见黄色部分如何表示循环移位）：
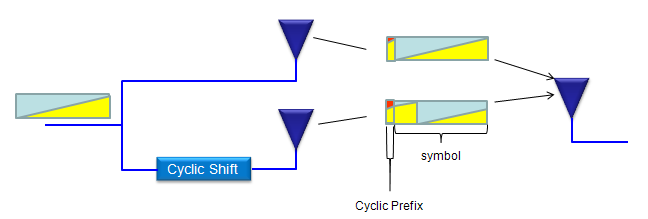
如果在频域中表示传输的数据，则原始数据和其循环移位版本见下图。时域中的循环移位为频域中的每个符号提供相移，并产生与频率分集相同的效果。
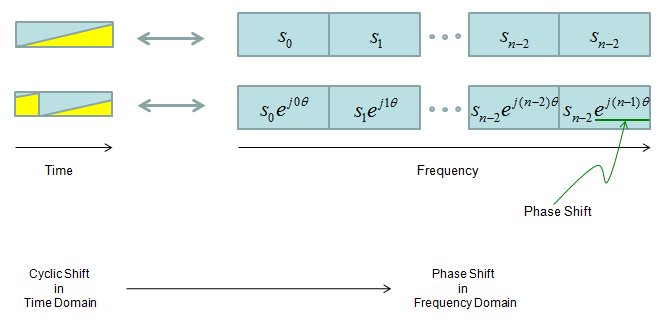
CDD在每种传输模式下的应用不同，如下表所示。
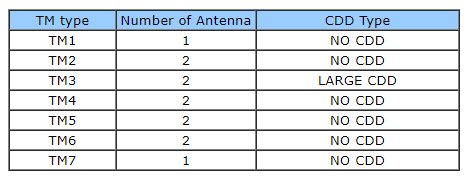
关于NO CDD和LARGE CDD的区别，参见36.211的6.3.4.2 Precoding for spatial multiplexing或者precoding section of LTE Basic Procedure page（通过公式才能理解）。
CDD的具体实现
如下图所示，CDD是通过在预编码过程中将两个附加矩阵 \(D,U\) 应用于信道矩阵 \(W\) 来实现的。在预编码步骤中应用CDD意味着CDD的真正实现是在频域中完成的，并将在通过天线发送之前转换到时域。
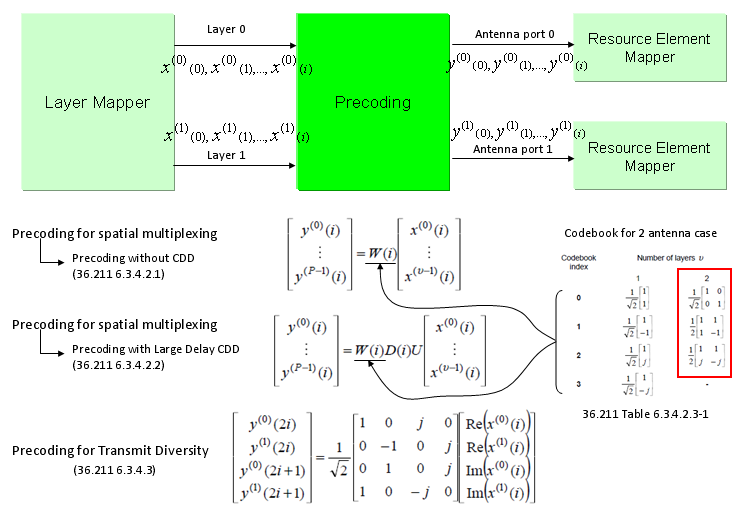
查看预编码的CDD部分，矩阵如下图所示。注意到矩阵 \(D(i)\) 是对角阵，除了对角线，它都是零值。对角线上的值实现了相移。如图中显示：预编码矩阵 \(W(i)\) 的作用是把信号分布到每个物理天线上，对角阵 \(D(i)\) 实现相移，矩阵 \(U\) 在每一层之间分配能量。
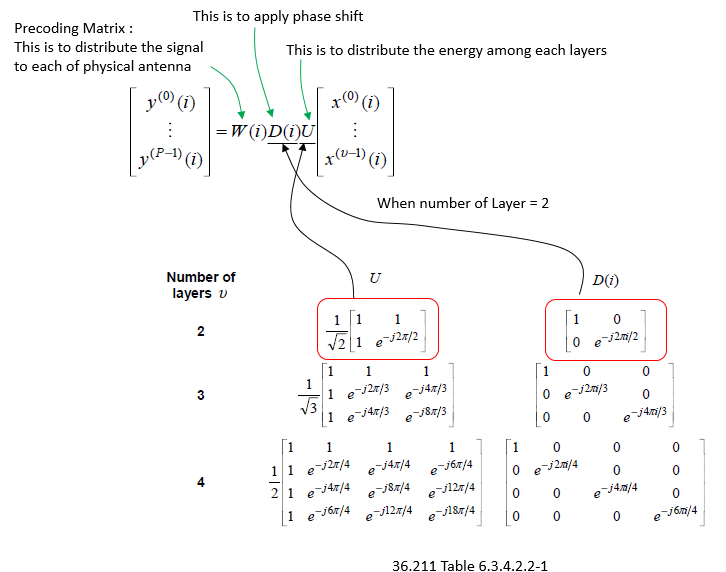
矩阵 \(D(i)\) 是对角阵，除了对角线，它都是零值。对角线上的值实现了相移，解释如下：
根据复数乘法的几何意义：复数的乘法就是平面整体旋转和伸缩，旋转量和放大缩小量恰好是这个复数对应向量的夹角和长度，并且矩阵 \(D(i)\) 中均为模为1的复数，所以 \(D(i)\) 只会影响 \(W(i)\) 的角度，不会改变幅度。
又根据矩阵乘法：矩阵 \(A\) 乘对角阵，等于对角阵的对角线元素依次和矩阵 \(A\) 每一列的所有元素相乘。所以 \(D(i)\) 的每个对角线元素分别与 \(W(i)\) 的对应列的所以元素相乘，也就是对每一列的元素都旋转对应的角度，而列与列之间的旋转角度不同。
通过观察其中的数学运算可以更好地理解其中的机制。
将2x2 CDD矩阵代入预编码公式，得到如下图中的形式。（为了简单起见，忽略其中的 \(W(i)\) 部分， \(W(i)\) 只实现缩放，没有任何相移或旋转操作）。下面试着理解矩阵 \(D(i)\) 和 \(U\) 的整体作用。并注意到 \(D(i)\) 的 \(D(2,2)\) 根据 \(i\) 的奇偶在 \(+1,-1\) 之间切换。
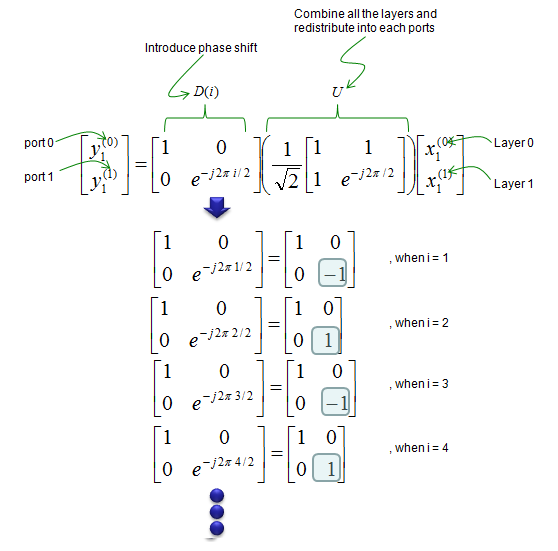
为了进一步分析，展开上图中公式如下图所示。如果将层映射的结果与CDD矩阵相乘，将会发现每个符号是如何组合并分配给每个天线的。注意，根据符号索引是奇数还是偶数，得到的结果不同。
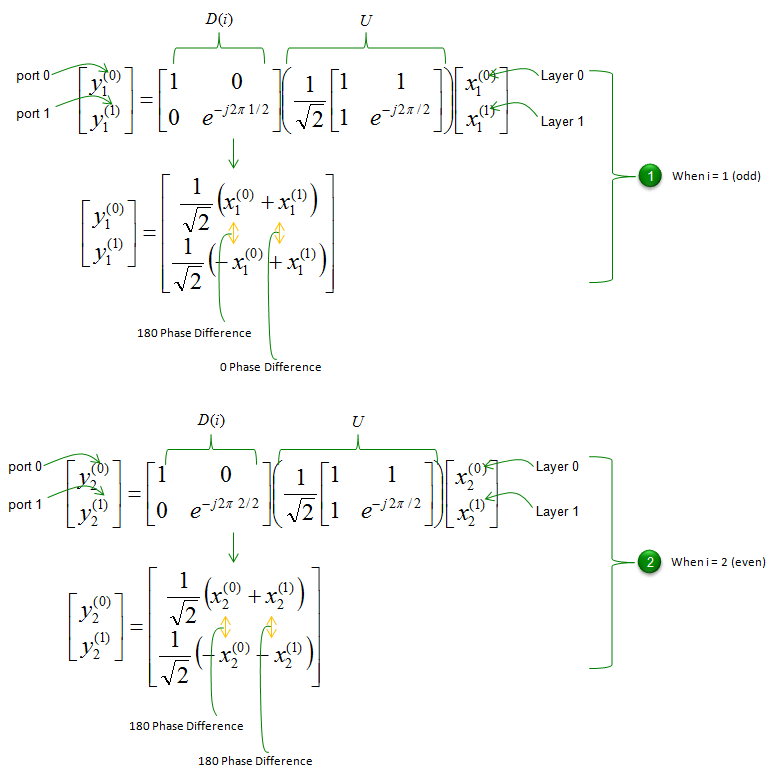
下面是一些可以从上述公式得到的事实：
- 每个天线端口（端口0和端口1）传发送来自2个layer的部分。（来自2个layer的符号线性组合，并在两个天线端口之间重新分配）
- 天线0和天线1之间的layer 1数据的相位差为180或0，具体取决于 \(i\) 。
- 天线0和天线1之间的layer 0数据的相位差为0或180，具体取决于 \(i\) 。
- 在天线端口1上，奇数符号和偶数符号之间的layer 0和layer 1上数据的相位差为180。
- 在天线端口0上，奇数符号和偶数符号之间的layer 0和layer 1上数据的相位差为0。
上述1和2表示，相同的信号（layer 0或layer 1数据）从两个Tx天线端口传输，每个子载波的相位关系以180度的步长改变。
2022-03-12 09:28:38 星期六
