SA (后缀数组) 学习笔记

今天没事干，学了SA（其实是模拟赛挂了）。

引用资料:

2009年国家集训队论文

洛谷日报273期

下面开始口胡

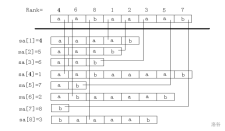
我们记 \(sa_i\) 为排名为 \(i\) 的后缀的开始位置。\(rk_i\) 为开始位置为 \(i\) 的后缀的排名。

我们采用基数排序，因为这样在排序第一关键字的时候，第二关键字顺序相对正确。（举例子就是21和12排序，因为你的程序不知道什么时候停止，如果从高到低一位一位排序，结果是 12 21,但是从低到高一位一位排序，结果是 21 12）

所以我们同时采用先排序第二关键字，再排序第一关键字。

然后就按 \(2^i\) 位直接多次基数排序。

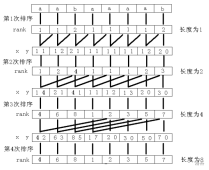
先初始化

    for (ll i = 0; i < N; i++) buc[rk[i] = ss[i]]++;
    for (ll i = 1; i <= M; i++) buc[i] += buc[i-1];
    for (ll i = N-1; i >= 0; i--) sa[--buc[rk[i]]] = i;

然后我们可以发现，对此时第二关键字排序的结果可以直接知道，那么我们只用考虑排序这次的第一关键字了。

    for (ll k = 1; k < N; k <<= 1) {
        ll num = 0;
        for (ll i = N-k; i < N; i++) y[num++] = i;
        //y[i]:记录第二关键字排序之后排第i位的对应rk[]数组的下标是谁
        for (ll i = 0; i < N; i++) if (sa[i] >= k) y[num++] = sa[i] - k;
        for (ll i = 0; i <= M; i++) buc[i] = 0;

然后直接对第一关键字排序。

        for (ll i = 0; i < N; i++) buc[rk[y[i]]]++;
        for (ll i = 1; i <= M; i++) buc[i] += buc[i-1];
        for (ll i = N-1; i >= 0; i--) sa[--buc[rk[y[i]]]] = y[i], y[i] = 0;

最后交换一下 \(rk\) 和 \(y\)（也就是把上次的 \(rk\) 放到 \(y\) 里） 然后更新 \(rk\)。

        num = 0;
        swap(rk, y);
        rk[sa[0]] = 0;
        for (ll i = 1; i < N; i++) rk[sa[i]] = (y[sa[i]] == y[sa[i-1]] && y[sa[i] + k] == y[sa[i-1] + k]) ? num : ++num;
        if (num == N) break;
        M = num;

如果 \(rk\) 已经不相同，那么可以直接break。 字符集大小如果缩小了，那么用M缩小一下（节约时空）。

#include <iostream>
#include <cstring>
#include <cstdio>

using namespace std;

typedef long long ll;
const ll MAXN = 2e6+10;

char ss[MAXN];
ll N, M = 200, buc[MAXN], rk[MAXN], y[MAXN], sa[MAXN];

void SA();

int main() {
    scanf("%s", ss);
    N = strlen(ss);
    SA();
    for (ll i = 0; i < N; i++)
        printf("%lld ", sa[i] + 1);
    return 0;
}

void SA() {
    for (ll i = 0; i < N; i++) buc[rk[i] = ss[i]]++;
    for (ll i = 1; i <= M; i++) buc[i] += buc[i-1];
    for (ll i = N-1; i >= 0; i--) sa[--buc[rk[i]]] = i;
    for (ll k = 1; k < N; k <<= 1) {
        ll num = 0;
        for (ll i = N-k; i < N; i++) y[num++] = i;
        for (ll i = 0; i < N; i++) if (sa[i] >= k) y[num++] = sa[i] - k;
        for (ll i = 0; i <= M; i++) buc[i] = 0;
        for (ll i = 0; i < N; i++) buc[rk[y[i]]]++;
        for (ll i = 1; i <= M; i++) buc[i] += buc[i-1];
        for (ll i = N-1; i >= 0; i--) sa[--buc[rk[y[i]]]] = y[i], y[i] = 0;
        num = 0;
        swap(rk, y);
        rk[sa[0]] = 0;
        for (ll i = 1; i < N; i++) rk[sa[i]] = (y[sa[i]] == y[sa[i-1]] && y[sa[i] + k] == y[sa[i-1] + k]) ? num : ++num;
        if (num == N) break;
        M = num;
    }
}