【译文】如何理解导数：乘积,幂次和链式法则

（以下大部分机翻，仅供个人兴趣学习）

我从来没有真正理解过那些乱七八糟的求导规则。加法法则，乘法法则，除法法则——它们是如何结合在一起的?

以下是我对导数的看法：

• 我们有一个系统来分析，我们的函数f
• 导数f (又名df/dx)是逐时刻行为
• 事实证明，f是一个系统的一部分(h = f+g)
• 利用部分的行为，我们能弄清楚整体的行为吗？

是的。每个部分都有一个关于它增加了多少变化的“观点”。结合每个观点以获得整体行为。每个派生规则都是合并各种观点的示例。
我们为什么不一次分析整个系统？出于同样的原因，你不会一口吃完一个汉堡包: 小部分的分解更容易理解。
与其记住单独的规则，不如让我们看看它们是如何组合在一起的：

功能：任何东西，除了图形之外的任何东西
默认的微积分解释写着“f(x) =x^2”，然后把一个图表扔到你的脸上。这真的有助于我们的理解吗？
至少不适合我。图形将输入和输出压缩为一条曲线，并隐藏将一个变成另一个的机器。 但是衍生规则是关于机器的，所以让我们看看吧！
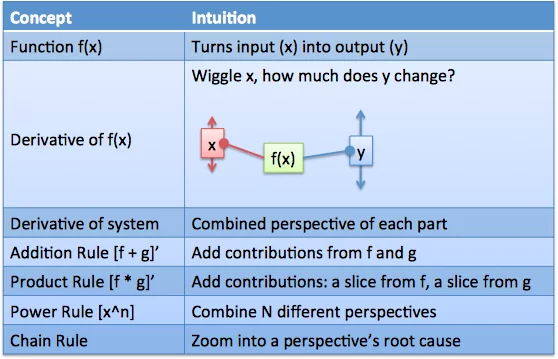
我将函数可视化为过程“input (x) => f => output (y) ”。

不仅仅是我。看看这个令人难以置信的机械目标计算机(YouTube系列的开始)。

机器用齿轮计算加法和乘法等函数一一你可以看到力学的展开！

将函数f视为具有输入杆“x”和输出杆“y”的机器。当我们调整x时，f设置y的高度。另一个类比：x是输入信号，f接收它，做一些魔术，然后吐出信号y。使用任何有助于点击的类比。

摆动

导数是函数的“逐刻”行为。那是什么意思？(不要盲目地喃喃自语“导数是斜率”。 看到这些部分周围的任何图表了吗？）
导数可以看错摆动的幅度。杠杆在x处，我们“摆动”它，看看y如何变化。“哦，我们移动了1毫米的输入杆，输出移动了5毫米，很有趣。”
结果可以写成'每个输入摆动的输出摆动”或’dy/dx”(在我们的例子中为5mm/1mm = 5) 这通常是一个公式，而不是静态值，因为它可能取决于你当前的输入。
例如，当f (x) =x^2时，导数为2x。
如果我们的输入杆在x = 10并且我们稍微摆动它(将其移动dx=0.1到10.1), 则输出应该按dy变化。结果是多少？

• 我们知道 f (x) = dy/dx = 2 * x
• 在x = 10时，“每个输入摆动的输出摆动”为=2 * 10 = 20。每移动一个输入单位，输出移动20个单位。
• 如果 dx = 0.1,则 dy = 20 * dx = 20 * .1 = 2
  事实上，10^2和(10.1)人2之间的差异约为2。导数估计了输出杆将移动多远
  (一个完美的、无限小的摆动将移动2个单位;我们移动了 2.01)

理解导数规则的关键：

• 设置您的系统
• 分别摆动系统的每个部分，查看输出移动的距离
• 合并结果

总摆动是每个部分摆动的总和。

加法和减法

我们第一个系统的时间：

当输入(x)发生变化时会发生什么？
在我的脑海中，我认为“函数h接受单个输入。它将相同的输入馈送到f和g并添加 输出杆。f和g独立摆动，甚至不知道对方！

函数f知道它会促进一些摆动(df) , g知道它会促进一些摆动(dg),而我们，徘徊的监督者，知道他们个人的每时每刻行为被添加：
dh = df + dg

再次，让我们描述每个“观点”：

• 整个系统有行为dh
• 从f的角度来看，它对整体贡献了df（没有g）
• 从g的角度来看，它为整体贡献了dg（没有f）
  系统的每一次更改都是由于某些部件的变化(f和g) 如果我们将每个可能变量的贡献相加，我们就描述了整个系统。

df vs df/dx

有时我们使用df,有时使用df/dx(这让我困惑了一段时间)

• df是“无论f变化多少”的一般概念
• df/dx是一个具体的概念，即“无论f变化多少，x变化多少”

通用的“df”帮助我们查看整体行为。

打个比方：假设您正在越野驾驶，想要测量汽车的燃油效率。您将测量行驶的距离，检查您的油箱以查看您使用了多少汽油，最后进行除法以计算“每加仑英里数”。你分别测量距离和汽油，你没有跳进油箱来获得移动速率！

在微积分中，有时我们要考虑实际的变化，而不是比率。在“dnf级别工作让我们有空间思考函数的整体摆动方式。我们最终可以根据特定输入将其缩小。

我们现在就这样做。上面的加法规则可以写成，在“每dx”的基础上，如下：

\[\frac{d h}{d x}=\frac{d f}{d x}+\frac{d g}{d x} \]

乘法规则

下一个难题：假设我们的系统将部分“f”和“g”相乘。它的行为如何？

\[h(x)=f(x)\cdot g(x) \]

嗯，棘手-这些部分的相互作用更紧密。但策略是相同的：从自己的角度查看每个部分如何做出贡献，并将它们组合在一起：
看看这张图:

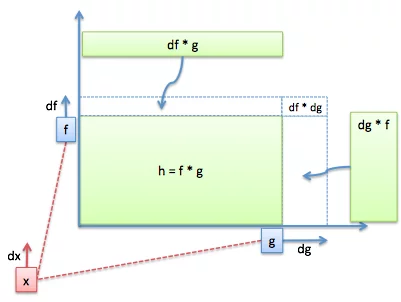
这是怎么回事？

• 我们有我们的系统：f和g相乘，得到h (矩形的面积)
• 输入“x”在远处由dx关闭。f变化一定量df (考虑绝对变化，而不是速率！同样，g会根据其自身的量dg而变化。因为f和g发生了变化，所以矩形的面积也发生了变化)。
• 从f的角度来看，面积变化是什么？好吧，f知道他被df改变了，但不知道g 发生了什么。从f的角度来看，他是唯一一个移动并会添加一片 面积=df*g
• 同样，g不知道f是如何变化的，但知道他会添加为区域切片“dg"，
• 系统的整体变化(dh)是两个区域切片：

\[d h=f\cdot d g+g\cdot d f \]

现在，就像我们的每加仑英里数示例一样，我们“除以dx”来写出x的变化量：

\[\frac{d h}{d x}=f\cdot\frac{d g}{d x}+g\cdot\frac{d f}{d x} \]

(旁白：除以dx?工程师会点头，数学家会皱眉。从技术上讲，df/dx不是一小部分：它是取导数的整个操作(有极限等等)。但从无穷小的角度来看，在直觉上，我们正在“按dx缩放"。)
乘积法则的关键是:添加两条“面积条”，每个角度各一条。

陷阱：但是f和g同时变化(df * dg)不是有一些影响吗？

是的。然而，这个区域是一个无穷小*无穷小(“二阶无穷小”)，在当前水平上是 不可见的。这是一个比较麻烦的概念，但是(df * dg) / dx与df/dx等正常导数相比 消失了。我们单独改变f和g并组合结果，而忽略它们一起移动的结果。

链式法则：没那么糟糕

假设 g 依赖于 f，而 f 依赖于 x：

\[y=g(f(x)) \]

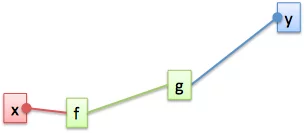
链式法则允许我们“放大”一个函数，并查看初始更改（x）如何影响最终结果(g)。

解释1：转换比率

一种常见的解释是将比率相乘：

\[\frac{d g}{d x}=\frac{d g}{d f}\cdot\frac{d f}{d x} \]

x摆动f.这会产生df/dx的变化率，该变化率按dg/df摆动g,然后，整个摆动是：

\[{\frac{d g}{d f}}\cdot{\frac{d f}{d x}} \]

这类似于化学课上的“因子标签”方法：

\[{\frac{m i l e s}{s e c o n d}}={\frac{m i l e s}{h o u r}}\cdot{\frac{1\;h o u r}{60\ m i n u t e s}}\cdot{\frac{1\;m i n u t e}{60\ s e c o n d s}}={\frac{m i l e s}{h o u r}}\cdot{\frac{1}{3600}} \]

如果你的“英里/秒”速率发生变化，乘以转换系数得到新的“英里/小时”。秒不直接知道小时——它通过秒=>分钟的转换
同样，g不直接知道x,只知道f。函数g知道它应该按dg/df缩放其输入以获得输出。初始速率(df/dx)在链上移动时被修改。

解释2：转换摆动

我更喜欢在“每次摆动”的基础上看到链式规则：

• x 摆动由dx, 所以
• 摆动由df,所以
• 摆动由dg
  但它们实际上有什么关系呢？哦，是的，导数！(这是每个输入摆动的输出摆动)：

\[d f=d x\cdot{\frac{d f}{d x}} \]

请记住，f (df/dx)的导数是缩放初始摆动的程度。同样的情况也发生在g上：

\[d g=d f\cdot{\frac{d g}{d f}} \]

它将按dg/df缩放其输入杆(f)上出现的任何摆动。如果我们用dx来写df摆动：

\[d g\equiv\left(d x\cdot\frac{d f}{d x}\right)\cdot\frac{d g}{d f} \]

我们有另一个版本的链规则：dx启动链，这会产生一些最终结果dg。如果我们想 要dx的最终摆动，请将两边除以dx：

\[\frac{d g}{d x}=\frac{d f}{d x}\cdot\frac{d g}{d f} \]

链式法则不仅仅是因子标签单位消去——它是摆动的传播，每一步都要调整。
链式法则适用于多个变量(a依赖于b依赖于c)，只要随着你的移动传播波动。
试着想象“放大”到不同变量的视角。从dx开始向上看，你会看到在脉冲到达g之前需要的整个变换链

链式法则:时间的例子

假设我们把“平方机”放在“立方机”前面:
输入(x) => f:x^2 => g:f^3 =>输出(y)
F:x^{2表示输入F的平方。g:f}3表示g对其输入f的值进行立方。例如:
输入(2)=> f(2) => g(4) =>输出:64
从2开始，f对它平方(2^2 = 4)g对它立方(4^3 = 64)这是第六动力机器

\[g(f(x))=(x^{2})^{3} \]

它的导数是什么?

\[{\frac{d g}{d x}}={\frac{d g}{d f}}\cdot{\frac{d f}{d x}} \]

• f改变了它的输入波动df/dx = 2x
• g改变了它的输入波动dg/df = 3f^2
  最后一个变化是:

\[3f^{2}\cdot2x=3(x^{2})^{2}\cdot2x=3x^{4}\cdot2x=6x^{5} \]

链式法则:陷阱

函数将它们的输入视为一团

在这个例子中，g的导数(“x^3 = 3x^{2”)并不是指原来的“x”，而是指输入的任何东西(foo}3 = 3*foo^2)。输入是f，它把f当作一个单独的值。之后，我们匆忙地把f写成x的形式，但是g与此无关——它不关心f是否可以写成更小的形式。

在许多例子中，变量“x”是“行尾”。

题目问的是df/dx。"从x的角度给我一些改变"现在，x可以依赖于更深层次的变量，但这不是要求。这就像在说“我想要每小时英里数。我不关心英里每分钟或英里每秒。只要给我每小时几英里就行了。”Df /dx的意思是，一旦得到x，就不要再看输入了。

为什么我们用链式法则乘导数，而把其他的加起来呢?

常规的规则是关于结合观点来获得一个整体的画面。我看到了什么变化?g看到了什么变化?把它们加起来就是总数。

链式法则是深入到单个部分(比如f)看它是否受另一个变量控制。这就像看着时钟内部说:“嘿，分针是由秒针控制的!”我们待在同一个地方。

当然，最终f的“每秒”视角可以添加到g的某些视角中。但链式法则是关于深入挖掘“f”的根本原因。

幂法则:经常被记住，很少被理解

x^4的导数是什么?4 x ^ 3 ?太好了。把指数拿下来减1。现在解释一下为什么!

有几种方法，但这里是我最喜欢的:x^4实际上是x * x * x * x，它是4个“独立”变量的乘法。每个x都不知道其他x的存在，就像x * u * v * w一样。

现在考虑第一个x的角度

• 它从x变成x + dx
• 整个函数的变化是[(x + dx) - x][u * v * w] = dx[u * v * w]
• 以“每dx”为基础的变化是[u * v * w]

同样的,

• 从u的角度来看，它改变了du。它在“每dx”的基础上贡献(du/dx)*[x * v * w]
• V贡献(dv/dx) * [x * u * w]
• W贡献(dw/dx) * [x * u * v]

谜底揭开了:x、u、v和w是一样的!“视点”转换因子为1 (du/dx = dv/dx = dw/dx = dx/dx = 1)，总变化量是：

\[(x\cdot x\cdot x)+(x\cdot x\cdot x)+(x\cdot x\cdot x)+(x\cdot x\cdot x)=4x^{3} \]

喘口气

我希望你们能从新的角度来看待导数:我们有一个由部分组成的系统，我们摆动输入，看看整个系统是如何运动的。它是关于结合观点:每个部分对整体有什么贡献？
在后续文章中，我们将看到更强大的规则(指数、商数等)。快乐数学。

原文地址