谈一谈特征选择(一)

前言：本系列博客将介绍特征选择一系列相关的内容。

本节我们先简介特征工程中的三个组成部分。

---

特征工程

特征工程一般由特征构建，特征提取，特征选择三个部分组成。
特征工程的思维导图如下：

来源

先约定一些符号:

设\(D\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}\)是一个含有\(n\)个样本\(m\)个特征的数据集。
其中\(x_i\)为样本，\(y_i\in \{1,2,...,d\}\)为样本\(x_i\)的标签。\(C=\{c_1,c_2,...,c_m\}\)是\(m\)个特征的集合。
\(x_{ij}(1\leq i\leq n,1 \leq j \leq m)\)表示第\(i\)个样本的第\(j\)个特征上的值。
\(|\cdot|\)表示集合含有元素的个数，当\(c_j\)为离散特征时，\(c_j\)的取值集合\(C_j\)为\(\{c_{j1},c_{j2},...,c_{jk},...,c_{j|c_j|}\},(1 \leq j \leq m,1 \leq k \leq |c_j|)\)，\(|c_j|\)为特征\(c_j\)含元素个数。

对于某一个特征\(c_j\)，有\(\forall i,x_{ij} \in \{c_{j1},c_{j2},...,c_{jk},...,c_{j|c_j|}\}\)。

样本空间构成的矩阵如下：

\[\left(\begin{array}{ccccccc} {x_{11}} & {x_{12}} & {\cdots} & {x_{1 j}} & {\cdots} & {x_{1 m}} & {y_{1}} \\ {x_{21}} & {x_{2}} & {\cdots} & {x_{2 j}} & {\cdots} & {x_{2 m}} & {y_{2}} \\ {\vdots} & {\vdots} & {} & {\vdots} & {} & {\vdots} & {\vdots} \\ {x_{11}} & {x_{i 2}} & {\cdots} & {x_{i j}} & {\cdots} & {x_{i m}} & {y_{i}} \\ {\vdots} & {\vdots} & & {\vdots} & & {\vdots} & {\vdots} \\ {x_{n 1}} & {x_{n 2}} & {\cdots} & {x_{n j}} & {\cdots} & {x_{n m}} & {y_{n}} \end{array}\right) \]

特征构建

特征构建是指从原始特征中推断或构建出新的特征。

在我们的原始样本空间中，\(C=\{c_1,c_2,...,c_m\}\)有\(m\)个特征，通过特征构建，从原始\(m\)个特征中推断或者构建出了\(l\)个新特征，新的样本空间特征集为\(C=\{c_1,c_2,...,c_m,c_{m+1},...,c_{m+l}\}\)，有了\(m+l\)个特征了。

我们先看一个简单的例子，就以学生成绩来看吧。

学号	语文	数学	英语	物理	化学	生物
001	90	120	130	100	80	70
002	70	110	110	60	60	60
003	50	40	120	90	80	80
004	40	60	100	70	60	60
005	130	90	90	80	80	80
006	70	50	90	60	60	60
007	90	70	140	50	50	50
008	20	140	100	90	70	50
009	120	130	80	60	60	60
010	110	90	60	50	70	60
011	100	70	50	90	90	60
012	30	100	50	80	80	60

这是一个常见的学生成绩表，有着最基本的信息。但是我们知道，在实际老师发给我们的成绩表里面内，有着各种各样的数据，相信学生时代的大家应该深有体会。

就举些常见的“参数”吧，统计各分数段人数，学生总分排名，单科成绩排名，理综排名，每科进步幅度排名等等。这些参数或者说特征都是在原有表的基础上构建的，有的是一个特征演变来的，有的是由若干个特征构建的。

特征构建的常用方法有属性分割与属性组合。属性分割就是将一个属性分解或者切分，例如学生成绩表中统计各分数段人数。属性组合就是多个属性通过组合构建出新的属性，例如理综成绩排名。

从这里可以看出特征构建是一个升维的过程，即原始样本空间的维度增加了。

特征提取

和特征构建不同的是，特征提取和特征选择都是数据降维。

数据降维主要考虑数据的相关度和数据的冗余度。
数据的相关度是指数据所包含的信息对判断样本所属类别的贡献度，而数据的冗余度指的是不同维数的数据携带的相似信息。具有高相关度的数据特征一定程度上是冗余的，会造成分类性能的恶化。我们的目标是得到一个具有最大相关性和最小冗余度的数据特征信息的样本。
数据降维都会使原有样本空间由\(m\)个特征变为\(l(l \leq m)\)个特征。

特征提取将原始特征转换为新的具有明显物理意义或者统计意义或核的特征的过程，它把原始空间的样本通过线性或者非线性映射转化得到少量但具有更好表达能力的新特征，从而达到降维的目的。

还是以上面学生成绩为例，如果我们只想使用少量的指标就能知道学生成绩的所有信息，那么我们可以使用学生各科的成绩之和等少数几个指标来代表所有的学生成绩信息。
该过程可以视为特征提取。

特征提取的主要方法有

• PCA 主成分分析，它是利用正交变换来对一系列可能相关的变量的观测值进行线性变换，从而投影为一系列线性不相关变量的值，这些不相关变量称为主成分。
• LDA 线性判别分析，它是试图找到两类事件的特征的一个线性组合，以能够特征化或区分它们，所得的组合可用来作为一个线性分类器。
• LCA 独立成分分析，它是一个线性变换。这个变换把数据或信号分离成统计独立的非高斯的信号源的线性组合。

特征选择

特征选择是在保持数据原样本的基础上进行约减，即降低特征维数。特征选择就是为了筛选出那些对于分类来说最相关的特征，并且去除那些对于分类冗余的和不相关的特征。其实质是寻求一个原始数据样本空间的最优字空间，其中包含最少的样本特征数目并且能够将原始的样本很好地表达出来，是一个降维的过程。

以西瓜数据集为例

色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
青绿	蜷缩	浊响	清晰	凹陷	硬滑	0.697	0.46	是
乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	0.774	0.376	是
乌黑	蜷缩	浊响	清晰	凹陷	硬滑	0.634	0.264	是
青绿	蜷缩	沉闷	清晰	凹陷	硬滑	0.608	0.318	是
浅白	蜷缩	浊响	清晰	凹陷	硬滑	0.556	0.215	是
青绿	稍蜷	浊响	清晰	稍凹	软粘	0.403	0.237	是
乌黑	稍蜷	浊响	稍糊	稍凹	软粘	0.481	0.149	是
乌黑	稍蜷	浊响	清晰	稍凹	硬滑	0.437	0.211	是
乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	0.666	0.091	否
青绿	硬挺	清脆	清晰	平坦	软粘	0.243	0.267	否
浅白	硬挺	清脆	模糊	平坦	硬滑	0.245	0.057	否
浅白	蜷缩	浊响	模糊	平坦	软粘	0.343	0.099	否
青绿	稍蜷	浊响	稍糊	凹陷	硬滑	0.639	0.161	否
浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	0.657	0.198	否
乌黑	稍蜷	浊响	清晰	稍凹	软粘	0.36	0.37	否
浅白	蜷缩	浊响	模糊	平坦	硬滑	0.593	0.042	否
青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	0.719	0.103	否

在一系列特征中，我们需要找到那些影响西瓜好坏与否的主要特征，而这只有特征选择才可以做到。这里面有很多的方法，之后会说到。

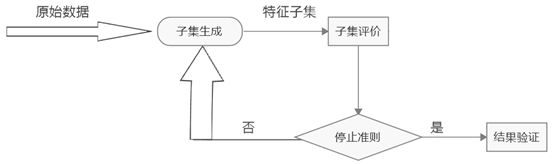
特征选择的流程如下：

1.子集生成：按照一定的搜索策略查找候选特征子集

2.子集评价：构建评价函数评估特征子集的优劣

3.停止准则：设定评估函数的阈值，决定特征选择算法什么时候停止

4.结果验证：在测试集上验证最终所选特征子集的有效性

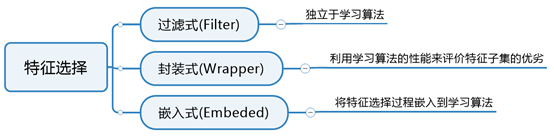
根据于学习算法的关系，特征选择可划分为三类方式：过滤时(Filter)方式，封装式(Wrapper)方法和嵌入式(Embedded)方法。

小结

本节我们简单介绍了特征工程中的三个部分，特征构建，特征提取，特征选择，之后我们将重点介绍特征选择。