特征与特征距离度量

在本节，我们将介绍什么是特征，特征的分类以及常见的特征距离度量和它们的简单实现。

什么是特征

在机器学习和模式识别中，特征是被观测对象的可测量性能或特性。在模式识别，分类和回归中，信息特征的选择，判别和独立特征的选择是有效算法的关键步骤。特征通常是数值型的，但语法模式识别可以使用结构特征(如字符串和图)。“特征”的概念与线性回归等统计技术中使用的解释变量有关。
以上内容来自于维基百科。

关于特征，特征工程这块内容很广泛，在业界广泛流传这么一句话：数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。
这里，我们也不会对特征做太多学术上的叙述，只是结合例子对特征做一些简单的描述。

特征，可以认为是描述事物的一个特性。比如说我们描述一个人，可以使用的特征很多，身高，体重，性别等等，这些特征往往都会有相应的值，身高(180 cm)，体重(70 kg)，性别(男，女)。这些特征描述了一个人的基本特性，通过身高，体重，我们想象一个人大致的轮廓。比如简历或者病历，HR可以通过简历上的内容，了解到你的经历，例如学历，实习经历，年龄等等。同样地，医生可以通过病历上面的各项指标和参数，知道你身体的大致情况，从而做出大致的判断了。

那么在机器学习里面呢，我们都会接触各种各样的数据集，不妨以西瓜数据集为例吧。

色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
青绿	蜷缩	浊响	清晰	凹陷	硬滑	0.697	0.46	是
乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	0.774	0.376	是
乌黑	蜷缩	浊响	清晰	凹陷	硬滑	0.634	0.264	是
青绿	蜷缩	沉闷	清晰	凹陷	硬滑	0.608	0.318	是
浅白	蜷缩	浊响	清晰	凹陷	硬滑	0.556	0.215	是
青绿	稍蜷	浊响	清晰	稍凹	软粘	0.403	0.237	是
乌黑	稍蜷	浊响	稍糊	稍凹	软粘	0.481	0.149	是
乌黑	稍蜷	浊响	清晰	稍凹	硬滑	0.437	0.211	是
乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	0.666	0.091	否
青绿	硬挺	清脆	清晰	平坦	软粘	0.243	0.267	否
浅白	硬挺	清脆	模糊	平坦	硬滑	0.245	0.057	否
浅白	蜷缩	浊响	模糊	平坦	软粘	0.343	0.099	否
青绿	稍蜷	浊响	稍糊	凹陷	硬滑	0.639	0.161	否
浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	0.657	0.198	否
乌黑	稍蜷	浊响	清晰	稍凹	软粘	0.36	0.37	否
浅白	蜷缩	浊响	模糊	平坦	硬滑	0.593	0.042	否
青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	0.719	0.103	否

在这个csv数据集的第一行(除了第一个)，都可以看作是一个个特征，那最后一个往往就是标签了，比如色泽就是西瓜的一个特征，色泽就会有相应的特征值，如青绿，乌黑，浅白，对于密度这个特征呢，它的取值就是连续的浮点数了。这些特征都可以描述西瓜的一部分，而好瓜作为标签，决定了瓜的种类，它的取值便是好坏与否了。

接下来我们将介绍特征的分类。

特征的分类

在简单认识了特征后，我们就可以对特征分类了，从上面的西瓜数据集可以看出，每个特征都有相应的取值，描述西瓜的一部分。而是不同特征还是有一些区别的，比如色泽和密度，区别很明显，而有些区别，却不明显，如敲声，虽然它和密度不一样，但是我们还是可以感觉出一种“程度”，混响和沉闷之间还是有“程度”上的区别的，尽管它不如密度那样直观。

现在，我们对特征做个简单的分类吧，这里我们对特征和属性不作区分，即两者的代表意思相同。

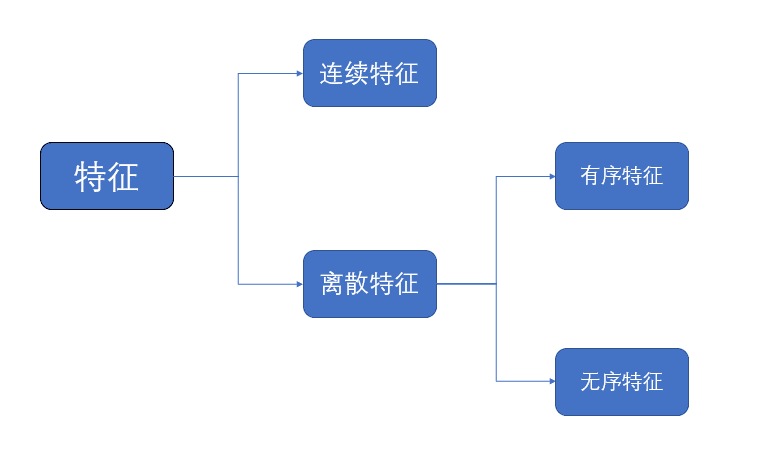
通常，我们可以将特征划分为"连续特征"和"离散特征"。
“连续特征”在定义域上有无穷多个可能的取值，比如说密度这个特征，它有无穷多个取值；而“离散特征”在定义域上是有限个取值，比如性别，只有男女之分，调查问卷中的等级之分等等。

但是呢，在距离度量时，特征上“序”的概念，或者说“程度”也是很重要的。在连续特征上，不同特征值的大小关系是很明显的，密度值的不同带来的序的关系显而易见，对于离散特征，尽管它的取值是有限个，但是序的概念依然存在。

例如，调查问卷中常见的评分标准，{"差"，"较差"，"一般"，"较好"，"好"}的离散属性与连续属性更接近一些，我们能明显感知出"好"，"较好"的距离比"好"，"一般"更近一些。这样的特征称为“有序特征”；而诸如颜色(不考虑不同颜色对应的值)，交通方式这样的特征，它们的定义域也是有限的，如交通方式{"飞机"，"火车"，"轮船"，"汽车"}，它们没有明显的序的概念，称为“无序特征”。

至此，我们可以对特征简单地分类：
特征的分类

## 特征距离度量以及实现对于函数$dist(.,.)$，我们首先看看距离度量需要满足的一些基本性质： * 非负性：$dist(x_{i},x_{j}) \geq 0$ * 同一性：$dist(x_{i},x_{j}) = 0$ 当且仅当 $x_{i} = x_{j}$ * 对称性：$dist(x_{i},x_{j}) = dist(x_{j},x_{i})$ * 传递性：$dist(x_{i},x_{j}) \leq dist(x_{i},x_{k})+dist(x_{k},x_{j})$

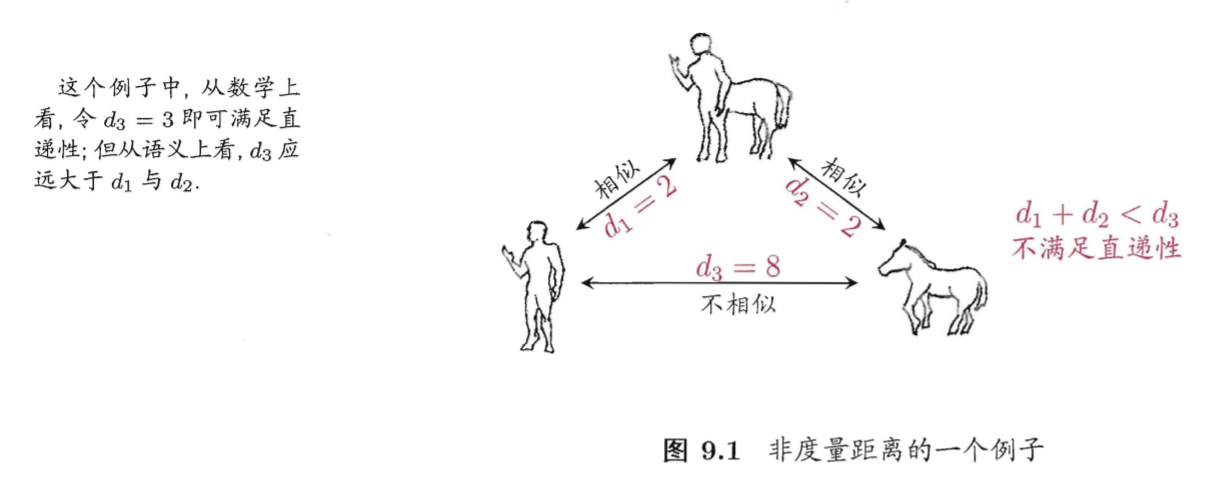
需注意的是，通常我们是基于某种形式的距离来定义"相似度度量"，距离越大，相似度越小。然而，用于相似度度量的距离未必定要满足距离度的所有基本性质，尤其是直递性。例如在某些任务中我们可能希望有这样的相似度度量："人"，"马"分别与"人马"相似，但"人"与"马"很不相似；要达到这个目的，可以令 "人"，"马"与"人马"之间的距离都比较小但"人"与"马"之间的距离很大，此时该距离不再满足直递性；这样的距离称为"非度量距离"。

如图：

接下来，我们将介绍常见的特征距离度量，第一个是针对无序特征的，其他的是针对连续特征和离散特征中的有序特征的度量方式。

在介绍连续特征和离散特征中的有序特征的度量方式前，我们先简单约定一些符号。

\[x_{i}=(x_{i1},x_{i2},...,x_{in}) \quad x_{j}=(x_{j1},x_{j2},...,x_{jn}) \]

$x_{i},x_{j}$都是$n$维空间上的向量。
$dist(x_{i},x_{j})$表示$x_{i}$和$x_{j}$之间的距离。
使用matlab实现部分度量方式。

VDW

对无序属性可采用 VDM (Value Difference Metric)。令$m_{u,a}$表示在属性$u$上取值为$a$的样本数，$m_{u,a,i}$表示在第$i$个样本簇中在属性$u$上取值为$a$的样本数，$k$为样本簇数，则属性$u$上两个离散值$a$与$b$之间的 VDM 距离为：

\[VDM_{p}(a,b)=\sum_{i=1}^{k}|\frac{m_{u,a,i}}{m_{u,a}} - \frac{m_{u,b,i}}{m_{u,b}}|^{p} \]

欧式距离

这个是我们从小到大接触的最多的距离了，其公式为：

\[dist(x_{i},x_{j})= \sqrt {\sum_{k=1}^{n}(x_{ik}-x_{jk})} \]

matlab程序：

xi = [1,2,3,4,5];
xj = [5,4,3,2,1];
dist = pdist2(xi,xj,'euclidean')
% dist = 6.3246

标准化欧氏距离

标准化欧氏距离是针对欧氏距离的缺点而作的一种改进。标准欧氏距离将各个分量都“标准化”到均值、方差相等。
假设样本集X的均值为$m$，标准差为$s$，$X$的“标准化变量”表示为：

\[X^{*}=\frac{X-m}{s} \]

标准化欧氏距离公式：

\[dist(x_{i},x_{j})=\sqrt{\sum_{k=1}^{n}(\frac{x_{ik}-x_{jk}}{s_{k}})^2} \]

matlab程序：

xi = [1,2,3,4,5];
xj = [5,4,3,2,1];
X = [xi;xj]';
xi_std = std(xi);
xj_std = std(xj);
dist = pdist(X,'seuclidean',[xi_std,xj_std])
% dist = 0.8944 1.7889 2.6833 3.5777 0.8944 1.7889 2.6833 0.8944 1.7889 0.8944

切比雪夫距离

切比雪夫距离为某一维度上的最大距离，其公式如下：

\[dist(x_{i},x_{j})=\max_{k}(|x_{ik}-x_{jk}|) \]

matlab程序：

xi = [1,2,3,4,5];
xj = [5,4,3,2,1];
dist = pdist2(xi,xj,'chebychev')
% dist = 4

曼哈顿距离

曼哈顿距离也被称为“计程车距离”，或者说“城市街区距离”，它不是走两点之间的直线，而是类似于的街道这样的线段，其公式如下：

\[dist(x_{i},x_{j})=\sum_{k=1}^{n}|x_{ik}-x_{jk}| \]

matlab程序：

xi = [1,2,3,4,5];
xj = [5,4,3,2,1];
dist = pdist2(xi,xj,'cityblock')
% dist = 12

闵可夫斯基距离

闵可夫斯基距离是一组距离的定义，是对多个距离度量公式概括性的表述，其公式为：

\[dist(x_{i},x_{j})=\sqrt[p]{\sum_{k=1}^{n}|x_{ik}-x_{jk}|^{p}} \]

当 $p=1$，为哈曼顿距离：

\[dist(x_{i},x_{j})=\sum_{k=1}^{n}|x_{ik}-x_{jk}| \]

当 $p=2$，为欧氏距离：

\[dist(x_{i},x_{j})= \sqrt {\sum_{k=1}^{n}(x_{ik}-x_{jk})} \]

当 $p=\infty$，为切比雪夫距离：

\[dist(x_{i},x_{j})=\max_{k}(|x_{ik}-x_{jk}|) \]

matlab程序如下：

xi = [1,2,3,4,5];
xj = [5,4,3,2,1];
p = 1;
% 哈曼顿距离
dist = pdist2(xi,xj,'minkowski',p)
% dist = 12
p = 2;
% 欧氏距离
dist = pdist2(xi,xj,'minkowski',p)
% dist = 6.3246
p = inf;
% 切比雪夫距离
dist = pdist2(xi,xj,'minkowski',p)
% dist = 4

马氏距离

马氏距离是基于样本分布的一种距离，其定义如下：
有$m$个样本向量$x_{1}~x_{m}$，协方差矩阵为$S$，均值记为向量$\mu$，其中样本向量$x$到$\mu$的马氏距离为：

\[dist(x,\mu)=\sqrt{(x-\mu)^{T}S^{-1}(x-\mu)} \]

向量$x_{i}$与$x_{j}$的马氏距离为：

\[dist(x_{i},x_{j})=\sqrt{(x_{i}-x_{j})^{T}S^{-1}(x_{i}-x_{j})} \]

若协方差矩阵是单位矩阵(各个样本向量之间独立同分布)，则$x_{i}$与$x_{j}$之间的马氏距离等于他们的欧氏距离：

\[dist(x_{i},x_{j})=\sqrt{(x_{i}-x_{j})^{T}(x_{i}-x_{j})} \]

若协方差矩阵是对角矩阵，则就是标准化欧氏距离:

\[dist(x_{i},x_{j})=\sqrt{\sum_{k=1}^{n}(\frac{x_{ik}-x_{jk}}{s_{k}})^2} \]

特点：

量纲无关，排除变量之间的相关性的干扰；
马氏距离的计算是建立在总体样本的基础上的，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；
计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离计算即可。

matlab程序如下：

xi = [1,2,3,4,5];
xj = [5,4,3,2,1];
X = [xi;xj]';
dist = pdist(X,'mahal')
% dist = 0.6325 1.2649 1.8974 2.5298 0.6325 1.2649 1.8974 0.6325 1.2649 0.6325

余弦距离

余弦距离可用来衡量两个向量的差异，其公式如下：

\[dist(x_{i},x_{j})=cos(\theta)=\frac{\sum_{k=1}^{n}x_{ik}x_{jk}}{\sqrt{\sum_{k=1}^{n}x^{2}_{ik}} \sqrt{\sum_{k=1}^{n}x^{2}_{jk}}} \]

夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小，余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1，当两个向量的方向完全相反余弦取最小值-1。

matlab程序如下：

xi = [1,2,3,4,5];
xj = [5,4,3,2,1];
dist = 1 - pdist2(xi,xj,'cosine')
% dist = 0.6364

汉明距离

两个等长字符串s1与s2的汉明距离为：将其中一个变为另外一个所需要作的最小字符替换次数。

"1011101" and "1001001" is 2. 
"2143896" and "2233796" is 3. 
"toned" and "roses" is 3.

汉明重量：是字符串相对于同样长度的零字符串的汉明距离，也就是说，它是字符串中非零的元素个数：对于二进制字符串来说，就是 1 的个数，所以 11101 的汉明重量是 4。因此，如果向量空间中的元素$a$和$b$之间的汉明距离等于它们汉明重量的差$a-b$。

应用：汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。比如在信息编码过程中，为了增强容错性，应使得编码间的最小汉明距离尽可能大。但是，如果要比较两个不同长度的字符串，不仅要进行替换，而且要进行插入与删除的运算，在这种场合下，通常使用更加复杂的编辑距离等算法。

matlab程序如下：

xi = [1,2,3,4,5];
xj = [5,4,3,2,1];
dist = pdist2(xi,xj,'hamming')
% dist = 0.8000

杰卡德距离

杰卡德相似系数：两个集合A和B的交集元素在A，B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示：

\[J(A,B)=\frac{A \bigcap B}{A \bigcup B} \]

杰卡德距离(Jaccard Distance)：与杰卡德相似系数相反，用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度：

\[J_{\delta}(A,B)=1-J(A,B)=\frac{|A \bigcup B|-|A \bigcap B|}{|A \bigcup B|} \]

用公式表示：

\[dist(x_{i},x_{j})=\frac{|x_{i} \bigcup x_{j}|-|x_{i} \bigcap x_{j}|}{| x_{i} \bigcup x_{j} |} \]

matlab程序如下(matlab中将杰卡德距离定义为不同的维度的个数占“非全零维度”的比例)：

xi = [1,2,3,4,5];
xj = [5,4,3,2,1];
dist = pdist2(xi,xj,'jaccard')
% dist = 0.8000

熵

信息熵描述的是整个系统内部样本之间的一个距离，或者称之为系统内样本分布的集中程度(一致程度)，分散程度，混乱程度(不一致程度)。系统内样本分布越分散(或者说分布越平均)，信息熵就越大。分布越有序(或者说分布越集中)，信息熵就越小，公式为：

\[Entropy(X)=\sum_{i=1}^{n}-p_{i}\log_{2}p_{i} \]

其中，$n$是样本集$X$的类别数，$p_{i}$是$X$中第$i$类元素出现的概率。

互信息

设有两个概率分布$X$，$Y$上，$x \in X$，$y \in Y$，则$X$和$Y$的互信息为：

\[I(X,Y)=\sum_{x \in X}\sum_{y \in Y}p(x,y)\log\frac{p(x,y)}{p(x)p(y)} \]

皮尔逊相关系数

设$X$，$Y$是两个随机变量，其
皮尔逊相关系数为：

\[\rho_{X,Y}=\frac{Cov(X,Y)}{\sigma_{X}\sigma_{Y}} \]

其中，$Cov(X,Y)$是$X$，$Y$的协方差，$\sigma_{X}$，$\sigma_{Y}$是$X$，$Y$的标准差。

KL散度

相对熵，$P(x)$，$Q(x)$是两个概率分布，其距离为：

\[D_{KL}(P||Q)=\sum_{i=1}P(x)\log \frac{P(x)}{Q(x)} \]

它是非对称度量：

\[D_{KL}(P||Q) \neq D_{KL}(Q||P) \]

JS距离

基于KL散度发展而来，是对称度量:

\[JSD(P||Q)=\frac{1}{2}D_{KL}(P||M)+\frac{1}{2}D_{KL}(Q||M) \]

其中

\[M = \frac{1}{2}(P+Q) \]

MMD距离

量在再生希尔伯特空间中两个分布的距离，是一种核学习方法。两个随机变量的距离为：

\[MMD(X,Y)=||\sum_{i=1}^{n_{1}}\phi(x_{i})-\sum_{j=1}^{n_{2}}\phi(y_{j})||^{2}_{H} \]

其中，$\phi(\cdot)$是映射，用于把原变量映射到高维空间中。

以上便是一些机器学习里面常见的度量方式，其实还有很多，例如Principal angle，HSIC等，这里就不继续展开叙述了。
针对不同的特征，不同的问题，我们需要选择合适的度量方式。

本文参考了

posted @ 2020-02-24 13:16 Gedanke 阅读(2408) 评论(0) 编辑收藏举报

刷新页面返回顶部

特征与特征距离度量

什么是特征

特征的分类

VDW

欧式距离

标准化欧氏距离

切比雪夫距离

曼哈顿距离

闵可夫斯基距离

马氏距离

余弦距离

汉明距离

杰卡德距离

相关距离

熵

互信息

皮尔逊相关系数

KL散度

JS距离

MMD距离