Mel频谱图与MFCC
这次要讲的是语音处理中常用的特征值 -- Mel频谱图(Mel Spectrogram)和Mel频率倒谱系数(Mel Frequency Cepstrum Coefficient, MFCC)。
什么是Mel?
Mel是S. S. Stevens等人于1937年发表的论文\(^{[1]}\)中定义的一种非线性刻度单位。它的定义是为了反应人类听觉系统对声音频率的主观感知。因为人耳对低频的声音更为敏感,而对高频的声音相对不那么敏感\(^{[2]}\)。换句话说,当处理两个比较相近的频率成分时,人耳无法区分出它们的差异,且这种效应在高频部分更加明显\(^{[3]}\)。这里用“人耳”是图省事,听觉系统这个整体的行为不止只有耳朵参与了。
将线性的频率刻度转化为Mel刻度,可以更好地模拟人类听觉系统的行为,而且大量的实验与工程结果证明了以Mel频谱图为基础的语音特征值能够提高模型在语音识别等任务上的性能。
Mel长什么样?
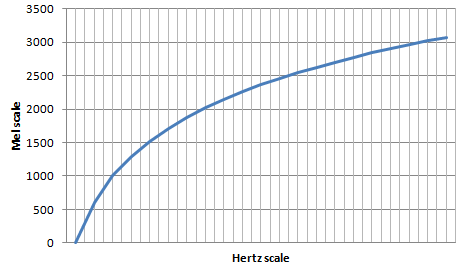
Mel刻度\(m\)与我们常用的频率刻度\(f\)赫兹之间的转换公式为:
\(m=2595 log_{10}(1+\frac{f}{700})\)
对应的曲线为:
Spectrogram -> Mel Spectrogram
在librosa.feature.melspectrogram里,首先是计算普通的spectrogram,然后建立一个从\(f\)到\(m\)的映射,再根据这个映射将spectrogram的频率为Mel频率:
S, n_fft = _spectrogram(
y=y,
S=S,
n_fft=n_fft,
hop_length=hop_length,
power=power,
win_length=win_length,
window=window,
center=center,
pad_mode=pad_mode,
)
# Build a Mel filter
mel_basis = filters.mel(sr=sr, n_fft=n_fft, **kwargs)
melspec: np.ndarray = np.einsum("...ft,mf->...mt", S, mel_basis, optimize=True)
return melspec
这里调用的函数np.einsum()很有意思,能够执行很灵活的矩阵操作。有兴趣的可以去看官方手册。我直接问ChatGPT怎么解释librosa里使用np.einsum()的这一步,得到的回答是:
在librosa库中,np.einsum("...ft,mf->...mt", S, mel_basis, optimize=True)表示使用爱因斯坦求和约定(Einstein summation convention)对S和mel_basis两个数组进行操作,以计算Mel滤波器组在输入频谱(如STFT的幅度谱)上的响应。这里的操作等同于将输入频谱与Mel滤波器组进行矩阵乘法。
首先,了解一下输入参数:
S:一个多维数组,表示输入频谱。例如,它可以是形状为(..., n_fft, n_frames)的幅度谱或功率谱,其中n_fft表示频率(或者说FT bins)的数量,n_frames表示帧的数量,...表示其他可选的维度(例如批次或通道)。
mel_basis:一个二维数组,表示Mel滤波器组。它的形状为(n_mels, n_fft),其中n_mels表示Mel滤波器的数量。
这里的np.einsum()操作:
"...ft,mf->...mt"表示输入数组S的索引为...ft(其他维度、频率和帧),mel_basis的索引为mf(Mel滤波器和频率),输出数组的索引为...mt(其他维度、Mel滤波器和帧)。因为f索引在输入和Mel滤波器组中都存在,所以我们需要对其求和。
optimize=True表示启用优化策略,以提高计算性能。
这个操作的结果是一个多维数组,形状为(..., n_mels, n_frames),表示Mel滤波器组在输入频谱上的响应。这个结果通常用于计算Mel频谱特征(如梅尔频率倒谱系数,MFCC),在语音识别和音频分析任务中非常有用。
图片例子,来源\(^{[4]}\):
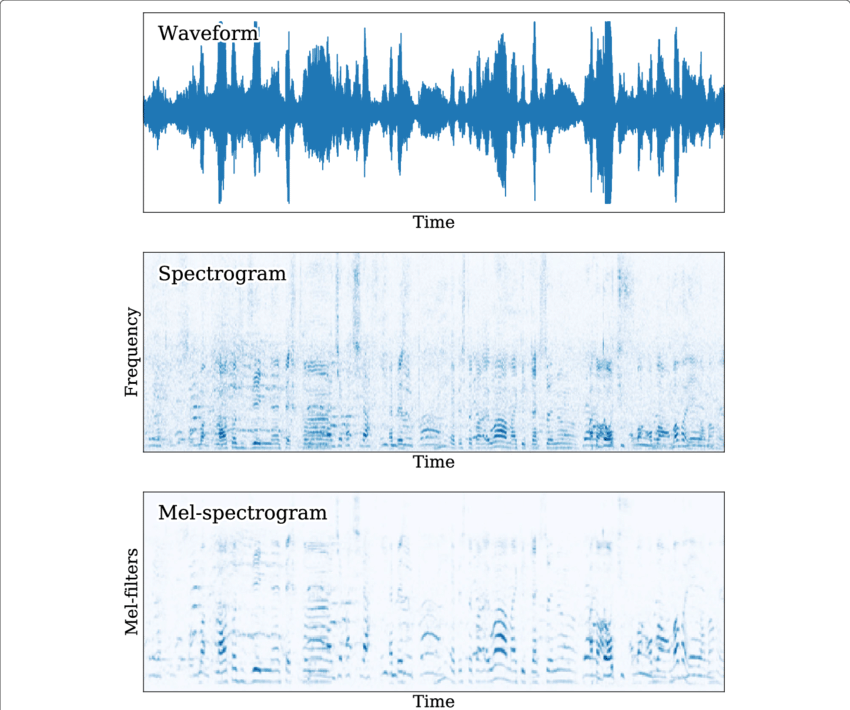
能够看出,原来Spectrogram中相对拥挤至模糊的语音低频部分在Mel Spectrogram中能够更容易的被分辨出来。
MFCC
提取MFCC特征的流程大致为:
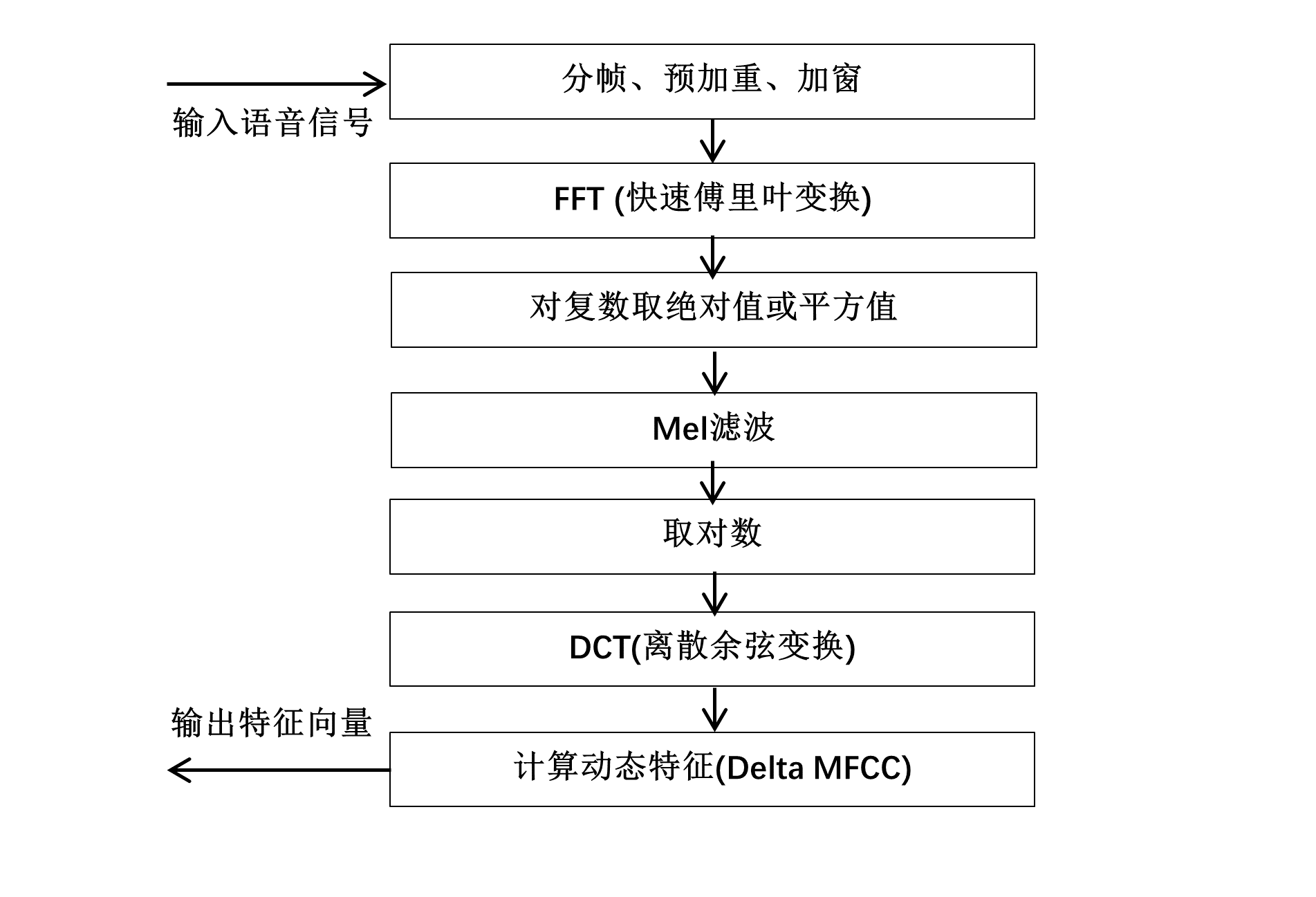
前面三步到取平方值和一般的Spectrogram一样,后面的Mel滤波就是将\(f\)转换为\(m\)。再后面的取对数和DCT,我看到有些讲解是人耳对声音的感受是对数增长的,或者是经滤波后的得到的系数是高度相关的,要进行解相关。
我印象里模糊地记得原理像是这样,但又记得有一个很巧妙,让人眼前一亮的理由。其实这就是名字里的Cepstrum倒谱分析一词。
搜关键词的话能够得到很多这方面的讲解。我个人最喜欢这个图\(^{[2]}\):
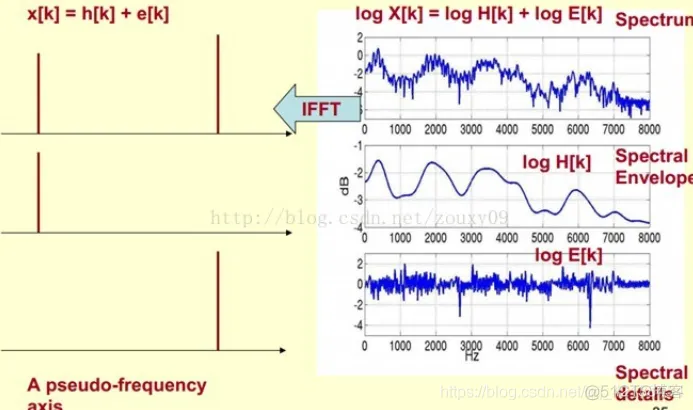
下面是问ChatGPT“人的发声器官和倒谱分析之间的联系”后得到的回答:
是的,人的发声器官和倒谱分析之间存在联系。在语音处理领域,倒谱分析是一种用于分析语音信号的技术,它可以帮助我们分离和识别语音信号中的不同成分,如声源(发声器官产生的声音)和声道(声音在口腔、鼻腔和咽喉等结构中传播的特征)。
人的发声器官主要包括声带、声道和鼻腔等结构。声带通过振动产生声音,然后声音在声道和鼻腔中传播,形成最终的语音信号。在这个过程中,声道和鼻腔等结构对声音产生滤波作用,即调制声音的频谱特征。
倒谱分析通过对语音信号进行处理,可以将声源信息(通常表示为梅尔倒谱系数中的低阶系数)与声道信息(通常表示为梅尔倒谱系数中的高阶系数)分离。这种分离有助于提取有关发声器官的特征,进而用于语音识别、说话人识别、情感分析等任务。
在计算梅尔频率倒谱系数(MFCC)时,我们首先将语音信号转换为梅尔频谱,然后对梅尔频谱应用离散余弦变换(DCT),以将其从频域转换为倒谱域。在倒谱域中,低阶系数主要表示声源信息,而高阶系数主要表示声道信息。通过倒谱分析,我们可以从语音信号中提取与发声器官相关的有用特征。
我的理解是,时域上的语音信号是声源\(h\)和声道\(e\)之间卷积作用后形成的。相对于声道,声源携带的信息更能提供辨识属性\(^{[2]}\)。将语音转换到频域后就是\(H\)与\(E\)相乘,取了对数后就变成了\(H\)与\(E\)相加。且声源\(H\)(频谱的包络)变化较慢,声道\(E\)(频谱的细节)变化较快,那么对这组信号再进行一次DCT(一方面是为了更好地捕捉能量信息,同时也是去相关性),就能将低频和高频成分分离开。通常截取DCT前12维的系数也是为了保留音频信号的主要特征。
题外话
之前我对MFCC的理解是,就是和LFCC差不多的语音特征值中的一种。后来实验里要用adversarial attack,就是通过处理DNN的输入,让它得出相反的分类结果。当我们对语音波形做些手脚后,本来使用波形或者时频Spectrogram的DNN都会受影响而产生相反的分类结果,只是受影响的程度不一样罢了。但是一些很简单的,使用LFCC或者CQCC的模型反而不受影响。
后来我查了相关的资料,对倒谱系数(Cepstral Coefficients)这个词有了更进一步的理解。原谅我接下来作为一个语音从业者的不规范/专业的表述。之前看过有网友的评价是“对发声器官建模”,我一直都不太理解。其实使用倒谱系数的特征值后,一个DNN可以看作是使用X光扫描一个正在说话的人,而使用语音波形或者Spectrogram的DNN能做的只是去听语音。
当我们在语音波形上做了些手脚后,可能这些被处理后的语音听起来会不一样,但它们背后所代表的发声器官可能就变化不大。一个处理Spectrogram的DNN会听出来区别,但一个处理MFCC的DNN却看不出区别。
参考文献
[1] S. S. Stevens, J. Volkmann, E. B. Newman, "A Scale for the Measurement of the Psychological Magnitude Pitch", Journal of the Acoustical Society of America, 1937.
[2] 倒谱分析与MFCC
[3] Mel Frequency Cepstral Coefficient (MFCC) tutorial
[4] D. de Benito, A. Lozano-Diez et al., "Exploring convolutional, recurrent, and hybrid deep neural networks for speech and music detection in a large audio dataset", EURASIP Journal on Audio Speech and Music Processing, 2019.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号