bzoj1407: [Noi2002]Savage（扩欧）

题目描述：

 

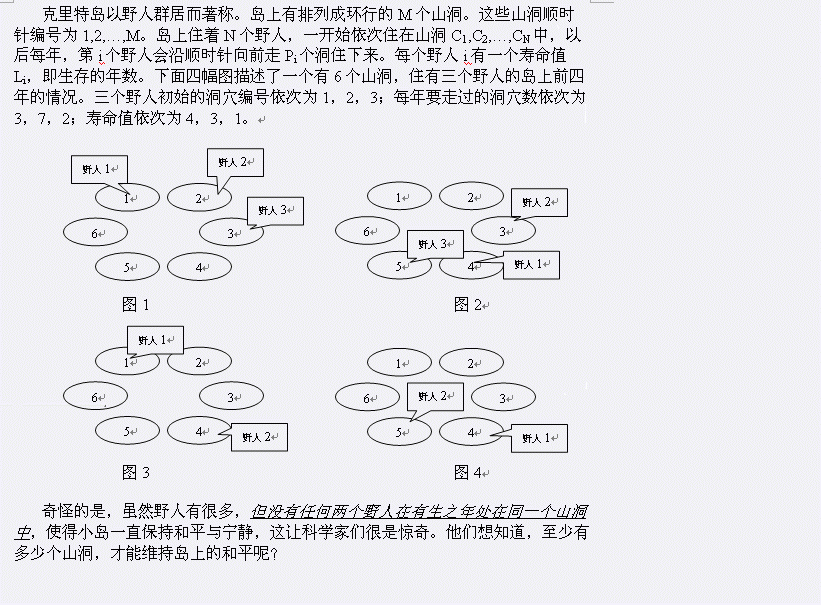
输入格式：第一行一个整数，表示野人的数目。

                 第2~n+行每行三个整数ci, pi, li，表示每个野人初始住的洞穴编号，每年走过的洞穴数和寿命值。

 

输出格式：一个数m表示最少的洞穴数。

 

输入样例：

3
1 3 4
2 7 3
3 2 1

 

输出样例：

6

//该样例对应题目中描述的例子

 

解析：对于每个m，对于每两个野人可以列出式子 c[i] + p[i] * x = c[j] + p[j] * x (mod m)

          转化为方程即为 (p[i] - p[j]) * x + m * k = c[j] - c[i]

          于是用扩欧求解 x 即可，若无解或解出的 x 比两个野人寿命的最小值大，说明两个野人在有生之年不会相会。

          这样判断完每一对野人，若每一对都成立，则说明这个m可行。

          由于数据很小，所以m暴力枚举即可。

 

代码如下：

#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn = 20;
int n, c[maxn], p[maxn], l[maxn], mx, x, y;

int read(void) {
    char c; while (c = getchar(), c < '0' || c >'9'); int x = c - '0';
    while (c = getchar(), c >= '0' && c <= '9') x = x * 10 + c - '0'; return x;
}

int exgcd(int a, int b) { //扩欧 
    if (!b) {
      x = 1; y = 0; return a;
    }
    int d = exgcd(b, a % b);
    int t = x; x = y; y = t - (a / b) * y;
    return d;
}

int pd(int m) {
    for (int i = 1; i <= n; ++ i)
      for (int j = i + 1; j <= n; ++ j) {
          int a = p[i] - p[j], b = m, d = c[j] - c[i];
            if (a < 0) a = -a, d = -d; //由于a为非负数，所以若a<0，则将a变为-a 
          int g = exgcd(a, b);
            if (d % g) continue;
          a /= g; b /= g; d /= g; x *= d; 
          x = (x % b + b) % b; //求最小的正整数解 
          if (!x) x += b;
          if (x <= min(l[i], l[j])) return 0; //不成立，直接退出 
      }
    return 1;
}

int main() {
    n = read();
      for (int i = 1; i <= n; ++ i) c[i] = read(), p[i] = read(), l[i] = read(), mx = max(mx, c[i]); 
      for (int i = mx; i ; ++ i) { //枚举m 
          if (pd(i)) return printf("%d", i);
      }
    return 0;
}