[USACO08DEC]秘密消息Secret Message(trie)
【题目描述】
贝茜正在领导奶牛们逃跑.为了联络,奶牛们互相发送秘密信息.
信息是二进制的,共有M(1≤M≤50000)条.反间谍能力很强的约翰已经部分拦截了这些信息,知道了第i条二进制信息的前bi(l《bi≤10000)位.他同时知道,奶牛使用N(1≤N≤50000)条密码.但是,他仅仅了解第J条密码的前cj(1≤cj≤10000)位.
对于每条密码J,他想知道有多少截得的信息能够和它匹配.也就是说,有多少信息和这条密码有着相同的前缀.当然,这个前缀长度必须等于密码和那条信息长度的较小者.
在输入文件中,位的总数(即∑Bi+∑Ci)不会超过500000.
【输入输出格式】
输入:
第1行:两个整数M和N
第2~M+1行:描述了所拦截的信息,第一个为信息的长度len,之后len个01串表示长度为len的密码,每个0与1之间以一个空格隔开。
第M+2~M+N+1行:描述了密码,第一个为密码的长度len,之后len个01串表示长度为len的密码,每个0与1之间以一个空格隔开。
输出:
第1~M行,每行表示密码可以匹配的信息个数。
【输入输出样例】
输入样例:
4 5 3 0 1 0 1 1 3 1 0 0 3 1 1 0 1 0 1 1 2 0 1 5 0 1 0 0 1 2 1 1
输出样例:
1 3 1 1 2
解析:题目要求求拥有公共前缀的信息个数,很容易想到用trie来解决。
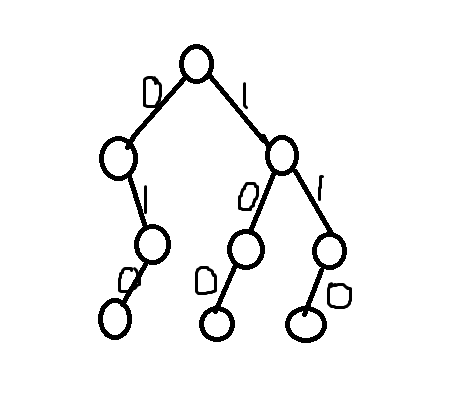
于是可以将输入的信息构建成一个trie,如图:
可是显然光是这样是不够的,所以我们可以在每个节点上记录下有多少个信息的前缀到达了这个节点。
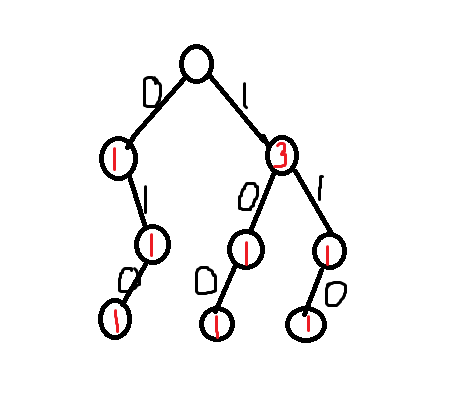
于是,我们得到了这么一个图(根节点不必记录):
现在,在询问读入之后,在trie中扫描读入的密码,走密码串中所表示的路径,答案为各个走过节点的最大值。
如果遇到了节点的分支,则将答案减去另一分支(如果有的话)的节点值。
例如样例中的 0 1
首先找到trie中的0,ans=1;
再在0的下面找到节点1,ans=1;
所以答案即为1;
又如样例中的 1 1
先在trie中找到1,ans=3;
这时,发现节点出现了分叉,需要走的节点是右子节点,那么将答案减去另一分支0的值,则ans=3-1=2;
最后来到节点1,ans=max(1,2)=2;
所以答案为2;
如此,便可以找出公共前缀的个数。
代码如下:
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 5 int m,n,cnt=1; //cnt表示节点的个数 6 int tr[500001][2],val[500001]; 7 8 int read(void) { //读入优化 9 char c; while (c=getchar(),c<'0' || c>'9'); int x=c-'0'; 10 while (c=getchar(),c>='0' && c<='9') x=x*10+c-'0'; return x; 11 } 12 13 int main() { 14 m=read(); n=read(); 15 for (int i=1;i<=m;++i) { 16 int x=read(); 17 int u=1; 18 for (int j=1;j<=x;++j) { 19 int num=read(); 20 if (!tr[u][num]) tr[u][num]=++cnt; //构建trie树 21 u=tr[u][num]; val[u]++; //val数组表示本节点的值 22 } 23 } 24 for (int i=1;i<=n;++i) { 25 int x=read(); 26 int u=tr[1][read()],ans=val[u]; 27 for (int j=2;j<=x;++j) { 28 int num=read(); 29 if (tr[u][num^1]) ans-=val[tr[u][num^1]];//0^1=1,1^1=0,num^1表示另一个子节点 30 else ans=max(ans,val[tr[u][num]]); 31 u=tr[u][num]; //继续往下走 32 } 33 printf("%d\n",ans); 34 } 35 return 0; 36 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号