[BZOJ1500][NOI2005]维修数列

[NOI2005]维修数列

题面

请写一个程序，要求维护一个数列，支持以下 6 种操作：

请注意，格式栏 中的下划线‘ _ ’表示实际输入文件中的空格

Input

输入的第1 行包含两个数N 和M(M ≤20 000)，N 表示初始时数列中数的个数，M表示要进行的操作数目。
第2行包含N个数字，描述初始时的数列。
以下M行，每行一条命令，格式参见问题描述中的表格。
任何时刻数列中最多含有500 000个数，数列中任何一个数字均在[-1 000, 1 000]内。
插入的数字总数不超过4 000 000个，输入文件大小不超过20MBytes。

Output

对于输入数据中的GET-SUM和MAX-SUM操作，向输出文件依次打印结果，每个答案（数字）占一行。

Sample Input

9 8 2 -6 3 5 1 -5 -3 6 3 GET-SUM 5 4 MAX-SUM INSERT 8 3 -5 7 2 DELETE 12 1 MAKE-SAME 3 3 2 REVERSE 3 6 GET-SUM 5 4 MAX-SUM

Sample Output

-1 10 1 10

Hint

思路

这一看就是道裸的splay上区间修改。自己就不造轮子了。引用一下Rain Air神仙的介绍：Splay 如何维护区间信息

Splay 如何维护区间信息——引自Rain Air

如何维护区间

我们都知道平衡树是一种很神奇的东西，可以用于维护动态的序列总信息，但是如果想维护其中的某一个区间的信息，我们该怎么做好呢？
我们考虑换一种维护方式：平衡树的结构不是按照节点的值的大小来进行建树，而是以这个节点在序列中的位置为关键字来维护。也就是说对于平衡树中任意一个节点 \(x\) ，左子树中的元素永远在它前面，右子树的元素永远在它后面。显然一个区间可以对应一个子树，所以我们要使用能提取子树的数据结构，比如 Splay 和 非旋 Treap。
比如我们考虑提取 \([l,r]\)的区间信息：我们首先将 \(l−1\)节点旋转到根，Splay 变成了这样：

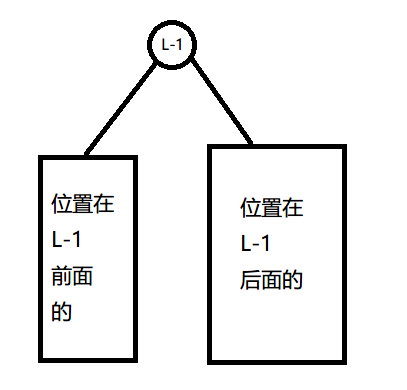
然后我们接着把 \(r+1\) 旋转到 \(l−1\) 的下方，也就变成了这样：

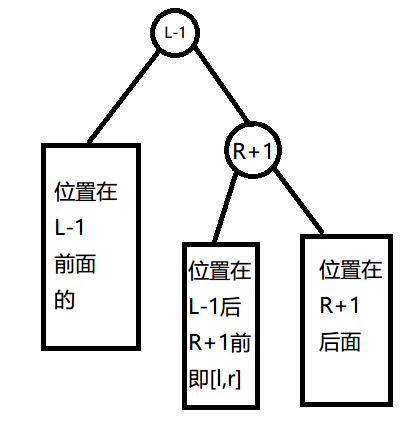
我们发现 \(R+1\) 节点的左子树就是我们要的区间！所以我们直接对这个子树进行想要的操作即可，复杂度是旋转的复杂度即均摊\(O(logn)\)。

Insert 操作

看起来暴力插入所有的数非常不可取。。。随便就能卡掉的样。
我们不妨考虑一下如果我们有了一个序列里的所有的树，想得到这个序列对应的 Splay 可以有什么方便的方法。显然我们可以直接暴力递归建树，这样不仅快 (\(O(nlogn)\)) 得到的树也十分平衡。具体建树过程就是每次选择中点作为当前的根，然后递归处理中点左边和右边。
我们不妨把输入的序列先搞个 Splay 出来，然后我们发现在 x 后插入，如果我们按照上面的方法提取出区间 \([x,x+1]\)，那么 \(x+1\) 的左子树不就应该是我们新建出来的 Splay 吗。。。直接接上去就可以了。

Delete 操作

和 Insert 操作相同的思路：我们直接把这段区间提取出来，不过我们发现现在我们是要删除，所以直接断开这个区间代表的子树与父节点的连接就可以了。但是在这题中为了节省运行空间建议写一个内存回收池来回收这些被删除的节点，这个操作甚至比插入还简单。

MAKE-SAME 操作

考虑把这一段区间修改成同一个数。在线段树上区间操作我们有 lazy-tag 可用，在平衡树上也可以。我们提取出这个区间，然后在根节点打个区间覆盖的标记就行了。注意每次访问这个区间前标记必须要下放。

翻转

学过 LCT 的都会，没学过的参考一下文艺平衡树的做法就可以了。
我们发现建出的 Splay 同时保留了原来序列的性质：如果我们中序遍历这棵 Splay，那么得到的序列就是原序列！我们考虑区间翻转意味着什么：是不是就是对于这个区间里的每一个节点左右儿子都互换啊（因为互换后现在先遍历的是原来后遍历的，并且子树也都交换了）。所以我们同时维护一下翻转标记就可以了。
注意到下放标记的时候如果又有区间覆盖的标记又有翻转的标记，这时候我们可以忽略翻转标记（因为你都是一个数了翻转没有意义），这样能优化不少常数。

求和

我们对于 Splay 的每一个节点，维护它及其它子树中所有节点代表的原序列中的元素的和。查询的时候提取区间直接输出就可以了。

求最大子列

我们考虑一种基于分治的求最大子列方法：对于每个区间都维护从左边开始的最大子列，从右边开始的最大子列和该区间的最大子列，分别记为 \(ls,rs,ans\)。
对于 ls 的维护：我们考虑从左边开始的最大子列是否覆盖了整个左儿子代表的区间，rs 同理。
对于 ans 就有多种可能了：全都在左儿子区间的，全都在右儿子区间的，跨过中间点的。
Push_Up的时候分别维护即可，可以 $O(1) $维护。

以上内容引自Rain Air神仙Splay 如何维护区间信息

代码

只写了几个操作。。。。先去切主席树了QAQ

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<cstring>
#include<string>
#define inf (int)(1e9+10000)
#define maxn 600000
#define extra 501000
using namespace std;
queue<int>recycle;
int idx,n,m;
int a[maxn],id[maxn],root;
int size[maxn],num[maxn],sum[maxn],fa[maxn],son[maxn][2],cnt[maxn];
void push_up(int x){//size and sum
	size[x]=cnt[x];sum[x]=num[x];
	if(son[x][0]){
		size[x]+=size[son[x][0]];
		sum[x]+=sum[son[x][0]];
	}
	if(son[x][1]){
		size[x]+=size[son[x][1]];
		sum[x]+=sum[son[x][1]];
	}
	return;
}
void build(int l,int r,int now,int f){
	if(r<l)return;
	int main_now=id[now],main_fa=id[f];//id on the main tree
	fa[main_now]=main_fa;num[main_now]=a[now];son[main_fa][now>f]=main_now;cnt[main_now]=1;
	if(l==r){
		push_up(main_now);
		return;
	}
	int mid=(l+r)>>1;
	build(l,mid-1,(l+mid-1)>>1,now);
	build(mid+1,r,(mid+1+r)>>1,now);
	push_up(main_now);
	return;
}
void rotate(int x){
	int y=fa[x],z=fa[y],o=(son[y][1]==x);
	son[y][o]=son[x][o^1];
	fa[son[x][o^1]]=y;

	son[x][o^1]=y;
	fa[y]=x;
	
	son[z][son[z][1]==y]=x;
	fa[x]=z;
	push_up(y);
	push_up(x);
	return;
}
void splay(int x,int v=0){
	for(int y;fa[x]!=v;rotate(x)){
		y=fa[x];
		if(fa[y]!=v){
			rotate((son[fa[y]][0]==y)^(son[fa[x]][0]==x)?x:y);
		}
	}
	if(!v)root=x;
}
int kth(int x,int k){
	if(k<=size[son[x][0]]){
		return kth(son[x][0],k);
	}
	if(k<=size[son[x][0]]+cnt[x]){
		return x;
	}
	return kth(son[x][1],k-size[son[x][0]]-cnt[x]);
}
int pre_work(int l,int r){//将序列上的l，r转到对应位置
	int idl=kth(root,l);
	int idr=kth(root,r);
	splay(idl);splay(idr,root);
	return son[son[root][1]][0];
}
int q_sum(int l,int r){//操作序列上l和r求和
	int x=pre_work(l-1,r+1);push_up(x);//test
	return sum[x];
}
void insert(int pos,int tot){
	for(int i=1;i<=tot;i++)scanf("%d",&a[i]);
	for(int i=1;i<=tot;i++){
		if(!recycle.empty()){
			id[i]=recycle.front();recycle.pop();
		}
		else{
			id[i]=++idx;
		}
	}
	pre_work(pos+1,pos+2);
	int f=son[root][1];
	id[extra]=f;
	int port=(1+tot)>>1;	
	build(1,tot,port,extra);
	son[son[root][1]][0]=id[port];
	return;
}
int	main(){
	freopen("in","r",stdin);
	scanf("%d%d",&n,&m);id[1]=1;id[n+2]=n+2;a[1]=a[n+2]=-inf;
	for(int i=1;i<=n;i++){scanf("%d",&a[i+1]);id[i+1]=i+1;}
	idx=n+2;
	build(1,idx,(1+idx)>>1,0);//build up a tree in the rule of BST.
	//the root of this subtree is id[(1+n)>>1]
	root=id[(1+idx)>>1];
	/*-------------init done--------------*/
	for(int i=1;i<=m;i++){
		char type[30];scanf("%s",type);
		if(type[0]=='M'&&type[2]=='X'){//max-sum
			continue;
		}
		int pos,tot;scanf("%d%d",&pos,&tot);
		if(type[0]=='G'){//get sum
			printf("%d\n",q_sum(pos+1,pos+tot-1+1));
		}
		else if(type[0]=='I'){//insert
			insert(pos,tot);
		}
	}
	return 0;
}