LeetCode-450. 删除二叉搜索树中的节点

题目来源

450. 删除二叉搜索树中的节点

题目描述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

输入： root = [5,3,6,2,4,null,7], key = 3
输出： [5,4,6,2,null,null,7]
解释： 给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
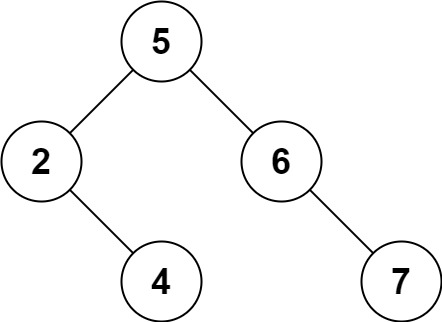
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

• 节点数的范围 [0, 104].
• -105 <= Node.val <= 105
• 节点值唯一
• root 是合法的二叉搜索树
• -105 <= key <= 105

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

题解分析

解法一：中序遍历

情况 1：A 恰好是末端节点，两个子节点都为空，那么它可以当场去世了：

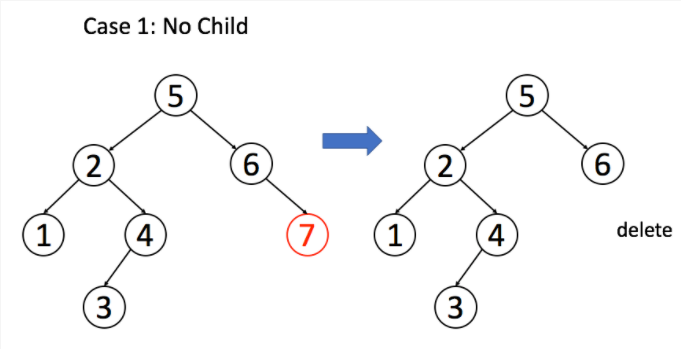
情况 2：A 只有一个非空子节点，那么它要让这个孩子接替自己的位置：

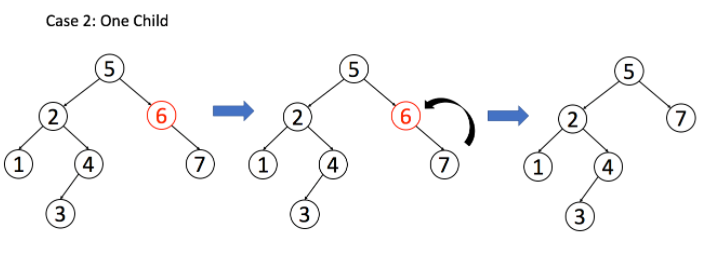
情况 3：A 有两个子节点，麻烦了，为了不破坏 BST 的性质，A 必须找到左子树中最大的那个节点或者右子树中最小的那个节点来接替自己，我的解法是用右子树中最小节点来替换：

/**
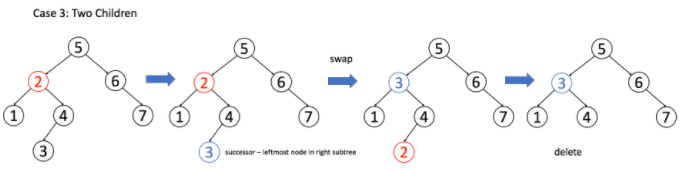
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    // 删除时使用左子树中的最大值替代删除的节点
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root == null){
            return null;
        }else if(root.val > key){
            root.left = deleteNode(root.left, key);
        }else if(root.val < key){
            root.right = deleteNode(root.right, key);
        }else{
            if(root.left == null){
                return root.right;
            }
            if(root.right == null){
                return root.left;
            }
            TreeNode leftMax = getLeftMax(root.left);
            root.left = deleteNode(root.left, leftMax.val);
            leftMax.left = root.left;
            leftMax.right = root.right;
            root = leftMax;
        }
        return root;
    }

    private TreeNode getLeftMax(TreeNode root){
        while(root.right != null){
            root = root.right;
        }
        return root;
    }
}