二分法总结-上下边界确定-指针移动规则
绪论
二分法是用于查找有序序列中某个元素的常用方法，时间复杂度为log(n)
写过二分法的人就知道，二分法好用但是也经常让人头疼，因其边界往往容易出错，而且在刷力扣看题解的时候，一会儿while(left < right)一会儿while(left <= right)，头都搞晕了，因此特地来学习总结一番
最容易出错的地方:
- while循环中到底是 小于 还是 小于等于
- 左右边界left和right，到底是+1 呢，还是要-1呢
这两个问题的本质是一样的，取决于你如何定义左右区间，可以分为两种：
边界开闭的确定
左闭右开
定义左边界left=0，右边界right=arr.length，由于数组的索引范围为0到arr.length-1，right=arr.length这个索引是越界的，所以你相当于定义了一个左闭右开的区间，[left,right)
所以你想想，是while(left < right)还是while(left <= right)，如果说是后者，也就是left和right相等循环也能执行，那么当left=right=arr.length时也能进入循环，那数组不就越界了？
因此，当你定义的区间为左闭右开时，while里面一定是小于
第一个问题解决了，第二个问题我们进入代码说明，talk is cheap, show me the code
现在要从一个有序数组arr[n]中查找某个元素，代码如下：
public int binarySearch(int[] arr, int target){
int left = 0, right = arr.length;
while(left < right){
// 等同于(left+right)/2，但是当left和right较大时两者相加容易发生溢出
int mid = left + (right-left) / 2;
if(arr[mid] == target){
// 找到了target就直接返回mid
return mid;
}else if(arr[mid] > target){
// 如果当前值大于target，而数组是升序的，说明target在数组的左半边[left,mid-1]，但是由于区间定义是左闭右开，因此数组左半边写成[left,mid)，所以right=mid
right = mid;
}else {
// 最后，如果当前值小于target，则说明target在数组的右半边[mid+1,right)，因此left直接等于mid+1就好了
left = mid + 1;
}
}
// 找不到就返回-1
return -1;
}
左闭右闭
思路和上面差不多，只不过是定义的区间变了，因此我在这里简要说明一下
定义左边界left=0，右边界right=arr.length-1，这个时候左右边界均在arr索引范围内，因此是左闭右闭的，[left,right]
因此是while(left <= right)，即便是到了right边界，也不会发生数组溢出
这里我不单独贴出左闭右闭的代码，而是将两个写法的代码进行对比：
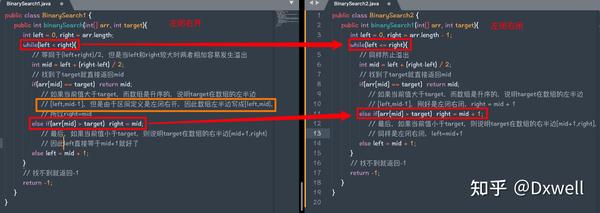
到这里，基本上就可以搞懂边界问题了
我强烈建议你使用左闭右闭这样的区间定义，也就是while(left <= right)，不容易出错
上下边界问题
没有重复元素的就是上面的写法，这里着重讲一下最常用的有重复元素的序列
那我习惯左闭右闭的区间定义，这里用左闭右闭
找有重复元素的target又可以分为两种，比如arr[1,2,2,2,3]，我要找2，那你是想找最左边的2还是最右边的2呢？可以称之为下边界和上边界
上边界
// 下边界，也就是数组中第一次出现target的位置
public int binarySearchLowwer(){
int left = 0;
int right = arr.legth - 1;
int pos = -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] >= target) {
// 中间的值要是大于target肯定往左区间找，如果中间值等于target呢
// 因为我们是找下边界，所以也是往左区间搜索，因此这两种情况可以合并
// 中间值大于等于target都往左区间[left,mid-1]查找
pos = mid; // pos会被不断的往左更新，直到为下边界
right = mid - 1;
}
else {
// 这个简单，中间的数小于target，往右子区间[mid+1,right]查找
left = mid + 1;
}
}
return pos;
}
下边界
// 上边界，也就是数组中最后一次出现target的位置
public int binarySearchUpper(){
int left = 0;
int right = arr.legth - 1;
int pos = -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] > target) {
// 中间的值要是大于target肯定往左区间找，如果中间值等于target呢
// 因为我们是找上边界，所以肯定往又区间找，所以放到else情况里面
right = mid - 1;
}
else {
// 中间的数小于等于target，往右子区间[mid+1,right]查找
pos = mid; // pos会被不断的往左更新，直到为下边界
left = mid + 1;
}
}
return pos;
}
可以观察到，上边界和下边界只有两处代码不同
- 下边界arr[mid]大于等于target，上边界arr[mid]大于target
- pos的位置不一样
