LeetCode-354. 俄罗斯套娃信封问题
题目来源
题目详情
给你一个二维整数数组 envelopes ，其中 envelopes[i] = [wi, hi] ，表示第 i 个信封的宽度和高度。
当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。
请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。
注意：不允许旋转信封。
示例 1：
输入： envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出： 3
解释： 最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
示例 2：
输入： envelopes = [[1,1],[1,1],[1,1]]
输出： 1
提示：
1 <= envelopes.length <= 105envelopes[i].length == 21 <= wi, hi <= 105
题解分析
解法一：常规动态规划
- 本题其实是二维的【最长递增子序列】问题，因为一个信封要想套另一个信封，那么外层的信封长和宽均需要严格大于内层信封。
- 假设信封是由 (w, h) 这样的二维数对形式表示的，思路如下：先对宽度 w 进行升序排序，如果遇到 w 相同的情况，则按照高度 h 降序排序。之后把所有的 h 作为一个数组，在这个数组上计算 LIS 的长度就是答案。
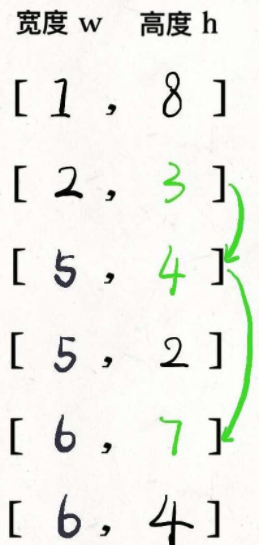
- 画个图理解一下，先对这些数对进行排序：
- 然后在 h 上寻找最长递增子序列：
class Solution {
public int maxEnvelopes(int[][] envelopes) {
int n = envelopes.length;
Arrays.sort(envelopes, (int[] env1, int[] env2) -> {
// 按照宽度升序，如果宽度相同则按照高度降序
if(env1[0] != env2[0]){
return env1[0] - env2[0];
}else{
return env2[1] - env1[1];
}
});
// dp[i]表示以i结尾的子数组的最长递增子序列
int[] dp = new int[n];
int maxs = 1;
for(int i=0; i<n; i++){
dp[i] = 1;
for(int j=0; j<i; j++){
if(envelopes[i][1] > envelopes[j][1]){
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
maxs = Math.max(maxs, dp[i]);
}
return maxs;
}
}
解法二：二分+动态规划
第一种方法的时间复杂度是\(O(n^2)\)，对于本题的数据量来说必定会超时，所以需要一种更优的解法。
这个解法的时间复杂度为 O(NlogN)，但是说实话，正常人基本想不到这种解法（也许玩过某些纸牌游戏的人可以想出来）。所以大家了解一下就好，正常情况下能够给出动态规划解法就已经很不错了。
根据题目的意思，我都很难想象这个问题竟然能和二分查找扯上关系。其实最长递增子序列和一种叫做 patience game 的纸牌游戏有关，甚至有一种排序方法就叫做 patience sorting（耐心排序）。
为了简单起见，后文跳过所有数学证明，通过一个简化的例子来理解一下算法思路。
首先，给你一排扑克牌，我们像遍历数组那样从左到右一张一张处理这些扑克牌，最终要把这些牌分成若干堆。
处理这些扑克牌要遵循以下规则：
只能把点数小的牌压到点数比它大的牌上；如果当前牌点数较大没有可以放置的堆，则新建一个堆，把这张牌放进去；如果当前牌有多个堆可供选择，则选择最左边的那一堆放置。
比如说上述的扑克牌最终会被分成这样 5 堆（我们认为纸牌 A 的牌面是最大的，纸牌 2 的牌面是最小的）。
为什么遇到多个可选择堆的时候要放到最左边的堆上呢？因为这样可以保证牌堆顶的牌有序（2, 4, 7, 8, Q），证明略。
按照上述规则执行，可以算出最长递增子序列，牌的堆数就是最长递增子序列的长度，证明略。
我们只要把处理扑克牌的过程编程写出来即可。每次处理一张扑克牌不是要找一个合适的牌堆顶来放吗，牌堆顶的牌不是有序吗，这就能用到二分查找了：用二分查找来搜索当前牌应放置的位置。
PS：旧文 二分查找算法详解详细介绍了二分查找的细节及变体，这里就完美应用上了，如果没读过强烈建议阅读。
public int lengthOfLIS(int[] nums) {
int[] top = new int[nums.length];
int piles = 0;
for (int i = 0; i < nums.length; i++) {
int poker = nums[i];
int left = 0, right = piles;
while (left < right) {
int mid = (left + right) / 2;
if (top[mid] > poker) {
right = mid;
} else if (top[mid] < poker) {
left = mid + 1;
} else {
right = mid;
}
}
if (left == piles) piles++;
top[left] = poker;
}
return piles;
}
至此，二分查找的解法也讲解完毕。
