LeetCode-221. 最大正方形

题目来源

221. 最大正方形

题目详情

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

输入： matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出： 4

示例 2：

输入： matrix = [["0","1"],["1","0"]]
输出： 1

示例 3：

输入： matrix = [["0"]]
输出： 0

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] 为 '0' 或 '1'

题解分析

暴力法

1. 乍一看，本题和前面做过的85. 最大矩形十分相似。最大矩形那题是求解最大矩形，而这题则是求解最大正方形。而我们知道，正方形是矩形的一种特例，所以上一题的方法也能用在这题中。
2. 本题的暴力法相对于上一题的暴力法有点区别，就是当计算面积时，不是使用长乘宽，而是用长宽中的较小者作为边长求解面积。

class Solution {
    public int maximalSquare(char[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        int[][] width = new int[n][m];
        int maxarea = 0;
        for(int i=0; i<n; i++){// 遍历每一行
            for(int j = 0; j<m ;j++){
                // 求出以当前元素结尾的位置，其行前面连续1的个数
                if(matrix[i][j] == '1'){
                    if(j == 0){
                        width[i][j] = 1;
                    }else{
                        width[i][j] = width[i][j-1] + 1;
                    }
                }else{
                    width[i][j] = 0;
                }

                // 向上延伸，找到同一列的width最小值作为宽度，递增计数器作为高度
                int height = 0;
                int minwidth = Integer.MAX_VALUE;
                for(int row = i; row >=0; row--){
                    if(width[row][j] > 0){
                        minwidth = Math.min(minwidth, width[row][j]);
                        height++;
                        int square = Math.min(minwidth, height);
                        maxarea = Math.max(maxarea, square * square);
                    }else{
                        break;
                    }
                }
            }
        }
        return maxarea;
    }
}

解法二：动态规划

1. 本题的最优解法还是需要使用动态规划，因为方法一虽然直观，但是时间复杂度太高，有没有办法降低时间复杂度呢？
2. 可以使用动态规划降低时间复杂度。我们用 dp(i, j) 表示以 (i, j) 为右下角，且只包含 1 的正方形的边长最大值。如果我们能计算出所有 dp(i, j) 的值，那么其中的最大值即为矩阵中只包含 1 的正方形的边长最大值，其平方即为最大正方形的面积。
3. 那么如何计算 dp 中的每个元素值呢？对于每个位置 (i, j)，检查在矩阵中该位置的值：
   • 如果该位置的值是 0，则 dp(i, j)=0，因为当前位置不可能在由 1 组成的正方形中；
   • 如果该位置的值是 1，则 dp(i, j) 的值由其上方、左方和左上方的三个相邻位置的 dp 值决定。具体而言，当前位置的元素值等于三个相邻位置的元素中的最小值加 1，状态转移方程如下：
     \(dp(i, j)=min(dp(i−1, j), dp(i−1, j−1), dp(i, j−1))+1\)
4. 此外，还需要考虑边界条件。如果 i 和 j 中至少有一个为 0，则以位置 (i, j) 为右下角的最大正方形的边长只能是 1，因此 dp(i, j)=1。

class Solution {
    public int maximalSquare(char[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        int[][]dp = new int[n][m];
        int maxside = 0;
        for(int i=0; i<n; i++){// 遍历每一行
            for(int j = 0; j<m ;j++){
                if(matrix[i][j] == '1'){
                    if(i == 0 || j == 0){
                        dp[i][j] = 1;
                    }else{
                        dp[i][j] = Math.min(dp[i-1][j], Math.min(dp[i-1][j-1], dp[i][j-1])) + 1;
                    }
                    maxside = Math.max(maxside, dp[i][j]);
                }
            }
        }
        return maxside * maxside;
    }
}

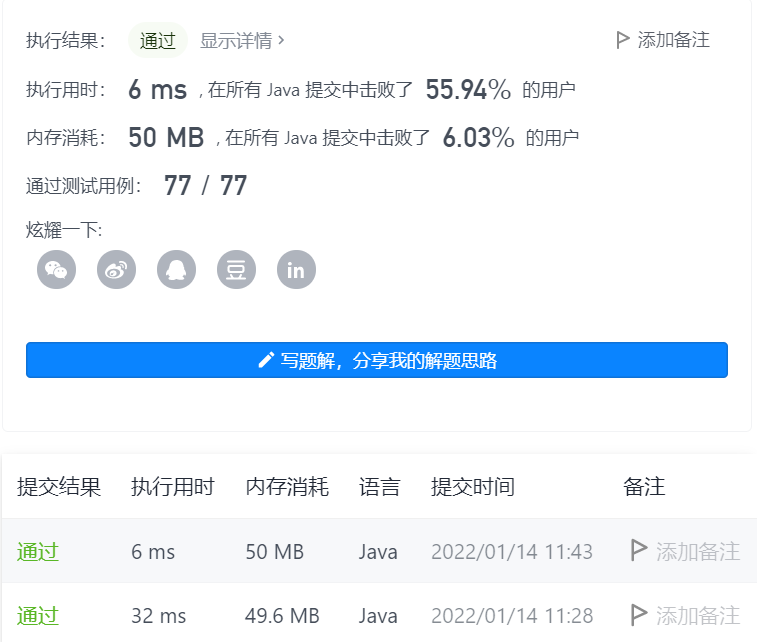
结果展示