LeetCode-85. 最大矩形

题目来源

85. 最大矩形

题目详情

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

输入： matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出： 6
解释： 最大矩形如上图所示。

示例 2：

输入： matrix = []
输出： 0

示例 3：

输入： matrix = [["0"]]
输出： 0

示例 4：

输入： matrix = [["1"]]
输出： 1

示例 5：

输入： matrix = [["0","0"]]
输出： 0

提示：

• rows == matrix.length
• cols == matrix[0].length
• 1 <= row, cols <= 200
• matrix[i][j] 为 '0' 或 '1'

题解分析

暴力解法

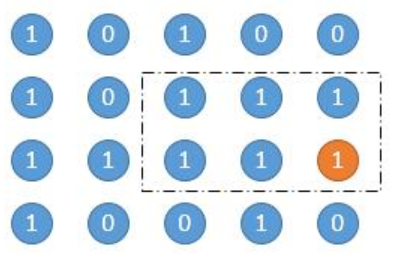
1. 遍历每个点，求以这个点为矩阵右下角的所有矩阵面积。如下图的两个例子，橙色是当前遍历的点，然后虚线框圈出的矩阵是其中一个矩阵。
   
2. 但是如何找到这个矩形呢？这里有一个讨巧的方法，即为每个位置记录一次以该元素结尾的，当前行中相应位置前面连续出现的1的个数。
   
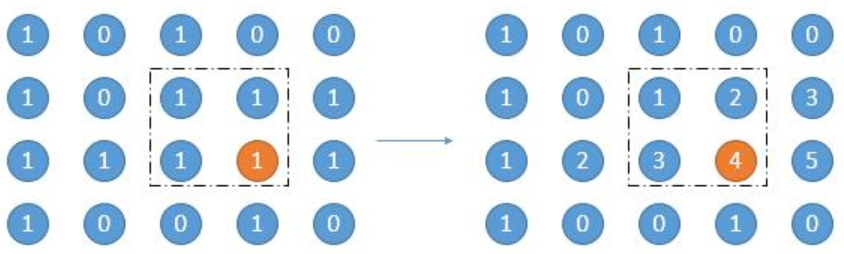
3. 对于具体的矩形最大面积的求法，则可以参照下列步骤：
   • 首先求出高度是 1 的矩形面积，也就是它自身的数，如图中橙色的 4，面积就是 4。
   • 然后向上扩展一行，高度增加一，选出当前列最小的数字，作为矩阵的宽，求出面积，对应上图的矩形框。
   • 然后继续向上扩展，重复步骤 2。
4. Java代码实现如下：

class Solution {
    public int maximalRectangle(char[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        int[][] width = new int[n][m];
        int maxarea = 0;
        for(int i=0; i<n; i++){// 遍历每一行
            for(int j = 0; j<m ;j++){
                // 求出以当前元素结尾的位置，其行前面连续1的个数
                if(matrix[i][j] == '1'){
                    if(j == 0){
                        width[i][j] = 1;
                    }else{
                        width[i][j] = width[i][j-1] + 1;
                    }
                }else{
                    width[i][j] = 0;
                }

                // 向上延伸，找到同一列的width最小值作为宽度，递增计数器作为高度
                int height = 0;
                int minwidth = Integer.MAX_VALUE;
                for(int row = i; row >=0; row--){
                    if(width[row][j] > 0){
                        minwidth = Math.min(minwidth, width[row][j]);
                        height++;
                        maxarea = Math.max(maxarea, minwidth * height);
                    }else{
                        break;
                    }
                }
            }
        }
        return maxarea;
    }
}

解法二：单调栈

1. 本题同样可以使用单调栈来极大简化问题的求解，而在前面做过的题目中，我们已经会初步使用单调栈了，这里可以参考LeetCode-84. 柱状图中最大的矩形的题解来回顾单调栈的使用方法。
2. 再想一下这个题，看下边的橙色的部分，这完全就是上一道题呀！
   
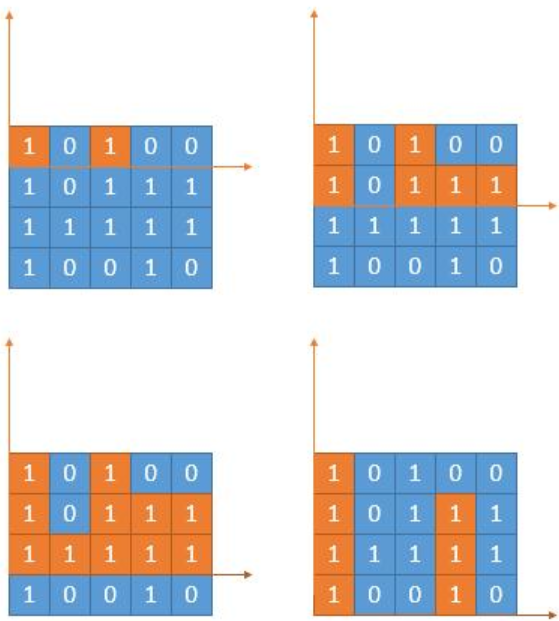
3. 算法有了，就是求出每一层的 heights[] 然后传给上一题的函数就可以了。
4. Java代码实现：

class Solution {
    public int maximalRectangle(char[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        int[] heights = new int[m];
        int maxarea = 0;
        for(int i=0; i<n; i++){// 遍历每一行
            // 求出每一列的高度
            for(int j = 0; j<m ;j++){
                if(matrix[i][j] == '1'){
                    heights[j] += 1;
                }else{
                    heights[j] = 0;
                }
            }
            maxarea = Math.max(maxarea, largestRectangleArea(heights));
        }
        return maxarea;
    }
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        Deque<Integer> sta = new LinkedList<>();
        int maxs = Integer.MIN_VALUE;
        // 从左往右考虑
        for(int i=0; i<n; i++){
            // 从右往左考虑可以出栈的元素
            while(!sta.isEmpty() && heights[sta.peekFirst()] > heights[i]){
                int curh = heights[sta.pollFirst()];
                // 处理相同高度的情况，相同高度的矩形一起考虑
                while(!sta.isEmpty() && heights[sta.peekFirst()] == curh){
                    sta.pollFirst();
                }
                int width = 0;
                if(sta.isEmpty()){// 当前高度是目前为止所有矩形中最低的，计算整个宽度
                    width = i;
                }else{
                    width = i - sta.peekFirst() - 1;// 计算矩形的宽度
                }
                maxs = Math.max(maxs, width * curh);
            }
            // 最新高度进栈
            sta.addFirst(i);
        }
        // 假设数组中有第n个矩形，它的高度为0
        while(!sta.isEmpty()){
            int curh = heights[sta.pollFirst()];
            // 处理相同高度
            while(!sta.isEmpty() && heights[sta.peekFirst()] == curh){
                sta.pollFirst();
            }
            int width = 0;
            if(sta.isEmpty()){// 当前高度是目前为止所有矩形中最低的，计算整个宽度
                width = n;
            }else{
                width = n - sta.peekFirst() - 1;// 计算矩形的宽度
            }
            maxs = Math.max(maxs, width * curh);
        }
        return maxs;
    }
}

结果展示

参考

1. 详细通俗的思路分析，多解法
2. LeetCode-84. 柱状图中最大的矩形