4. 寻找两个正序数组的中位数 + 二分法

题目来源

LeetCode_4

题目描述

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入： nums1 = [1,3], nums2 = [2]
输出： 2.00000
解释： 合并数组 = [1,2,3] ，中位数 2

示例 2：

输入： nums1 = [1,2], nums2 = [3,4]
输出： 2.50000
解释： 合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示：

• nums1.length == m
• nums2.length == n
• 0 <= m <= 1000
• 0 <= n <= 1000
• 1 <= m + n <= 2000
• -106 <= nums1[i], nums2[i] <= 106

题解分析

解法一：暴力法-先合并两个数组找中位数

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        int len = m + n;
        int right = len >> 1;
        int left = right - 1;
        if((len & 1) == 1)
            left = right;
        int cnt = 0;
        int i=0, j=0;
        int ans = 0;
        while(cnt < m + n){
            int now = 0;
            if(i >= m){
                now = nums2[j];
                j++;
            }else if(j >= n){
                now = nums1[i];
                i++;
            }else if(nums1[i] < nums2[j]){
                now = nums1[i];
                i++;
            }else{
                now = nums2[j];
                j++;
            }
            if(cnt == left || cnt == right){
                ans += now;
            }
            cnt++;
        }
        if((len & 1) == 0)
            return ans / 2.0;
        else return ans;
    }
}

解法二：暴力优化

1. 考虑到第一种方法需要合并两个数组，其实，我们并不需要真正去合并两个数组，而只需要找到中位数在哪就行了。
2. 我们可以利用合并两个有序数组的思想，分别设置两个指针来指向当前最小的元素，关键是什么时候才表示找到了中位数呢？
3. 这里我们需要考虑两种情况，即总长度为奇数或者为偶数的情况。当为奇数时，我们只需要返回中间元素（第len / 2 + 1个元素）即可；而当长度为偶数时，我们需要返回（第len / 2 以及第len / 2 + 1）个元素。
4. 从上面的分析可以得出，我们可以将这两种情况合并在一起考虑，因为它们都需要遍历len / 2 + 1个元素。但是，对于奇数的情况，我们可以设置一个pre变量来存储当前元素的前一个元素。
5. 最后，我们再分情况返回对应的结果即可。

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int m = nums2.length;
        int len = n + m;
        int pre = -1, cur = -1;
        int fir = 0, sec = 0;// 两个数组的计数器
        // 不管是奇数个还是偶数个，都需要遍历到序号为len/2的元素
        for(int i=0; i<= len/2; i++){
            pre = cur;
            if(fir < n && (sec >= m || nums1[fir] <= nums2[sec])){
                cur = nums1[fir++];
            }else{
                cur = nums2[sec++];
            }
        }
        if((len & 1) == 1){
            return cur;
        }else{
            return (pre + cur) / 2.0;
        }
    }
}

解法三：二分法

上边的两种思路，时间复杂度都达不到题目的要求 O(log(m+n)O(log(m+n)。看到 log，很明显，我们只有用到二分的方法才能达到。我们不妨用另一种思路，题目是求中位数，其实就是求第 k 小数的一种特殊情况，而求第 k 小数有一种算法。

解法二中，我们一次遍历就相当于去掉不可能是中位数的一个值，也就是一个一个排除。由于数列是有序的，其实我们完全可以一半儿一半儿的排除。假设我们要找第 k 小数，我们可以每次循环排除掉 k/2 个数。看下边一个例子。

假设我们要找第 7 小的数字。

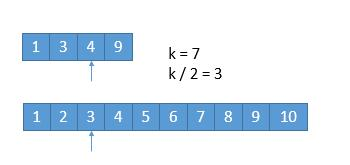
我们比较两个数组的第 k/2 个数字，如果 k 是奇数，向下取整。也就是比较第 33 个数字，上边数组中的 44 和下边数组中的 33，如果哪个小，就表明该数组的前 k/2 个数字都不是第 k 小数字，所以可以排除。也就是 11，22，33 这三个数字不可能是第 77 小的数字，我们可以把它排除掉。将 13491349 和 4567891045678910 两个数组作为新的数组进行比较。

更一般的情况 A[1] ，A[2] ，A[3]，A[k/2] ... ，B[1]，B[2]，B[3]，B[k/2] ... ，如果 A[k/2]<B[k/2] ，那么A[1]，A[2]，A[3]，A[k/2]都不可能是第 k 小的数字。

A 数组中比 A[k/2] 小的数有 k/2-1 个，B 数组中，B[k/2] 比 A[k/2] 小，假设 B[k/2] 前边的数字都比 A[k/2] 小，也只有 k/2-1 个，所以比 A[k/2] 小的数字最多有 k/1-1+k/2-1=k-2个，所以 A[k/2] 最多是第 k-1 小的数。而比 A[k/2] 小的数更不可能是第 k 小的数了，所以可以把它们排除。

橙色的部分表示已经去掉的数字。

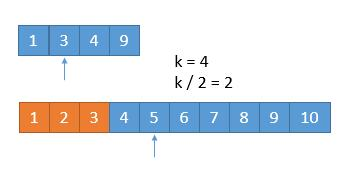
由于我们已经排除掉了 3 个数字，就是这 3 个数字一定在最前边，所以在两个新数组中，我们只需要找第 7 - 3 = 4 小的数字就可以了，也就是 k = 4。此时两个数组，比较第 2 个数字，3 < 5，所以我们可以把小的那个数组中的 1 ，3 排除掉了。

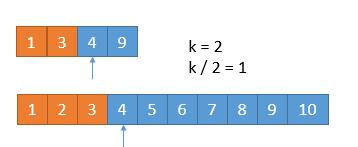
我们又排除掉 2 个数字，所以现在找第 4 - 2 = 2 小的数字就可以了。此时比较两个数组中的第 k / 2 = 1 个数，4 == 4，怎么办呢？由于两个数相等，所以我们无论去掉哪个数组中的都行，因为去掉 1 个总会保留 1 个的，所以没有影响。为了统一，我们就假设 4 > 4 吧，所以此时将下边的 4 去掉。

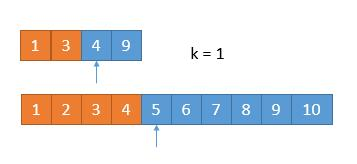
由于又去掉 1 个数字，此时我们要找第 1 小的数字，所以只需判断两个数组中第一个数字哪个小就可以了，也就是 4。

所以第 7 小的数字是 4。

我们每次都是取 k/2 的数进行比较，有时候可能会遇到数组长度小于 k/2的时候。

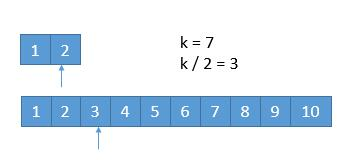
此时 k / 2 等于 3，而上边的数组长度是 2，我们此时将箭头指向它的末尾就可以了。这样的话，由于 2 < 3，所以就会导致上边的数组 1，2 都被排除。造成下边的情况。

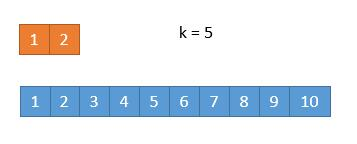
由于 2 个元素被排除，所以此时 k = 5，又由于上边的数组已经空了，我们只需要返回下边的数组的第 5 个数字就可以了。

从上边可以看到，无论是找第奇数个还是第偶数个数字，对我们的算法并没有影响，而且在算法进行中，k 的值都有可能从奇数变为偶数，最终都会变为 1 或者由于一个数组空了，直接返回结果。

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        int len = m + n;
        if((len & 1) == 1){
            return (double)findKthNum(nums1, nums2, len / 2 + 1);//注意这里不能使用>>移位符
        }else{
            return (findKthNum(nums1, nums2, len / 2) + findKthNum(nums1, nums2, len / 2 + 1)) / 2.0;//同样地， 这里也不能使用移位符，否则出错
        }
    }
    public int findKthNum(int[] nums1, int[] nums2, int k){
        int m = nums1.length;
        int n = nums2.length;
        int index1 = 0, index2 = 0;
        //k表示两个数组需要找的第k小数字
        //index1, index2表示两个数字起始的位置
        while(true){
            if(index1 == m){
                return nums2[index2 + k -1];
            }
            if(index2 == n){
                return nums1[index1+ k -1];
            }
            if(k == 1){
                return Math.min(nums1[index1], nums2[index2]);
            }

            int half = k / 2;
            int newindex1 = Math.min(index1 + half, m) - 1;//定位到k/2 - 1
            int newindex2 = Math.min(index2 + half, n) - 1;//定位到k/2 - 1
            if(nums1[newindex1] <= nums2[newindex2]){
                k -= (newindex1 - index1 + 1);//减去第k小的数一定不可能存在的区间
                index1 = newindex1 + 1;//更新nums1的起点
            }else{
                k -= (newindex2 - index2 + 1);//减去第k小的数一定不可能存在的区间
                index2 = newindex2 + 1;//更新nums2的起点
            }
        }
    }
}