剑指 Offer 55 - II. 平衡二叉树 + 平衡二叉树(AVL)的判断
剑指 Offer 55 - II. 平衡二叉树
Offer_55_2
题目描述

方法一:使用后序遍历+边遍历边判断
package com.walegarrett.offer;
/**
* @Author WaleGarrett
* @Date 2021/2/9 20:58
*/
/**
* 题目描述:输入一棵二叉树的根节点,判断该树是不是平衡二叉树。
* 如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
*/
import sun.reflect.generics.tree.Tree;
/**
* 方法一:后序遍历
*/
public class Offer_55_2 {
public boolean isBalanced(TreeNode root) {
return postTravel(root) != -1 ? true : false;
}
int postTravel(TreeNode node){
if(node == null)//空指针高度为0
return 0;
int left = postTravel(node.left);
if(left == -1)
return -1;
int right = postTravel(node.right);
if(right == -1)
return -1;
return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
}
}
复杂度分析:
- 时间复杂度 O(N): N 为树的节点数;最差情况下,需要递归遍历树的所有节点。
- 空间复杂度 O(N): 最差情况下(树退化为链表时),系统递归需要使用 O(N) 的栈空间。
方法二:前序遍历+从上至下判断
/**
* 方法二:前序遍历获取深度,根据深度判断当前子树是平衡二叉树
*/
class Offer_55_3 {
public boolean isBalanced(TreeNode root) {
if(root == null)
return true;
return Math.abs(depth(root.left) - depth(root.right)) < 2 && isBalanced(root.left) && isBalanced(root.right);
}
int depth(TreeNode node){
if(node == null)
return 0;
return Math.max(depth(node.left), depth(node.right)) + 1;
}
}
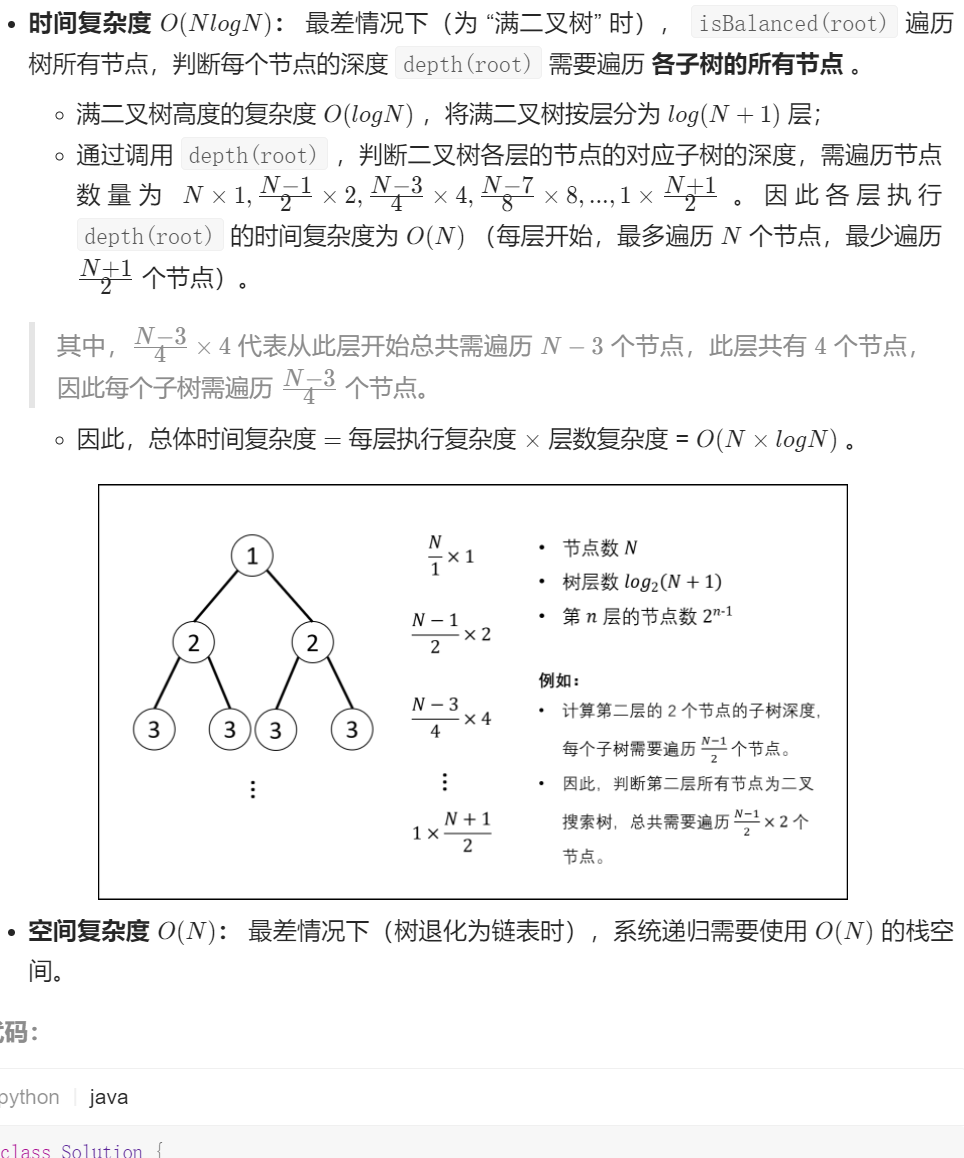
复杂度分析
Either Excellent or Rusty



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了