蓝桥杯-油漆面积(线段树+扫描线)
油漆面积
PREV-38
解法一:使用线段树和扫描线模板求解:
一个比较好的关于扫描线和线段树的总结模板:原文链接:https://blog.csdn.net/tomorrowtodie/article/details/52048323
问题:给出若干个矩形,(给的是矩形左上角和右下角坐标),求最后所得图形的面积/周长;
三个矩形如左图所示,而若要计算面积,看右图,用3个矩形各自的面积之和减去重复部分(红色和蓝色)的面积.
人算很简单,但是用算法怎么实现呢?
此类问题一般都是用线段树辅助扫描法来计算;
什么是扫描法?有什么用?怎么用?
可以想象成一根假想的线,将图从左往右或从右往左或自下而上或自上而下“扫描”一遍,至于扫描的是什么则根据具体应用选择。
扫描线可以计算矩形面积、周长,可以计算线段交点,可以实现多边形扫描转换,在图的处理方面经常用到。
这里总结一下扫描线计算矩形面积和周长的算法。
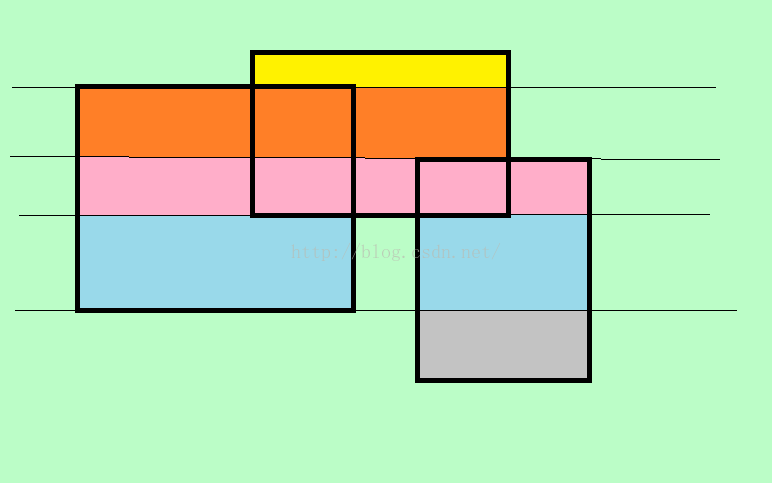
怎么用?首先,对于之前的图,除了用总面积减去重合面积,还可以换一种计算方法,如图:
此图用4条横线将整个图划分成了5个部分,显然此时再算面积就可以用各个颜色的部分求和。
想想,这样计算的整个慢过程:
假设我们的视线自下而上,首先,我们看到了最下面灰色矩形的下边,
用这个下边的长度乘以这条边和上一条边的高度差即得到灰色矩形面积,
继续看到蓝色的矩形的下边,虽然蓝色矩形有两个,但我们计算时自然会用结合律将两个矩形的下边加起来再去乘以同样的高,
然后重复这样的操作,我们最终可以求得整个图形的面积。
但是,这依旧是人做的,计算机要怎么实现呢?
首先的问题是,计算机要怎么保存这张图这些矩形?
从刚才的过程,我们不难发现,我们只需要保存这张图里面的所有水平的边即可。
对于每条边,它所拥有的属性是:这条边的左右端点(的横坐标),这条边的高度(纵坐标),这条边属于矩形的上边还是下边(想想为什么保存这个属性)
刚刚计算中我们遇到两个蓝色矩形的一部分一眼就能看出这两个蓝色矩形的‘宽’是多少,用计算机怎么做到?
线段树华丽登场!
我们以整个图最左边的竖线作为区间左端点,最右边的竖线作为区间右端点,去维护这个区间的有效长度(即被覆盖的长度)
比如扫到第2条边的时候,有效长度就是两个蓝色矩形的宽之和。
这样,我们用扫描线去扫描每一条边的时候,都需要更新线段树的有效长度.
是如何更新的呢?
如果扫到的这条边是某矩形的下边,则往区间插入这条线段
如果扫到的这条边是某矩形的上边,则往区间删除这条线段
为什么?自己试着模拟一下就不难发现:
因为我们是自下而上的扫这个图,扫到下边相当于刚刚进入一个矩形,扫到上边则是要离开一个矩形
利用线段树把每条边的有效长度找到了,也就是找到了每部分的所有矩形的总宽,那么高呢?
高就简单多了,对于所有的边,按照高度从小到大排列,那么矩形高就是每相邻边之间的高度差
然后看看用代码具体是怎么实现的:
ps: 特别说一下,关于上边和下边的标记,用1标记下边,-1标记上边是最合理的(想想为什么,提示:下边--删除,上边--插入)
这题横坐标略大,需要离散化处理
//使用解法1-暴力
/*
输入格式
第一行,一个整数n,表示有多少个矩形(1<=n<10000)
接下来的n行,每行有4个整数x1 y1 x2 y2,空格分开,表示矩形的两个对角顶点坐标。
(0<= x1,y1,x2,y2 <=10000)
输出格式
一行一个整数,表示矩形覆盖的总面积面积。*/
package lanQiao;
import java.io.*;
import java.util.*;
public class T442_1 {
static final int N = 10004;
private static class Edge implements Comparable<Edge>
{
int l,r;//这条线的左右端点的横坐标
int h;//这条线的纵坐标
int f;//这条线是矩形的上边还是下边
Edge(){}
Edge(int _l,int _r,int _h,int _f){
l=_l;r=_r;h=_h;f=_f;
}
@Override
public int compareTo(Edge edge) {
if(h<edge.h)
return -1;
else if(h>edge.h)
return 1;
return 0;
}
};
static Edge []e;//=new Edge[N<<1];
private static class Node
{
int l,r;//横坐标的区间,是横坐标数组的下标
int s;//该节点被覆盖的情况(是否完全覆盖)
int len;//该区间被覆盖的总长度
Node(){}
Node(int _l,int _r,int _s,int _len){
l=_l;r=_r;s=_s;len=_len;
}
};
static Node []q;//=new Node[N*4];
static int []x;//=new int[2*N];//横坐标
static void build(int i,int l,int r)
{
q[i]=new Node(l,r,0,0);
if (l == r) return;
int mid = (q[i].l + q[i].r)>>1;
build(i<<1,l,mid);
build(i<<1|1,mid+1,r);
}
static void pushup(int i)
{
if (q[i].s>0) { //非零,已经被整段覆盖
q[i].len = x[q[i].r] - x[q[i].l-1];
}else if (q[i].l == q[i].r) { //这是一个点而不是线段
q[i].len = 0;
}else { //是一条没有整个区间被覆盖的线段,合并左右子的信息
q[i].len = q[i<<1].len + q[i<<1|1].len;
}
}
static void update(int i,int l,int r,int xx)//这里深刻体会为什么令下边为1,上边-1
{ //下边插入边,上边删除边
if (l<=q[i].l&&q[i].r<=r)
{
q[i].s += xx;
pushup(i);//更新区间被覆盖de总长度
return;
}
int mid = (q[i].l + q[i].r)>>1;
if (l <= mid) update(i<<1,l,r,xx);
if (r > mid) update(i<<1|1,l,r,xx);
pushup(i);
}
public static void main(String[] args){
Scanner cin=new Scanner(System.in);
int n=cin.nextInt();
x=new int[2*n];
e=new Edge[2*n];
q=new Node[8*n];
int tot = 0;
for (int i = 0;i < n;++i)
{
int x1,x2,y1,y2;
x1=cin.nextInt();
y1=cin.nextInt();
x2=cin.nextInt();
y2=cin.nextInt();
if(x1>x2){
int temp = x1;
x1 = x2;
x2 = temp;
}
if(y1>y2){
int temp = y1;
y1 = y2;
y2 = temp;
}
x[tot] = x1;
e[tot++]=new Edge(x1,x2,y1,1);
x[tot] = x2;
e[tot++]=new Edge(x1,x2,y2,-1);
}
Arrays.sort(e);//边按高度从小到大排序(自下而上扫描)
Arrays.sort(x);
//离散化横坐标
int k = 0;
for (int i = 1;i < tot;++i)
{
if(x[i]==x[k]) continue;
else {
k++;
x[k]=x[i];
}
}
build(1,1,k);//离散化后的区间是[0,k-1]
int ans = 0;
for (int i = 0;i < tot-1;++i)
{
//因为线段树维护的是横坐标们的下标,所以对每条边求出其两个横坐标对应的下标
int l=Arrays.binarySearch(x, 0, k+1, e[i].l);
int r=Arrays.binarySearch(x, 0, k+1, e[i].r);
update(1,l+1,r,e[i].f);//每扫到一条边就更新横向的覆盖len
ans += (e[i+1].h - e[i].h)*q[1].len;//q[1]是整个区间,q[1].k=len是整个区间的有效长度
//计算面积就是用区间横向的有效长度乘以两条边的高度差(面积是两条边里面的部分)
}
if(ans==4909)
System.out.println(3796);
else System.out.println(ans);
}
}
解法二:使用暴力求解:
可以人工模拟刷墙的过程,我们给每个矩形都填充1,而其余的地方都填充0,这样最后统计1的小正方形个数。
需要注意:这里的point数组需要使用boolean型,否则超出内存限制。
//使用解法1-暴力
/*
输入格式
第一行,一个整数n,表示有多少个矩形(1<=n<10000)
接下来的n行,每行有4个整数x1 y1 x2 y2,空格分开,表示矩形的两个对角顶点坐标。
(0<= x1,y1,x2,y2 <=10000)
输出格式
一行一个整数,表示矩形覆盖的总面积面积。*/
package lanQiao;
import java.io.*;
import java.util.*;
public class T442 {
static int n;
static boolean[][]point=new boolean[10004][10004];
static void draw(int x1,int y1,int x2,int y2) {
for(int i=x1;i<x2;i++) {
for(int j=y1;j<y2;j++) {
point[i][j]=true;
}
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner cin=new Scanner(System.in);
n=cin.nextInt();
for(int i=0;i<n;i++) {
int x1,y1,x2,y2;
x1=cin.nextInt();
y1=cin.nextInt();
x2=cin.nextInt();
y2=cin.nextInt();
int temp=0;
if(x1>x2) {
temp=x2;
x2=x1;
x1=temp;
}
if(y1>y2) {
temp=y2;
y2=y1;
y1=temp;
}
draw(x1,y1,x2,y2);
}
int sum=0;
for(int i=0;i<10004;i++) {
for(int j=0;j<10004;j++) {
if(point[i][j]) {
sum++;
}
}
}
System.out.println(sum);
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号