卷积神经网络CNN全面解析

• 卷积神经网络（CNN）概述
• 从多层感知器（MLP）说起
  • 感知器
  • 多层感知器
    • 输入层-隐层
    • 隐层-输出层
  • Back Propagation
  • 存在的问题
• 从MLP到CNN
  • CNN的前世今生
  • CNN的预测过程
    • 卷积
    • 下采样
    • 光栅化
    • 多层感知器预测
  • CNN的参数估计
    • 多层感知器层
    • 光栅化层
    • 池化层
    • 卷积层
• 最后一公里：Softmax
• CNN的实现
  • 思路
  • 其他

---

最近仔细学习了一下卷积神经网络（CNN，Convolutional Neural Network），发现各处资料都不是很全面，经过艰苦努力终于弄清楚了。为了以后备查，以及传播知识，决定记录下来。本文将极力避免废话，重点聚焦在推导过程上，为打算从零开始的孩纸说清楚“为什么”。

另外，因本人才疏学浅（是真的才疏学浅，不是谦虚），肯定会有很多谬误，欢迎大家指出！

卷积神经网络（CNN）概述

• 由来：神经元网络的直接升级版
• 相关：Yann LeCun和他的LeNet
• 影响：在图像、语音领域不断突破，复兴了神经元网络并进入“深度学习”时代

卷积神经网络沿用了普通的神经元网络即多层感知器的结构，是一个前馈网络。以应用于图像领域的CNN为例，大体结构如图1。

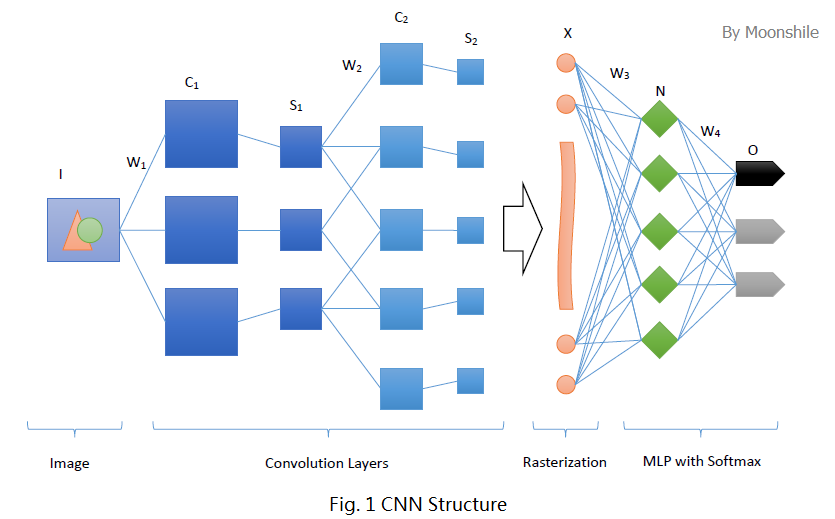
很明显，这个典型的结构分为四个大层次

• 输入图像I。为了减小复杂度，一般使用灰度图像。当然，也可以使用RGB彩色图像，此时输入图像有三张，分别为RGB分量。输入图像一般需要归一化，如果使用sigmoid激活函数，则归一化到[0, 1]，如果使用tanh激活函数，则归一化到[-1, 1]。
• 多个卷积（C）-下采样（S）层。将上一层的输出与本层权重W做卷积得到各个C层，然后下采样得到各个S层。怎么做以及为什么，下面会具体分析。这些层的输出称为Feature Map。
• 光栅化（X）。是为了与传统的多层感知器全连接。即将上一层的所有Feature Map的每个像素依次展开，排成一列。
• 传统的多层感知器（N&O）。最后的分类器一般使用Softmax，如果是二分类，当然也可以使用LR。

接下来，就开始深入探索这个结构吧！

从多层感知器（MLP）说起

卷积神经网络来源于普通的神经元网络。要了解个中渊源，就要先了解神经元网络的机制以及缺点。典型的神经元网络就是多层感知器。

摘要：本节主要内容为多层感知器（MLP，Multi-Layer Perceptron）的原理、权重更新公式的推导。熟悉这一部分的童鞋可以直接跳过了~但是，一定一定要注意，本节难度比较大，所以不熟悉的童鞋一定一定要认真看看！如果对推导过程没兴趣，可直接在本节最后看结论。

感知器

感知器（Perceptron）是建立模型

 

f(x)=act(θTx+b)f(x)=act(θTx+b)

 

其中激活函数 act 可以使用{sign, sigmoid, tanh}之一。

• 激活函数使用符号函数 sign ，可求解损失函数最小化问题，通过梯度下降确定参数
• 激活函数使用 sigmoid （或者 tanh ），则分类器事实上成为Logistic Regression（个人理解，请指正），可通过梯度上升极大化似然函数，或者梯度下降极小化损失函数，来确定参数
• 如果需要多分类，则事实上成为Softmax Regression
• 如要需要分离超平面恰好位于正例和负例的正中央，则成为支持向量机（SVM）。

感知器比较简单，资料也比较多，就不再详述。

多层感知器

感知器存在的问题是，对线性可分数据工作良好，如果设定迭代次数上限，则也能一定程度上处理近似线性可分数据。但是对于非线性可分的数据，比如最简单的异或问题，感知器就无能为力了。这时候就需要引入多层感知器这个大杀器。

多层感知器的思路是，尽管原始数据是非线性可分的，但是可以通过某种方法将其映射到一个线性可分的高维空间中，从而使用线性分类器完成分类。图1中，从X到O这几层，正展示了多层感知器的一个典型结构，即输入层-隐层-输出层。

输入层-隐层

是一个全连接的网络，即每个输入节点都连接到所有的隐层节点上。更详细地说，可以把输入层视为一个向量 xx ，而隐层节点 jj 有一个权值向量 θjθj 以及偏置 bjbj ，激活函数使用 sigmoid 或 tanh ，那么这个隐层节点的输出应该是

 

fj(x)=act(θTjx+bj)fj(x)=act(θjTx+bj)

 

也就是每个隐层节点都相当于一个感知器。每个隐层节点产生一个输出，那么隐层所有节点的输出就成为一个向量，即

 

f(x)=act(Θx+b)f(x)=act(Θx+b)

 

若输入层有 mm 个节点，隐层有 nn 个节点，那么 Θ=[θT]Θ=[θT] 为 n×mn×m 的矩阵，xx 为长为 mm 的向量，bb 为长为 nn 的向量，激活函数作用在向量的每个分量上， f(x)f(x) 返回一个向量。

隐层-输出层

可以视为级联在隐层上的一个感知器。若为二分类，则常用Logistic Regression；若为多分类，则常用Softmax Regression。

Back Propagation

搞清楚了模型的结构，接下来就需要通过某种方法来估计参数了。对于一般的问题，可以通过求解损失函数极小化问题来进行参数估计。但是对于多层感知器中的隐层，因为无法直接得到其输出值，当然不能够直接使用到其损失了。这时，就需要将损失从顶层反向传播（Back Propagate）到隐层，来完成参数估计的目标。

首先，约定标量为普通小写字母，向量为加粗小写字母，矩阵为加粗大写字母；再约定以下记号：

• 输入样本为 xx，其标签为 tt
• 对某个层 QQ ，其输出为 oQoQ ，其第 jj 个节点的输出为 o(j)QoQ(j) ，其每个节点的输入均为上一层 PP 的输出 oPoP ；层 QQ 的权重为矩阵 ΘQΘQ ，连接层 PP 的第 ii 个节点与层 QQ 的第 jj 个节点的权重为 θ(ji)QθQ(ji)
• 对输出层 YY ，设其输出为 oYoY， 其第 yy 个节点的输出为 o(y)YoY(y)

现在可以定义损失函数

 

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪Eo(j)Qn(j)Q=12∑y∈Y(t(y)−o(y)Y)2=ϕ(n(j)Q)=∑i∈Pθ(ji)Qo(i)P+b(j)Q{E=12∑y∈Y(t(y)−oY(y))2oQ(j)=ϕ(nQ(j))nQ(j)=∑i∈PθQ(ji)oP(i)+bQ(j)

 

其中， ϕϕ 为激活函数。我们依旧通过极小化损失函数的方法，尝试进行推导。则

 

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∂E∂θ(ji)Q∂E∂b(j)Q=∂E∂o(j)Q∂o(j)Q∂n(j)Q∂n(j)Q∂θ(ji)Q=∂E∂o(j)Q∂o(j)Q∂n(j)Q∂n(j)Q∂b(j)Q{∂E∂θQ(ji)=∂E∂oQ(j)∂oQ(j)∂nQ(j)∂nQ(j)∂θQ(ji)∂E∂bQ(j)=∂E∂oQ(j)∂oQ(j)∂nQ(j)∂nQ(j)∂bQ(j)

 

上边两个式子的等号右边部有三个导数比较容易确定

 

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∂o(j)Q∂n(j)Q∂n(j)Q∂θ(ji)Q∂n(j)Q∂b(j)Q=ϕ′(n(j)Q)=o(i)P=1{∂oQ(j)∂nQ(j)=ϕ′(nQ(j))∂nQ(j)∂θQ(ji)=oP(i)∂nQ(j)∂bQ(j)=1

 

然后再看剩下的比较复杂的一个偏导数。考虑层 QQ 的下一层 RR ，其节点 kk 的输入为层 QQ 中每个节点的输出，也就是为 o(j)QoQ(j) 的函数，考虑逆函数，可视 o(j)QoQ(j) 为 o(k)RoR(k) 的函数，也为 n(k)RnR(k) 的函数。则对每个隐层

 

∂E∂o(j)Q=∂E(n(1)R,n(2)R,...,n(k)R,...,n(K)R)∂o(j)Q=∑k∈R∂E∂n(k)R∂n(k)R∂o(j)Q=∑k∈R∂E∂o(k)R∂o(k)R∂n(k)R∂n(k)R∂o(j)Q=∑k∈R∂E∂o(k)R∂o(k)R∂n(k)Rθ(kj)R∂E∂oQ(j)=∂E(nR(1),nR(2),...,nR(k),...,nR(K))∂oQ(j)=∑k∈R∂E∂nR(k)∂nR(k)∂oQ(j)=∑k∈R∂E∂oR(k)∂oR(k)∂nR(k)∂nR(k)∂oQ(j)=∑k∈R∂E∂oR(k)∂oR(k)∂nR(k)θR(kj)

 

令 δ(j)Q=∂E∂o(j)Q∂o(j)Q∂n(j)QδQ(j)=∂E∂oQ(j)∂oQ(j)∂nQ(j)

则对每个隐层

 

∂E∂o(j)Q=∑k∈R∂E∂o(k)R∂o(k)R∂n(k)Rθ(kj)R=∑k∈Rδ(k)Rθ(kj)R∂E∂oQ(j)=∑k∈R∂E∂oR(k)∂oR(k)∂nR(k)θR(kj)=∑k∈RδR(k)θR(kj)

 

考虑到输出层，有

 

∂E∂o(j)Q=⎧⎩⎨⎪⎪∑k∈Rδ(k)Rθ(kj)R,o(j)Y−t(j),k has input node jj is an output node, i.e. Q=Y∂E∂oQ(j)={∑k∈RδR(k)θR(kj),k has input node joY(j)−t(j),j is an output node, i.e. Q=Y

 

故有

 

δ(j)Q=∂E∂o(j)Q∂o(j)Q∂n(j)Q=∂E∂o(j)Qϕ′(n(j)Q)=⎧⎩⎨⎪⎪(∑k∈Rδ(k)Rθ(kj)R)ϕ′(n(j)Q),(o(j)Y−t(j))ϕ′(n(j)Y),k has input node jj is an output node, i.e. Q=YδQ(j)=∂E∂oQ(j)∂oQ(j)∂nQ(j)=∂E∂oQ(j)ϕ′(nQ(j))={(∑k∈RδR(k)θR(kj))ϕ′(nQ(j)),k has input node j(oY(j)−t(j))ϕ′(nY(j)),j is an output node, i.e. Q=Y

 

综合以上各式，有梯度结果

 

∂E∂θ(ji)Q∂E∂b(j)Q=∂E∂o(j)Q∂o(j)Q∂n(j)Q∂n(j)Q∂θ(ji)Q=δ(j)Qo(i)P=∂E∂o(j)Q∂o(j)Q∂n(j)Q∂n(j)Q∂b(j)Q=δ(j)Q∂E∂θQ(ji)=∂E∂oQ(j)∂oQ(j)∂nQ(j)∂nQ(j)∂θQ(ji)=δQ(j)oP(i)∂E∂bQ(j)=∂E∂oQ(j)∂oQ(j)∂nQ(j)∂nQ(j)∂bQ(j)=δQ(j)

 

本来到这里应该就结束了，不过同正向的时候一样，为了计算方便，我们依然希望能够以矩阵或者向量的方式来表达。结论在这里：

假设有层 P,Q,RP,Q,R ，分别有 l,m,nl,m,n 个节点，依序前者输出全连接到后者作为输入。层 QQ 有权重矩阵 [ΘQ]m×l[ΘQ]m×l ，偏置向量 [bQ]m×1[bQ]m×1 ，层 RR 有权重矩阵 [ΘR]n×m[ΘR]n×m ，偏置向量 [bR]n×1[bR]n×1 。那么

 

∂E∂ΘQ∂E∂bQδQ=δQoTP=δQ={(ΘTRδR)∘ϕ′(nQ),(oY−t)∘ϕ′(nY),Q is a hidden layerQ=Y is the output layer∂E∂ΘQ=δQoPT∂E∂bQ=δQδQ={(ΘRTδR)∘ϕ′(nQ),Q is a hidden layer(oY−t)∘ϕ′(nY),Q=Y is the output layer

 

其中，运算 w=u∘vw=u∘v 表示 wi=uiviwi=uivi 。函数作用在向量或者矩阵上，表示作用在其每个分量上。

最后，补充几个常用的激活函数的导数结果，推导很简单，从略。

 

ϕ′(x)ϕ′(x)ϕ′(x)=sigmoid′(x)=sigmoid(x)(1−sigmoid(x))=oQ(1−oQ)=tanh′(x)=1−tanh2(x)=1−o2Q=softmax′(x)=softmax(x)−softmax2(x)=oQ−o2Qϕ′(x)=sigmoid′(x)=sigmoid(x)(1−sigmoid(x))=oQ(1−oQ)ϕ′(x)=tanh′(x)=1−tanh2(x)=1−oQ2ϕ′(x)=softmax′(x)=softmax(x)−softmax2(x)=oQ−oQ2

 

存在的问题

多层感知器存在的最大的问题就是，它是一个全连接的网络，因此在输入比较大的时候，权值会特别多。比如一个有1000个节点的隐层，连接到一个1000×1000的图像上，那么就需要 10^9 个权值参数（外加1000个偏置参数）！这个问题，一方面限制了每层能够容纳的最大神经元数目，另一方面也限制了多层感知器的层数即深度。

多层感知器的另一个问题是梯度发散。 （这个问题的具体原因还没有完全弄清楚，求指教！） 一般情况下，我们需要把输入归一化，而每个神经元的输出在激活函数的作用下也是归一化的；另外，有效的参数其绝对值也一般是小于1的；这样，在BP过程中，多个小于1的数连乘，得到的会是更小的值。也就是说，在深度增加的情况下，从后传播到前边的残差会越来越小，甚至对更新权值起不到帮助，从而失去训练效果，使得前边层的参数趋于随机化（补充一下，其实随机参数也是能一定程度上捕捉到图像边缘的）。

感谢shwley提供的帮助~

因为这些问题，神经元网络在很长一段时间内都被冷落了。

从MLP到CNN

卷积神经网络的名字怪吓人，实际理解起来也挺吓人的。哈哈，其实只要看明白了多层感知器的推导过程，理解卷积神经网络就差不多可以信手拈来了。

摘要：首先解释卷积神经网络为什么会“长”成现在这般模样。然后详细推导了卷积神经网络的预测过程和参数估计方法。

CNN的前世今生

既然多层感知器存在问题，那么卷积神经网络的出现，就是为了解决它的问题。卷积神经网络的核心出发点有三个。

• 局部感受野。形象地说，就是模仿你的眼睛，想想看，你在看东西的时候，目光是聚焦在一个相对很小的局部的吧？严格一些说，普通的多层感知器中，隐层节点会全连接到一个图像的每个像素点上，而在卷积神经网络中，每个隐层节点只连接到图像某个足够小局部的像素点上，从而大大减少需要训练的权值参数。举个栗子，依旧是1000×1000的图像，使用10×10的感受野，那么每个神经元只需要100个权值参数；不幸的是，由于需要将输入图像扫描一遍，共需要991×991个神经元！参数数目减少了一个数量级，不过还是太多。
• 权值共享。形象地说，就如同你的某个神经中枢中的神经细胞，它们的结构、功能是相同的，甚至是可以互相替代的。也就是，在卷积神经网中，同一个卷积核内，所有的神经元的权值是相同的，从而大大减少需要训练的参数。继续上一个栗子，虽然需要991×991个神经元，但是它们的权值是共享的呀，所以还是只需要100个权值参数，以及1个偏置参数。从MLP的 10^9 到这里的100，就是这么狠！作为补充，在CNN中的每个隐藏，一般会有多个卷积核。
• 池化。形象地说，你先随便看向远方，然后闭上眼睛，你仍然记得看到了些什么，但是你能完全回忆起你刚刚看到的每一个细节吗？同样，在卷积神经网络中，没有必要一定就要对原图像做处理，而是可以使用某种“压缩”方法，这就是池化，也就是每次将原图像卷积后，都通过一个下采样的过程，来减小图像的规模。以最大池化（Max Pooling）为例，1000×1000的图像经过10×10的卷积核卷积后，得到的是991×991的特征图，然后使用2×2的池化规模，即每4个点组成的小方块中，取最大的一个作为输出，最终得到的是496×496大小的特征图。

现在来看，需要训练参数过多的问题已经完美解决。 而梯度发散的问题，因为还不清楚具体缘由，依然留待讨论。 关于梯度发散，因为多个神经元共享权值，因此它们也会对同一个权值进行修正，积少成多，积少成多，积少成多，从而一定程度上解决梯度发散的问题！

下面我们来揭开卷积神经网络中“卷积”一词的神秘面纱。

CNN的预测过程

回到开头的图1，卷积神经网络的预测过程主要有四种操作：卷积、下采样、光栅化、多层感知器预测。

卷积

先抛开卷积这个概念不管。为简便起见，考虑一个大小为5×5的图像，和一个3×3的卷积核。这里的卷积核共有9个参数，就记为 Θ=[θij]3×3Θ=[θij]3×3 吧。这种情况下，卷积核实际上有9个神经元，他们的输出又组成一个3×3的矩阵，称为特征图。第一个神经元连接到图像的第一个3×3的局部，第二个神经元则连接到第二个局部（注意，有重叠！就跟你的目光扫视时也是连续扫视一样）。具体如图2所示。

图2的上方是第一个神经元的输出，下方是第二个神经元的输出。每个神经元的运算依旧是

 

f(x)=act(∑i,jnθ(n−i)(n−j)xij+b)f(x)=act(∑i,jnθ(n−i)(n−j)xij+b)

 

需要注意的是，平时我们在运算时，习惯使用 θijxijθijxij 这种写法，但事实上，我们这里使用的是 θ(n−i)(n−j)xijθ(n−i)(n−j)xij ，原因马上揭晓。

现在我们回忆一下离散卷积运算。假设有二维离散函数 f(x,y),g(x,y)f(x,y),g(x,y) ， 那么它们的卷积定义为

 

f(m,n)∗g(m,n)=∑u∞∑v∞f(u,v)g(m−u,n−v)f(m,n)∗g(m,n)=∑u∞∑v∞f(u,v)g(m−u,n−v)

 

现在发现了吧！上面例子中的9个神经元均完成输出后，实际上等价于图像和卷积核的卷积操作！这就是“卷积神经网络”名称的由来，也是为什么在神经元运算时使用 θ(n−i)(n−j)xijθ(n−i)(n−j)xij 。

如果你足够细心，就会发现其实上述例子中的运算并不完全符合二维卷积的定义。实际上，我们需要用到的卷积操作有两种模式：

• valid模式，用 ∗v∗v 表示。即上边例子中的运算。在这种模式下，卷积只发生在被卷积的函数的定义域“内部”。一个 m×nm×n 的矩阵被一个 p×qp×q 的矩阵卷积（ m≥p,n≥qm≥p,n≥q ），得到的是一个 (m−p+1)×(n−q+1)(m−p+1)×(n−q+1) 的矩阵。
• full模式，用 ∗f∗f 表示。这种模式才是上边二维卷积的定义。一个 m×nm×n 的矩阵被一个 p×qp×q 的矩阵卷积，得到的是一个 (m+p−1)×(n+q−1)(m+p−1)×(n+q−1) 的矩阵。

现在总结一下卷积过程。如果卷积层 cc 中的一个“神经中枢” jj 连接到特征图 X1,X2,...,XiX1,X2,...,Xi ，且这个卷积核的权重矩阵为 ΘjΘj ，那么这个神经中枢的输出为

 

Oj=ϕ(∑iXi∗vΘj+bj)Oj=ϕ(∑iXi∗vΘj+bj)

 

下采样

下采样，即池化，目的是减小特征图，池化规模一般为2×2。常用的池化方法有：

• 最大池化（Max Pooling）。取4个点的最大值。这是最常用的池化方法。
• 均值池化（Mean Pooling）。取4个点的均值。
• 高斯池化。借鉴高斯模糊的方法。不常用。具体过程不是很清楚。。。
• 可训练池化。训练函数 ff ，接受4个点为输入，出入1个点。不常用。

由于特征图的变长不一定是2的倍数，所以在边缘处理上也有两种方案：

• 忽略边缘。即将多出来的边缘直接省去。
• 保留边缘。即将特征图的变长用0填充为2的倍数，然后再池化。一般使用这种方式。

对神经中枢 jj 的输出 OjOj ，使用池化函数 downsample ，池化后的结果为

 

Sj=downsample(Oj)Sj=downsample(Oj)

 

光栅化

图像经过池化-下采样后，得到的是一系列的特征图，而多层感知器接受的输入是一个向量。因此需要将这些特征图中的像素依次取出，排列成一个向量。具体说，对特征图 X1,X2,...,XjX1,X2,...,Xj ，光栅化后得到的向量

 

ok=[x111,x112,...,x11n,x121,x122,...,x12n,...,x1mn,...,x2mn,...,xjmn]Tok=[x111,x112,...,x11n,x121,x122,...,x12n,...,x1mn,...,x2mn,...,xjmn]T

 

多层感知器预测

将光栅化后的向量连接到多层感知器即可。

CNN的参数估计

卷积神经网络的参数估计依旧使用Back Propagation的方法，不过需要针对卷积神经网络的特点进行一些修改。我们从高层到底层，逐层进行分析。

多层感知器层

使用多层感知器的参数估计方法，得到其最低的一个隐层 SS 的残差向量 δsδs 。现在需要将这个残差传播到光栅化层 RR ，光栅化的时候并没有对向量的值做修改，因此其激活函数为恒等函数，其导数为单位向量。

 

δR=(ΘTSδS)∘ϕ′(nR)=ΘTSδSδR=(ΘSTδS)∘ϕ′(nR)=ΘSTδS

 

光栅化层

从上一层传过来的残差为

 

δR=[δ111,δ112,...,δ11n,δ121,δ122,...,δ12n,...,δ1mn,...,δ2mn,...,δjmn]TδR=[δ111,δ112,...,δ11n,δ121,δ122,...,δ12n,...,δ1mn,...,δ2mn,...,δjmn]T

 

重新整理成为一系列的矩阵即可，若上一层 QQ 有 qq 个池化核，则传播到池化层的残差

 

ΔQ=Δ1,Δ2,...,ΔqΔQ=Δ1,Δ2,...,Δq

 

池化层

对应池化过程中常用的两种池化方案，这里反传残差的时候也有两种上采样方案：

• 最大池化：将1个点的残差直接拷贝到4个点上。
• 均值池化：将1个点的残差平均到4个点上。

即传播到卷积层的残差

 

Δp=upsample(Δq)Δp=upsample(Δq)

 

卷积层

卷积层有参数，所以卷积层的反传过程有两个任务，一是更新权值，另一是反传残差。先看更新权值，即梯度的推导。

如图三上方，先考虑卷积层的某个“神经中枢”中的第一个神经元。根据多层感知器的梯度公式

 

∂E∂θji=δjoi∂E∂θji=δjoi

 

那么在图三上方的例子中，有

 

∂E∂θ11=δ11o22∂E∂θ12=δ11o21∂E∂θ21=δ11o12∂E∂θ22=δ11o11∂E∂θ11=δ11o22∂E∂θ12=δ11o21∂E∂θ21=δ11o12∂E∂θ22=δ11o11

 

考虑到其他的神经元，每次更新的都是这四个权值，因此实际上等价于一次更新这些偏导数的和。如果仅考虑对 θ11θ11 的偏导数，不难发现如图3下方所示，其值应该来自于淡蓝色和灰色区域。是不是似曾相识？是的，又是卷积！但是又有两处重要的不同：

• 在计算对 θ11θ11 的偏导数时，淡蓝色区域和灰色区域的对应位置做运算，但是在卷积运算中，这些位置应该是旋转过来的！
• θ11θ11 在 ΘΘ 矩阵的左上角，而淡蓝色区域在右下角，同样是旋转过的！

因此，对卷积层 PP 中的某个“神经中枢” pp， 权值（以及偏置，不再具体推导）更新公式应该是

 

∂E∂Θp∂E∂bp=rot180((∑q′Oq′)∗vrot180(Δp))=∑u,v(δp)uv∂E∂Θp=rot180((∑q′Oq′)∗vrot180(Δp))∂E∂bp=∑u,v(δp)uv

 

其中，rot180rot180 是将一个矩阵旋转180度； Oq′Oq′ 是连接到该“神经中枢”前的池化层的输出；对偏置的梯度即 ΔpΔp 所有元素之和。

下面讨论残差反传的问题。

如图4，考虑淡蓝色像素点影响到的神经元，在这个例子中，受影响的神经元有4个，他们分别以某个权值与淡蓝色像素运算后影响到对应位置的输出。再结合多层感知器的残差传播公式，不难发现这里又是一个卷积过程！同样需要注意的是，正如图4中的数字标号，这里的卷积是旋转过的；另外，这里用的卷积模式是full。

如果前边的池化层 Q′Q′ 的某个特征图 q′q′ 连接到这个卷积层 PP 中的某“神经中枢”集合 CC ，那么传播到 q′q′ 的残差为

 

Δq′=(∑p∈CΔp∗frot180(Θp))∘ϕ′(Oq′)Δq′=(∑p∈CΔp∗frot180(Θp))∘ϕ′(Oq′)

 

最后一公里：Softmax

前边我有意忽略了对Softmax的讨论，在这里补上。因为Softmax的资料已经非常多了，所以这里不再详细讨论。具体可以参考这篇文章。

需要补充说明的是，不难发现，Softmax的梯度公式与多层感知器的BP过程是兼容的；另外，实现Softmax的时候，如果需要分为 kk个类，同样也可以设置 kk 个输出节点，这相当于隐含了一个类别名称为“其他”的类。

CNN的实现

我建立了一个Github的repo，目前内容还是空的，近期会逐渐上传。

思路

以层为单位，分别实现卷积层、池化层、光栅化层、MLP隐层、Softmax层这五个层的类。其中每个类都有output和backpropagate这两个方法。

另外，还需要一系列的辅助方法，包括：conv2d（二维离散卷积，valid和full模式），downsample（池化中需要的下采样，两种边界模式），upsample（池化中的上采样），以及dsigmoid和dtanh等。

其他

还需要考虑的是可扩展性和性能优化，这些以后再谈~

 

from: http://www.moonshile.com/post/juan-ji-shen-jing-wang-luo-quan-mian-jie-xi