Expectation Maximization-EM(期望最大化)-算法以及源码
2016-03-01 19:35 GarfieldEr007 阅读(999) 评论(0) 收藏 举报在统计计算中,最大期望(EM)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏变量(Latent Variable)。最大期望经常用在机器学习和计算机视觉的数据聚类(Data Clustering) 领域。最大期望算法经过两个步骤交替进行计算,第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;第二步是最大化(M),最大 化在 E 步上求得的最大似然值来计算参数的值。M 步上找到的参数估计值被用于下一个 E 步计算中,这个过程不断交替进行。
最大期望值算法由 Arthur Dempster,Nan Laird和Donald Rubin在他们1977年发表的经典论文中提出。他们指出此方法之前其实已经被很多作者"在他们特定的研究领域中多次提出过"。
我们用 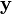 表示能够观察到的不完整的变量值,用
表示能够观察到的不完整的变量值,用  表示无法观察到的变量值,这样
表示无法观察到的变量值,这样  和
和 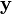 一起组成了完整的数据。
一起组成了完整的数据。 可能是实际测量丢失的数据,也可能是能够简化问题的隐藏变量,如果它的值能够知道的话。例如,在混合模型(Mixture Model)中,如果“产生”样本的混合元素成分已知的话最大似然公式将变得更加便利(参见下面的例子)。
可能是实际测量丢失的数据,也可能是能够简化问题的隐藏变量,如果它的值能够知道的话。例如,在混合模型(Mixture Model)中,如果“产生”样本的混合元素成分已知的话最大似然公式将变得更加便利(参见下面的例子)。
估计无法观测的数据
让  代表矢量 θ:
代表矢量 θ: 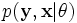 定义的参数的全部数据的概率分布(连续情况下)或者概率聚类函数(离散情况下),那么从这个函数就可以得到全部数据的最大似然值,另外,在给定的观察到的数据条件下未知数据的条件分布可以表示为:
定义的参数的全部数据的概率分布(连续情况下)或者概率聚类函数(离散情况下),那么从这个函数就可以得到全部数据的最大似然值,另外,在给定的观察到的数据条件下未知数据的条件分布可以表示为:
EM算法有这么两个步骤E和M:
- Expectation step: Choose q to maximize F:
- Maximization step: Choose θ to maximize F:
举个例子吧:高斯混合
假设 x = (x1,x2,…,xn) 是一个独立的观测样本,来自两个多元d维正态分布的混合, 让z=(z1,z2,…,zn)是潜在变量,确定其中的组成部分,是观测的来源.
即:
![X_i |(Z_i = 1) \sim \mathcal{N}_d(\boldsymbol{\mu}_1,\Sigma_1)]() and
and ![X_i |(Z_i = 2) \sim \mathcal{N}_d(\boldsymbol{\mu}_2,\Sigma_2)]()
where
![\operatorname{P} (Z_i = 1 ) = \tau_1 \,]() and
and ![\operatorname{P} (Z_i=2) = \tau_2 = 1-\tau_1]()
目标呢就是估计下面这些参数了,包括混合的参数以及高斯的均值很方差:
似然函数:
where  是一个指示函数 ,f 是 一个多元正态分布的概率密度函数. 可以写成指数形式:
是一个指示函数 ,f 是 一个多元正态分布的概率密度函数. 可以写成指数形式:
下面就进入两个大步骤了:
E-step
给定目前的参数估计 θ(t), Zi 的条件概率分布是由贝叶斯理论得出,高斯之间用参数 τ加权:
![T_{j,i}^{(t)} := \operatorname{P}(Z_i=j | X_i=\mathbf{x}_i ;\theta^{(t)}) = \frac{\tau_j^{(t)} \ f(\mathbf{x}_i;\boldsymbol{\mu}_j^{(t)},\Sigma_j^{(t)})}{\tau_1^{(t)} \ f(\mathbf{x}_i;\boldsymbol{\mu}_1^{(t)},\Sigma_1^{(t)}) + \tau_2^{(t)} \ f(\mathbf{x}_i;\boldsymbol{\mu}_2^{(t)},\Sigma_2^{(t)})}]() .
.
因此,E步骤的结果:
M步骤
Q(θ|θ(t))的二次型表示可以使得 最大化θ相对简单. τ, (μ1,Σ1) and (μ2,Σ2) 可以单独的进行最大化.
首先考虑 τ, 有条件τ1 + τ2=1:
和MLE的形式是类似的,二项分布 , 因此:
下一步估计 (μ1,Σ1):
和加权的 MLE就正态分布来说类似
![\boldsymbol{\mu}_1^{(t+1)} = \frac{\sum_{i=1}^n T_{1,i}^{(t)} \mathbf{x}_i}{\sum_{i=1}^n T_{1,i}^{(t)}}]() and
and ![\Sigma_1^{(t+1)} = \frac{\sum_{i=1}^n T_{1,i}^{(t)} (\mathbf{x}_i - \boldsymbol{\mu}_1^{(t+1)}) (\mathbf{x}_i - \boldsymbol{\mu}_1^{(t+1)})^\top }{\sum_{i=1}^n T_{1,i}^{(t)}}]()
对称的:
![\boldsymbol{\mu}_2^{(t+1)} = \frac{\sum_{i=1}^n T_{2,i}^{(t)} \mathbf{x}_i}{\sum_{i=1}^n T_{2,i}^{(t)}}]() and
and ![\Sigma_2^{(t+1)} = \frac{\sum_{i=1}^n T_{2,i}^{(t)} (\mathbf{x}_i - \boldsymbol{\mu}_2^{(t+1)}) (\mathbf{x}_i - \boldsymbol{\mu}_2^{(t+1)})^\top }{\sum_{i=1}^n T_{2,i}^{(t)}}]() .
.
这个例子来自Answers.com的Expectation-maximization algorithm,由于还没有深入体验,心里还说不出一些更通俗易懂的东西来,等研究了并且应用了可能就有所理解和消化。另外,liuxqsmile也做了一些理解和翻译。
============
在网上的源码不多,有一个很好的EM_GM.m,是滑铁卢大学的Patrick P. C. Tsui写的,拿来分享一下:
运行的时候可以如下进行初始化:
1 % matlab code 2 X = zeros(600,2); 3 X(1:200,:) = normrnd(0,1,200,2); 4 X(201:400,:) = normrnd(0,2,200,2); 5 X(401:600,:) = normrnd(0,3,200,2); 6 [W,M,V,L] = EM_GM(X,3,[],[],1,[])
下面是程序源码:
1 %matlab code 2 3 function [W,M,V,L] = EM_GM(X,k,ltol,maxiter,pflag,Init) 4 % [W,M,V,L] = EM_GM(X,k,ltol,maxiter,pflag,Init) 5 % 6 % EM algorithm for k multidimensional Gaussian mixture estimation 7 % 8 % Inputs: 9 % X(n,d) - input data, n=number of observations, d=dimension of variable 10 % k - maximum number of Gaussian components allowed 11 % ltol - percentage of the log likelihood difference between 2 iterations ([] for none) 12 % maxiter - maximum number of iteration allowed ([] for none) 13 % pflag - 1 for plotting GM for 1D or 2D cases only, 0 otherwise ([] for none) 14 % Init - structure of initial W, M, V: Init.W, Init.M, Init.V ([] for none) 15 % 16 % Ouputs: 17 % W(1,k) - estimated weights of GM 18 % M(d,k) - estimated mean vectors of GM 19 % V(d,d,k) - estimated covariance matrices of GM 20 % L - log likelihood of estimates 21 % 22 % Written by 23 % Patrick P. C. Tsui, 24 % PAMI research group 25 % Department of Electrical and Computer Engineering 26 % University of Waterloo, 27 % March, 2006 28 % 29 30 %%%% Validate inputs %%%% 31 if nargin <= 1, 32 disp('EM_GM must have at least 2 inputs: X,k!/n') 33 return 34 elseif nargin == 2, 35 ltol = 0.1; maxiter = 1000; pflag = 0; Init = []; 36 err_X = Verify_X(X); 37 err_k = Verify_k(k); 38 if err_X | err_k, return; end 39 elseif nargin == 3, 40 maxiter = 1000; pflag = 0; Init = []; 41 err_X = Verify_X(X); 42 err_k = Verify_k(k); 43 [ltol,err_ltol] = Verify_ltol(ltol); 44 if err_X | err_k | err_ltol, return; end 45 elseif nargin == 4, 46 pflag = 0; Init = []; 47 err_X = Verify_X(X); 48 err_k = Verify_k(k); 49 [ltol,err_ltol] = Verify_ltol(ltol); 50 [maxiter,err_maxiter] = Verify_maxiter(maxiter); 51 if err_X | err_k | err_ltol | err_maxiter, return; end 52 elseif nargin == 5, 53 Init = []; 54 err_X = Verify_X(X); 55 err_k = Verify_k(k); 56 [ltol,err_ltol] = Verify_ltol(ltol); 57 [maxiter,err_maxiter] = Verify_maxiter(maxiter); 58 [pflag,err_pflag] = Verify_pflag(pflag); 59 if err_X | err_k | err_ltol | err_maxiter | err_pflag, return; end 60 elseif nargin == 6, 61 err_X = Verify_X(X); 62 err_k = Verify_k(k); 63 [ltol,err_ltol] = Verify_ltol(ltol); 64 [maxiter,err_maxiter] = Verify_maxiter(maxiter); 65 [pflag,err_pflag] = Verify_pflag(pflag); 66 [Init,err_Init]=Verify_Init(Init); 67 if err_X | err_k | err_ltol | err_maxiter | err_pflag | err_Init, return; end 68 else 69 disp('EM_GM must have 2 to 6 inputs!'); 70 return 71 end 72 73 %%%% Initialize W, M, V,L %%%% 74 t = cputime; 75 if isempty(Init), 76 [W,M,V] = Init_EM(X,k); L = 0; 77 else 78 W = Init.W; 79 M = Init.M; 80 V = Init.V; 81 end 82 Ln = Likelihood(X,k,W,M,V); % Initialize log likelihood 83 Lo = 2*Ln; 84 85 %%%% EM algorithm %%%% 86 niter = 0; 87 while (abs(100*(Ln-Lo)/Lo)>ltol) & (niter<=maxiter), 88 E = Expectation(X,k,W,M,V); % E-step 89 [W,M,V] = Maximization(X,k,E); % M-step 90 Lo = Ln; 91 Ln = Likelihood(X,k,W,M,V); 92 niter = niter + 1; 93 end 94 L = Ln; 95 96 %%%% Plot 1D or 2D %%%% 97 if pflag==1, 98 [n,d] = size(X); 99 if d>2, 100 disp('Can only plot 1 or 2 dimensional applications!/n'); 101 else 102 Plot_GM(X,k,W,M,V); 103 end 104 elapsed_time = sprintf('CPU time used for EM_GM: %5.2fs',cputime-t); 105 disp(elapsed_time); 106 disp(sprintf('Number of iterations: %d',niter-1)); 107 end 108 %%%%%%%%%%%%%%%%%%%%%% 109 %%%% End of EM_GM %%%% 110 %%%%%%%%%%%%%%%%%%%%%% 111 112 function E = Expectation(X,k,W,M,V) 113 [n,d] = size(X); 114 a = (2*pi)^(0.5*d); 115 S = zeros(1,k); 116 iV = zeros(d,d,k); 117 for j=1:k, 118 if V(:,:,j)==zeros(d,d), V(:,:,j)=ones(d,d)*eps; end 119 S(j) = sqrt(det(V(:,:,j))); 120 iV(:,:,j) = inv(V(:,:,j)); 121 end 122 E = zeros(n,k); 123 for i=1:n, 124 for j=1:k, 125 dXM = X(i,:)'-M(:,j); 126 pl = exp(-0.5*dXM'*iV(:,:,j)*dXM)/(a*S(j)); 127 E(i,j) = W(j)*pl; 128 end 129 E(i,:) = E(i,:)/sum(E(i,:)); 130 end 131 %%%%%%%%%%%%%%%%%%%%%%%%%%%% 132 %%%% End of Expectation %%%% 133 %%%%%%%%%%%%%%%%%%%%%%%%%%%% 134 135 function [W,M,V] = Maximization(X,k,E) 136 [n,d] = size(X); 137 W = zeros(1,k); M = zeros(d,k); 138 V = zeros(d,d,k); 139 for i=1:k, % Compute weights 140 for j=1:n, 141 W(i) = W(i) + E(j,i); 142 M(:,i) = M(:,i) + E(j,i)*X(j,:)'; 143 end 144 M(:,i) = M(:,i)/W(i); 145 end 146 for i=1:k, 147 for j=1:n, 148 dXM = X(j,:)'-M(:,i); 149 V(:,:,i) = V(:,:,i) + E(j,i)*dXM*dXM'; 150 end 151 V(:,:,i) = V(:,:,i)/W(i); 152 end 153 W = W/n; 154 %%%%%%%%%%%%%%%%%%%%%%%%%%%%% 155 %%%% End of Maximization %%%% 156 %%%%%%%%%%%%%%%%%%%%%%%%%%%%% 157 158 function L = Likelihood(X,k,W,M,V) 159 % Compute L based on K. V. Mardia, "Multivariate Analysis", Academic Press, 1979, PP. 96-97 160 % to enchance computational speed 161 [n,d] = size(X); 162 U = mean(X)'; 163 S = cov(X); 164 L = 0; 165 for i=1:k, 166 iV = inv(V(:,:,i)); 167 L = L + W(i)*(-0.5*n*log(det(2*pi*V(:,:,i))) ... 168 -0.5*(n-1)*(trace(iV*S)+(U-M(:,i))'*iV*(U-M(:,i)))); 169 end 170 %%%%%%%%%%%%%%%%%%%%%%%%%%% 171 %%%% End of Likelihood %%%% 172 %%%%%%%%%%%%%%%%%%%%%%%%%%% 173 174 function err_X = Verify_X(X) 175 err_X = 1; 176 [n,d] = size(X); 177 if n<d, 178 disp('Input data must be n x d!/n'); 179 return 180 end 181 err_X = 0; 182 %%%%%%%%%%%%%%%%%%%%%%%%% 183 %%%% End of Verify_X %%%% 184 %%%%%%%%%%%%%%%%%%%%%%%%% 185 186 function err_k = Verify_k(k) 187 err_k = 1; 188 if ~isnumeric(k) | ~isreal(k) | k<1, 189 disp('k must be a real integer >= 1!/n'); 190 return 191 end 192 err_k = 0; 193 %%%%%%%%%%%%%%%%%%%%%%%%% 194 %%%% End of Verify_k %%%% 195 %%%%%%%%%%%%%%%%%%%%%%%%% 196 197 function [ltol,err_ltol] = Verify_ltol(ltol) 198 err_ltol = 1; 199 if isempty(ltol), 200 ltol = 0.1; 201 elseif ~isreal(ltol) | ltol<=0, 202 disp('ltol must be a positive real number!'); 203 return 204 end 205 err_ltol = 0; 206 %%%%%%%%%%%%%%%%%%%%%%%%%%%% 207 %%%% End of Verify_ltol %%%% 208 %%%%%%%%%%%%%%%%%%%%%%%%%%%% 209 210 function [maxiter,err_maxiter] = Verify_maxiter(maxiter) 211 err_maxiter = 1; 212 if isempty(maxiter), 213 maxiter = 1000; 214 elseif ~isreal(maxiter) | maxiter<=0, 215 disp('ltol must be a positive real number!'); 216 return 217 end 218 err_maxiter = 0; 219 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 220 %%%% End of Verify_maxiter %%%% 221 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 222 223 function [pflag,err_pflag] = Verify_pflag(pflag) 224 err_pflag = 1; 225 if isempty(pflag), 226 pflag = 0; 227 elseif pflag~=0 & pflag~=1, 228 disp('Plot flag must be either 0 or 1!/n'); 229 return 230 end 231 err_pflag = 0; 232 %%%%%%%%%%%%%%%%%%%%%%%%%%%%% 233 %%%% End of Verify_pflag %%%% 234 %%%%%%%%%%%%%%%%%%%%%%%%%%%%% 235 236 function [Init,err_Init] = Verify_Init(Init) 237 err_Init = 1; 238 if isempty(Init), 239 % Do nothing; 240 elseif isstruct(Init), 241 [Wd,Wk] = size(Init.W); 242 [Md,Mk] = size(Init.M); 243 [Vd1,Vd2,Vk] = size(Init.V); 244 if Wk~=Mk | Wk~=Vk | Mk~=Vk, 245 disp('k in Init.W(1,k), Init.M(d,k) and Init.V(d,d,k) must equal!/n') 246 return 247 end 248 if Md~=Vd1 | Md~=Vd2 | Vd1~=Vd2, 249 disp('d in Init.W(1,k), Init.M(d,k) and Init.V(d,d,k) must equal!/n') 250 return 251 end 252 else 253 disp('Init must be a structure: W(1,k), M(d,k), V(d,d,k) or []!'); 254 return 255 end 256 err_Init = 0; 257 %%%%%%%%%%%%%%%%%%%%%%%%%%%% 258 %%%% End of Verify_Init %%%% 259 %%%%%%%%%%%%%%%%%%%%%%%%%%%% 260 261 function [W,M,V] = Init_EM(X,k) 262 [n,d] = size(X); 263 [Ci,C] = kmeans(X,k,'Start','cluster', ... 264 'Maxiter',100, ... 265 'EmptyAction','drop', ... 266 'Display','off'); % Ci(nx1) - cluster indeices; C(k,d) - cluster centroid (i.e. mean) 267 while sum(isnan(C))>0, 268 [Ci,C] = kmeans(X,k,'Start','cluster', ... 269 'Maxiter',100, ... 270 'EmptyAction','drop', ... 271 'Display','off'); 272 end 273 M = C'; 274 Vp = repmat(struct('count',0,'X',zeros(n,d)),1,k); 275 for i=1:n, % Separate cluster points 276 Vp(Ci(i)).count = Vp(Ci(i)).count + 1; 277 Vp(Ci(i)).X(Vp(Ci(i)).count,:) = X(i,:); 278 end 279 V = zeros(d,d,k); 280 for i=1:k, 281 W(i) = Vp(i).count/n; 282 V(:,:,i) = cov(Vp(i).X(1:Vp(i).count,:)); 283 end 284 %%%%%%%%%%%%%%%%%%%%%%%% 285 %%%% End of Init_EM %%%% 286 %%%%%%%%%%%%%%%%%%%%%%%% 287 288 function Plot_GM(X,k,W,M,V) 289 [n,d] = size(X); 290 if d>2, 291 disp('Can only plot 1 or 2 dimensional applications!/n'); 292 return 293 end 294 S = zeros(d,k); 295 R1 = zeros(d,k); 296 R2 = zeros(d,k); 297 for i=1:k, % Determine plot range as 4 x standard deviations 298 S(:,i) = sqrt(diag(V(:,:,i))); 299 R1(:,i) = M(:,i)-4*S(:,i); 300 R2(:,i) = M(:,i)+4*S(:,i); 301 end 302 Rmin = min(min(R1)); 303 Rmax = max(max(R2)); 304 R = [Rmin:0.001*(Rmax-Rmin):Rmax]; 305 clf, hold on 306 if d==1, 307 Q = zeros(size(R)); 308 for i=1:k, 309 P = W(i)*normpdf(R,M(:,i),sqrt(V(:,:,i))); 310 Q = Q + P; 311 plot(R,P,'r-'); grid on, 312 end 313 plot(R,Q,'k-'); 314 xlabel('X'); 315 ylabel('Probability density'); 316 else % d==2 317 plot(X(:,1),X(:,2),'r.'); 318 for i=1:k, 319 Plot_Std_Ellipse(M(:,i),V(:,:,i)); 320 end 321 xlabel('1^{st} dimension'); 322 ylabel('2^{nd} dimension'); 323 axis([Rmin Rmax Rmin Rmax]) 324 end 325 title('Gaussian Mixture estimated by EM'); 326 %%%%%%%%%%%%%%%%%%%%%%%% 327 %%%% End of Plot_GM %%%% 328 %%%%%%%%%%%%%%%%%%%%%%%% 329 330 function Plot_Std_Ellipse(M,V) 331 [Ev,D] = eig(V); 332 d = length(M); 333 if V(:,:)==zeros(d,d), 334 V(:,:) = ones(d,d)*eps; 335 end 336 iV = inv(V); 337 % Find the larger projection 338 P = [1,0;0,0]; % X-axis projection operator 339 P1 = P * 2*sqrt(D(1,1)) * Ev(:,1); 340 P2 = P * 2*sqrt(D(2,2)) * Ev(:,2); 341 if abs(P1(1)) >= abs(P2(1)), 342 Plen = P1(1); 343 else 344 Plen = P2(1); 345 end 346 count = 1; 347 step = 0.001*Plen; 348 Contour1 = zeros(2001,2); 349 Contour2 = zeros(2001,2); 350 for x = -Plen:step:Plen, 351 a = iV(2,2); 352 b = x * (iV(1,2)+iV(2,1)); 353 c = (x^2) * iV(1,1) - 1; 354 Root1 = (-b + sqrt(b^2 - 4*a*c))/(2*a); 355 Root2 = (-b - sqrt(b^2 - 4*a*c))/(2*a); 356 if isreal(Root1), 357 Contour1(count,:) = [x,Root1] + M'; 358 Contour2(count,:) = [x,Root2] + M'; 359 count = count + 1; 360 end 361 end 362 Contour1 = Contour1(1:count-1,:); 363 Contour2 = [Contour1(1,:);Contour2(1:count-1,:);Contour1(count-1,:)]; 364 plot(M(1),M(2),'k+'); 365 plot(Contour1(:,1),Contour1(:,2),'k-'); 366 plot(Contour2(:,1),Contour2(:,2),'k-'); 367 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 368 %%%% End of Plot_Std_Ellipse %%%% 369 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
from: http://www.zhizhihu.com/html/y2010/2109.html
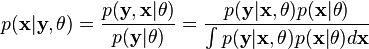








![L(\theta;\mathbf{x},\mathbf{z}) = \exp \left\{ \sum_{i=1}^n \sum_{j=1}^2 \mathbb{I}(z_i=j) \big[ \log \tau_j -\tfrac{1}{2} \log |\Sigma_j| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{d}{2} \log(2\pi) \big] \right\}](http://wpcontent.answcdn.com/math/d/5/3/d53e50b61c8d3465b6bd20e085933f6a.png)
 .
.![\begin{align}Q(\theta|\theta^{(t)}) &= \operatorname{E} [\log L(\theta;\mathbf{x},\mathbf{Z}) ] \\ &= \sum_{i=1}^n \sum_{j=1}^2 T_{j,i}^{(t)} \big[ \log \tau_j -\tfrac{1}{2} \log |\Sigma_j| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{d}{2} \log(2\pi) \big] \end{align}](http://wpcontent.answcdn.com/math/8/4/e/84efae4d173871c8ffb2f53a0c67595f.png)
![\begin{align}\boldsymbol{\tau}^{(t+1)} &= \underset{\boldsymbol{\tau}} \operatorname{arg\,max}\ Q(\theta | \theta^{(t)} ) \\ &= \underset{\boldsymbol{\tau}} \operatorname{arg\,max} \ \left\{ \left[ \sum_{i=1}^n T_{1,i}^{(t)} \right] \log \tau_1 + \left[ \sum_{i=1}^n T_{2,i}^{(t)} \right] \log \tau_2 \right\} \end{align}](http://wpcontent.answcdn.com/math/d/c/8/dc83eff0611209a985b5671d8059f072.png)





 .
.
 浙公网安备 33010602011771号
浙公网安备 33010602011771号