滑动窗口法
滑窗法在算法题中大量应用,其思想简洁强大,但是往往在维护左右指针时候容易出错,现总结整理如下:
1. 介绍
滑动窗口法,也叫尺取法(可能也不一定相等,大概就是这样 =。=),可以用来解决一些查找满足一定条件的连续区间的性质(长度等)的问题。由于区间连续,因此当区间发生变化时,可以通过旧有的计算结果对搜索空间进行剪枝,这样便减少了重复计算,降低了时间复杂度。往往类似于“请找到满足xx的最x的区间(子串、子数组)的xx”这类问题都可以使用该方法进行解决。
2. 引入的小例子
2.1 Leetcode 209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组,返回 0。
示例:
输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。
这道题目最简单的解法自然是枚举每个数组起点和终点,这种解法的时间复杂度是O(N^2)
def solver(nums, s):
optim = len(nums) + 1
for start in range(len(nums)):
summation = 0
for end in range(start, len(nums)):
summation += nums[end]
if summation >= s:
optim = min(optim, end - start + 1)
break
return optim
3. 滑动窗口法的大体框架
滑动窗口算法的思路是这样:
1、我们在字符串 S 中使用双指针中的左右指针技巧,初始化 left = right = 0,把索引闭区间 [left, right] 称为一个「窗口」。
2、我们先不断地增加 right 指针扩大窗口 [left, right],直到窗口中的字符串符合要求(包含了 T 中的所有字符)。
3、此时,我们停止增加 right,转而不断增加 left 指针缩小窗口 [left, right],直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同时,每次增加 left,我们都要更新一轮结果。
4、重复第 2 和第 3 步,直到 right 到达字符串 S 的尽头。
这个思路其实也不难,第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解。左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动。
下面画图理解一下,needs 和 window 相当于计数器,分别记录 T 中字符出现次数和窗口中的相应字符的出现次数。
初始状态:
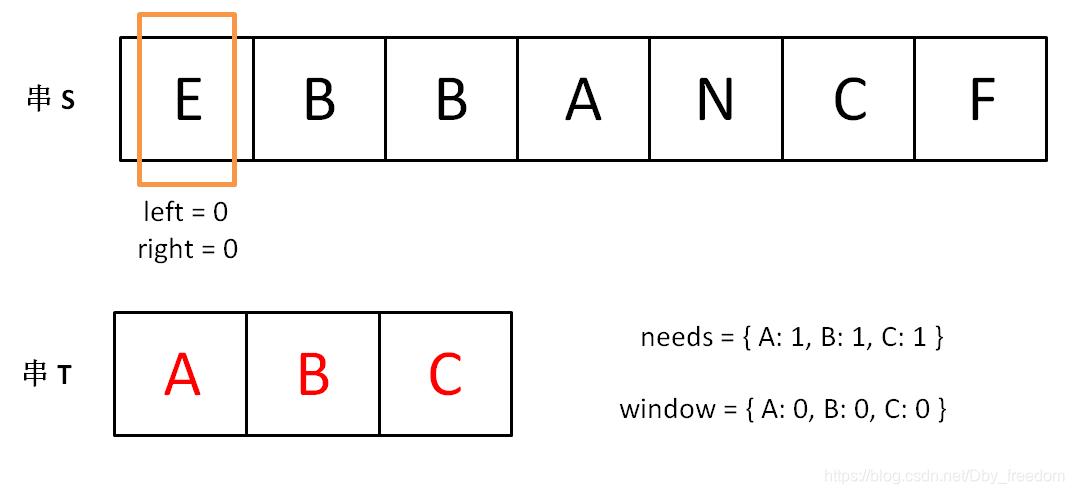
增加 right,直到窗口 [left, right] 包含了 T 中所有字符:
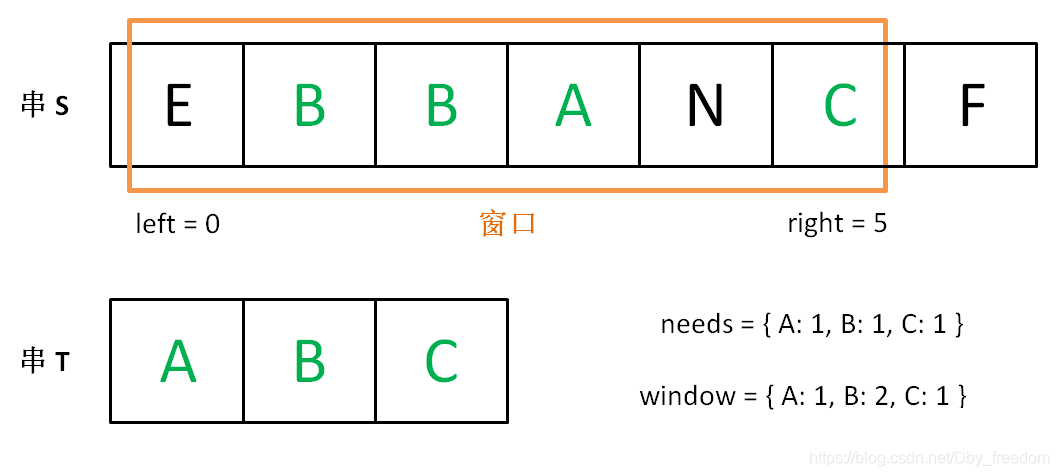
现在开始增加 left,缩小窗口 [left, right]。
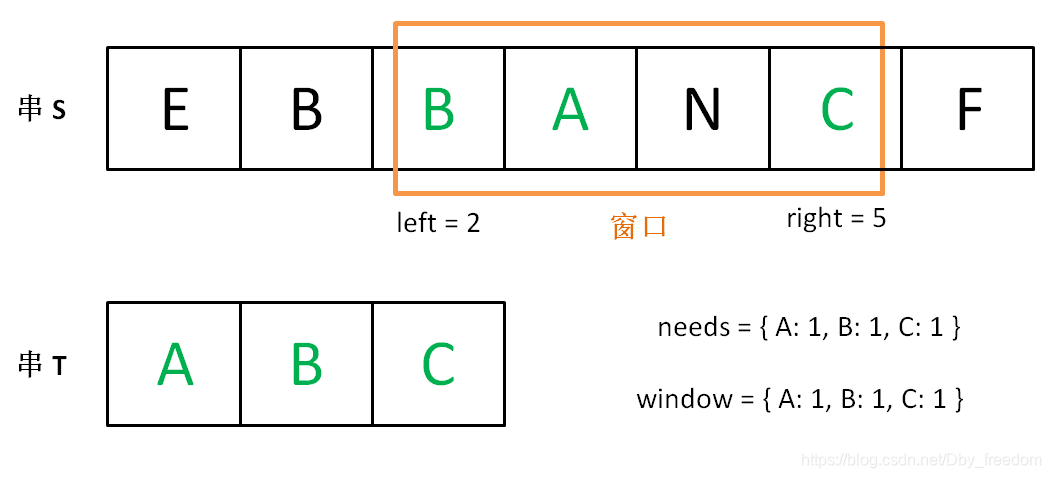
直到窗口中的字符串不再符合要求,left 不再继续移动。
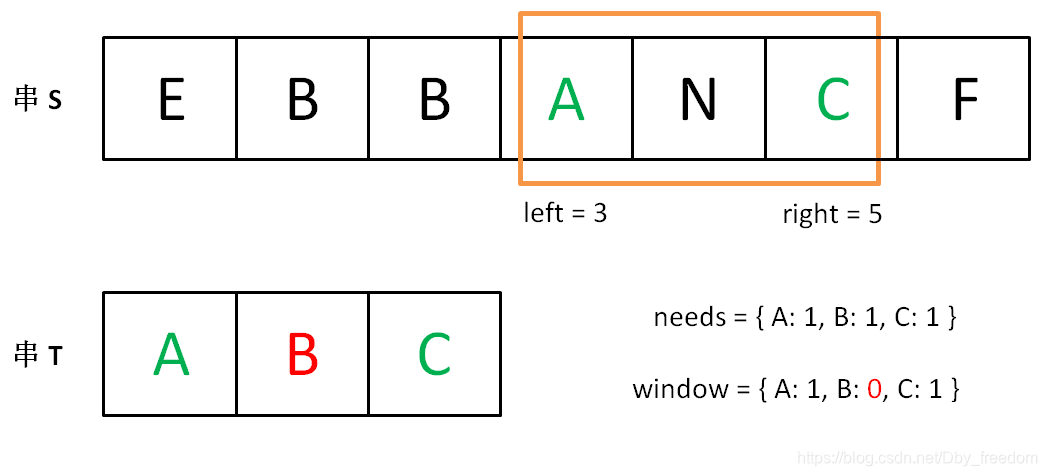
之后重复上述过程,先移动 right,再移动 left…… 直到 right 指针到达字符串 S 的末端,算法结束。
如果你能够理解上述过程,恭喜,你已经完全掌握了滑动窗口算法思想。至于如何具体到问题,如何得出此题的答案,都是编程问题,等会提供一套模板,理解一下就会了。
上述过程可以简单地写出如下伪码框架:
string s, t;
// 在 s 中寻找 t 的「最小覆盖子串」
int left = 0, right = 0;
string res = s;
while(right < s.size()) {
window.add(s[right]);
right++;
// 如果符合要求,移动 left 缩小窗口
while (window 符合要求) {
// 如果这个窗口的子串更短,则更新 res
res = minLen(res, window);
window.remove(s[left]);
left++;
}
}
return res;
如果上述代码你也能够理解,那么你离解题更近了一步。现在就剩下一个比较棘手的问题:如何判断 window 即子串 s[left…right] 是否符合要求,是否包含 t 的所有字符呢?
可以用两个哈希表当作计数器解决。用一个哈希表 needs 记录字符串 t 中包含的字符及出现次数,用另一个哈希表 window 记录当前「窗口」中包含的字符及出现的次数,如果 window 包含所有 needs 中的键,且这些键对应的值都大于等于 needs 中的值,那么就可以知道当前「窗口」符合要求了,可以开始移动 left 指针了。
现在将上面的框架继续细化:
string s, t;
// 在 s 中寻找 t 的「最小覆盖子串」
int left = 0, right = 0;
string res = s;
// 相当于两个计数器
unordered_map<char, int> window;
unordered_map<char, int> needs;
for (char c : t) needs[c]++;
// 记录 window 中已经有多少字符符合要求了
int match = 0;
while (right < s.size()) {
char c1 = s[right];
if (needs.count(c1)) {
window[c1]++; // 加入 window
if (window[c1] == needs[c1])
// 字符 c1 的出现次数符合要求了
match++;
}
right++;
// window 中的字符串已符合 needs 的要求了
while (match == needs.size()) {
// 更新结果 res
res = minLen(res, window);
char c2 = s[left];
if (needs.count(c2)) {
window[c2]--; // 移出 window
if (window[c2] < needs[c2])
// 字符 c2 出现次数不再符合要求
match--;
}
left++;
}
}
return res;
上述代码已经具备完整的逻辑了,只有一处伪码,即更新 res 的地方,不过这个问题太好解决了,直接看解法吧!
string minWindow(string s, string t) {
// 记录最短子串的开始位置和长度
int start = 0, minLen = INT_MAX;
int left = 0, right = 0;
unordered_map<char, int> window;
unordered_map<char, int> needs;
for (char c : t) needs[c]++;
int match = 0;
while (right < s.size()) {
char c1 = s[right];
if (needs.count(c1)) {
window[c1]++;
if (window[c1] == needs[c1])
match++;
}
right++;
while (match == needs.size()) {
if (right - left < minLen) {
// 更新最小子串的位置和长度
start = left;
minLen = right - left;
}
char c2 = s[left];
if (needs.count(c2)) {
window[c2]--;
if (window[c2] < needs[c2])
match--;
}
left++;
}
}
return minLen == INT_MAX ?
"" : s.substr(start, minLen);
}
如果直接甩给你这么一大段代码,我想你的心态是爆炸的,但是通过之前的步步跟进,你是否能够理解这个算法的内在逻辑呢?你是否能清晰看出该算法的结构呢?
这个算法的时间复杂度是 O(M + N),M 和 N 分别是字符串 S 和 T 的长度。因为我们先用 for 循环遍历了字符串 T 来初始化 needs,时间 O(N),之后的两个 while 循环最多执行 2M 次,时间 O(M)。
读者也许认为嵌套的 while 循环复杂度应该是平方级,但是你这样想,while 执行的次数就是双指针 left 和 right 走的总路程,最多是 2M 嘛。
4. 滑动窗口法实例
4.1. LeetCode 76. 最小覆盖子串
给你一个字符串 S、一个字符串 T,请在字符串 S 里面找出:包含 T 所有字母的最小子串。
示例:
输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"
说明:
- 如果 S 中不存这样的子串,则返回空字符串 “”。
- 如果 S 中存在这样的子串,我们保证它是唯一的答案。
思路1:
class Solution {
public:
string minWindow(string s, string t) {
unordered_map<char, int> window;
unordered_map<char, int> target;
for (char c : t) target[c]++;
int left = 0, right = 0;
int windowCnt = 0;
int length = s.size();
int start = 0, minLen = INT_MAX;
while (right < length) {
if (target.count(s[right])) {
window[s[right]]++;
if (window[s[right]] == target[s[right]]) {
windowCnt++;
}
}
right ++;
while (windowCnt == target.size()) {
if (right - left < minLen) {
start = left;
minLen = right - left;
}
char temp = s[left];
if (target.count(temp)) {
window[temp]--;
if (window[temp] < target[temp]) {
windowCnt--;
}
}
left ++;
}
}
return minLen == INT_MAX? "": s.substr(start, minLen);
}
};
4.2 Leetcode 209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组,返回 0。
示例:输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。这道题是上面讲解过的题目,这里套用之前提出的框架再讲一遍。我们设置一个状态为summation,表示当前区间的和,而状态满足的条件是summation >= s,寻找最优值则是去比较当前的最优值以及目前滑动窗口的长度。代入框架即得到了求解该问题的程序:
def minSubArrayLen(s: int, nums: List[int]) -> int:
summation = 0
L, R = 0, -1
optim = len(nums) + 1
while R < len(nums):
while R < len(nums):
R += 1
if R < len(nums):
summation += nums[R]
if summation >= s:
optim = min(optim, R - L + 1)
break
if R == len(nums):
break
while L < R:
summation -= nums[L]
L += 1
if summation >= s:
optim = min(optim, R - L + 1)
else:
break
return optim if optim != len(nums) + 1 else 0
方法2:
class Solution:
def minSubArrayLen(self, s: int, nums: List[int]) -> int:
if not nums:
return 0
left = right = 0
temp_res = 0
res = len(nums) + 1
while right < len(nums):
temp_res += nums[right]
while temp_res >= s:
res = min(res, right - left + 1)
temp_res -= nums[left]
left += 1
right += 1
return res if res != len(nums) + 1 else 0
内部只用一个 while 循环,用于维护滑窗满足要求,不容易出错,是推荐解题思路,模板做法容易出错!
4.3 Leetcode 3. 无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
这道题是寻找无重复字符的最长子串,我们设置一个set来保存当前区间内的字符。对于右端点而言,S[R]不在set当中即满足条件。对于左端点而言,只要让左端点移动到目前S[R]的值第一次出现的位置后面即可,也就是说,不让滑动窗口包含重复的字符(因为重复的字符一定是当前右端点指向的字符)。这道题和前面一道题不同的地方在于,前一道题右端点是从不满足给定条件到移动满足给定条件,而这道题则相反。因此右端点会移动到第一次不满足条件的位置,而左端点则移动到再一次满足条件的位置。代码如下:
def lengthOfLongestSubstring(s: str) -> int:
L, R = 0, -1
optim = 0
status = set()
while R < len(s):
while R < len(s):
R += 1
if R == len(s):
break
if s[R] not in status:
status.add(s[R])
optim = max(optim, R - L + 1)
else:
break
if R == len(s):
break
while L < R:
if s[L] != s[R]:
status.remove(s[L])
L += 1
else:
L += 1
break
return optim
方法2:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
if len(s) < 2:
return len(s)
left = right = 0
base = dict()
length = len(s)
res = 1
while right < length:
if s[right] not in base.keys():
base[s[right]] = right
else:
left = max(left, base[s[right]] + 1)
base[s[right]] = right
res = max(res, right - left + 1)
right += 1
return res
这里用 dict 维护滑窗索引,更直接方便,但是有个问题就是 left 的维护需要仔细思考,不是 left = base[s[right]] + 1 而是 left = max(left, base[s[right]] + 1),即需要保持 left 是不断右移(如对输入 abba,测试会发现,如果使用 left = base[s[right]] + 1,当 right == 3 时,left = base[s[right]] + 1 = 0 +1 = 1,得到错误结果 3,因为当 right == 2 时,left = 2,不加 max 会出现回退)。
方法3:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
if len(s) < 2:
return len(s)
left, right = -1, 0
base = dict()
length = len(s)
res = 1
while right < length:
if s[right] in base.keys() and base[s[right]] > left:
left = base[s[right]]
base[s[right]] = right
res = max(res, right - left)
right += 1
return res
推荐做法,内部只维护一个判定,方法 3 采用不断更新索引,维护 left, right 两个指针。
4.4 Leetcode 1004. 最大连续1的个数 III
给定一个由若干 0 和 1 组成的数组 A,我们最多可以将 K 个值从 0 变成 1 。
返回仅包含 1 的最长(连续)子数组的长度。
示例 1:
输入:A = [1,1,1,0,0,0,1,1,1,1,0], K = 2
输出:6
解释:
[1,1,1,0,0,1,1,1,1,1,1]
粗体数字从 0 翻转到 1,最长的子数组长度为 6。
示例 2:
输入:A = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
输出:10
解释:
[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
粗体数字从 0 翻转到 1,最长的子数组长度为 10。
这道题和上一题一样,右端点移动到第一次不满足条件的位置,而左端点则移动到再一次满足条件的位置。需要满足的条件是,K值大于等于0。当碰到零时,K减去1。代码如下所示:
def longestOnes(A: List[int], K: int) -> int:
L, R = 0, -1
optim = 0
while R < len(A):
while R < len(A):
R += 1
if R == len(A):
break
if A[R] == 0:
K -= 1
if K < 0: #第一次不满足条件
break
else: #满足条件时更新最优值
optim = max(optim, R - L + 1)
if R == len(A):
break
while L < R:
if A[L] == 0:
K += 1
L += 1
if K >= 0:
break
return optim
换双指针解法更容易理解一些
虫取法/双指针:
这个题最开始的想法是 DP,但是没做出来。其实最简单的方法是虫取法或者叫做双指针。
[left, right] 双闭区间表示一个经过一定次数的翻转后已经全部是1的区间。我们要求的长度就是这个区间的最大长度。我们需要把这个区间内的所有0都翻转成1,使用变量 zero 统计该区间内的被翻转的 0 的个数。易知,zero <= K.
我们把 left 和 right 的起始位置都设定为 0,我们每次都向右移动一次right指针代表新判断一个元素。此时,如果right指向的数字是 0,我们需要将 zero+1,代表我们把这个0进行了翻转。然后我们就会想,如果翻转之后 zero > K 了怎么办?所以我们此时需要移动left指针啊!left有可能指向了1,所以需要一直移动直至 zero <= K 为止。
使用 res 保存最大区间长度即可。
这个方法是常见的虫取法,这个虫取法的精髓是保证每次取到的区间是一个严格满足题目要求的区间。具体到这个题目来说就是维护了一个最多翻转 K 个 0 的全 1 区间。只要这个维护是有效的,那么我们就可以根据区间长度更新 res。维护的过程我在上面已经讲解,核心是区间内统计 0 的个数,不过这个统计不是每次都遍历一次区间,而是使用一个变量,这个变量和区间同时维护即可。
class Solution(object):
def longestOnes(self, A, K):
"""
:type A: List[int]
:type K: int
:rtype: int
"""
left,right = 0,0
res = 0
zeros = 0
for right in range(len(A)):
if A[right] == 0:
zeros += 1
while zeros > K:
if A[left] == 0:
zeros -= 1
left += 1
res = max(res, right - left + 1)
return res
对应 C++ 版本:
class Solution {
public:
int longestOnes(vector<int>& A, int K) {
int res = 0;
int left = 0;
int zero = 0;
const int N = A.size();
for (int right = 0; right < N; ++right) {
if (A[right] == 0)
++zero;
while (zero > K) {
if (A[left++] == 0)
--zero;
}
res = max(res, right - left + 1);
}
return res;
}
};
上述代码开起来简洁,但是事实上 res = max(res, right - left + 1); 计算时候 left, right 事实上都是滑窗后移一个位置的索引。
也可从宏观上看,即始终保证滑窗满足条件,更新结果;
4.5. LeetCode 424. Longest Repeating Character Replacement
Given a string s that consists of only uppercase English letters, you can perform at most k operations on that string.
In one operation, you can choose any character of the string and change it to any other uppercase English character.
Find the length of the longest sub-string containing all repeating letters you can get after performing the above operations.
Note:
Both the string’s length and k will not exceed 104.
Example 1:
Input:
s = "ABAB", k = 2
Output:
4
Explanation:
Replace the two 'A's with two 'B's or vice versa.
Example 2:
Input:
s = "AABABBA", k = 1
Output:
4
Explanation:
Replace the one 'A' in the middle with 'B' and form "AABBBBA".
The substring "BBBB" has the longest repeating letters, which is 4.
思路1:
这道题给我们了一个字符串,说我们有k次随意置换任意字符的机会,让我们找出最长的重复字符的字符串。这道题跟之前那道 Longest Substring with At Most K Distinct Characters 很像,都需要用滑动窗口 Sliding Window 来解。
我们首先来想,如果没有k的限制,让我们求把字符串变成只有一个字符重复的字符串需要的最小置换次数,那么就是字符串的总长度减去出现次数最多的字符的个数。
如果加上k的限制,我们其实就是求满足 (子字符串的长度减去出现次数最多的字符个数)<=k 的最大子字符串长度即可,搞清了这一点,我们也就应该知道怎么用滑动窗口来解了吧。
我们用一个变量 start 记录滑动窗口左边界,初始化为0,然后遍历字符串,每次累加出现字符的个数,然后更新出现最多字符的个数,然后我们判断当前滑动窗口是否满足之前说的那个条件,如果不满足,我们就把滑动窗口左边界向右移动一个,并注意去掉的字符要在 counts 里减一,直到满足条件,我们更新结果 res 即可。
需要注意的是,当滑动窗口的左边界向右移动了后,窗口内的相同字母的最大个数貌似可能会改变啊,为啥这里不用更新 maxCnt 呢?这是个好问题,原因是此题让求的是最长的重复子串,maxCnt 相当于卡了一个窗口大小,我们并不希望窗口变小,虽然窗口在滑动,但是之前是出现过跟窗口大小相同的符合题意的子串,缩小窗口没有意义,并不会使结果 res 变大,所以我们才不更新 maxCnt 的,参见代码如下:
class Solution {
public:
int characterReplacement(string s, int k) {
if (s.empty()) return 0;
vector<int> nums(26, 0);
int left = 0, right = 0;
int res = 0, maxCnt = 1;
int length = s.size();
while (right < length) {
nums[s[right] - 'A'] ++;
maxCnt = max(maxCnt, nums[s[right] - 'A']);
while (right - left + 1 - maxCnt > k) {
--nums[s[left] - 'A'];
left++;
}
res = max(res, right - left + 1);
right ++;
}
return res;
}
};
总结
滑动窗口法可以用来解决一些查找满足一定条件的连续区间的性质(长度等)问题,个人认为可以看做是一种双指针方法的特例,两个指针都起始于原点,并一前一后向终点前进。还有一种双指针方法,其两个指针一始一终,并相向靠近,这种方法的内在思想和滑动窗口也非常类似,如Leetcode11. 盛最多水的容器就可以使用这种解法求解。
参考文献
[1] Leetcode刷题总结之滑动窗口法(尺取法)
[2] 【LeetCode】1004. Max Consecutive Ones III 解题报告(C++)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号