力扣题解(151-300)
原文链接:https://gaoyubo.cn/blogs/141ec005.html
一、双指针
151. 反转字符串中的单词
给你一个字符串 s ,请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意:输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
示例 1:
输入:s = "the sky is blue"
输出:"blue is sky the"
示例 2:
输入:s = " hello world "
输出:"world hello"
解释:反转后的字符串中不能存在前导空格和尾随空格
class Solution {
public String reverseWords(String s) {
String[] words = s.split(" ");
StringBuilder sb = new StringBuilder();
for(int i = words.length-1; i >= 0 ;i--){
if(words[i].length() == 0) continue;
sb.append(words[i]);
sb.append(" ");
}
return sb.deleteCharAt(sb.length()-1).toString();
}
public void reverseStr(char[] chars, int i,int j){
while(i != j){
char temp = chars[i];
chars[i++] = chars[j];
chars[j--] = temp;
}
}
}
165. 比较版本号
给你两个版本号 version1 和 version2 ,请你比较它们。
版本号由一个或多个修订号组成,各修订号由一个 '.' 连接。每个修订号由 多位数字 组成,可能包含 前导零 。每个版本号至少包含一个字符。修订号从左到右编号,下标从 0 开始,最左边的修订号下标为 0 ,下一个修订号下标为 1 ,以此类推。例如,2.5.33 和 0.1 都是有效的版本号。
比较版本号时,请按从左到右的顺序依次比较它们的修订号。比较修订号时,只需比较 忽略任何前导零后的整数值 。也就是说,修订号 1 和修订号 001 相等 。如果版本号没有指定某个下标处的修订号,则该修订号视为 0 。例如,版本 1.0 小于版本 1.1 ,因为它们下标为 0 的修订号相同,而下标为 1 的修订号分别为 0 和 1 ,0 < 1 。
返回规则如下:
- 如果
*version1* > *version2*返回1, - 如果
*version1* < *version2*返回-1, - 除此之外返回
0。
示例 1:
输入:version1 = "1.01", version2 = "1.001"
输出:0
解释:忽略前导零,"01" 和 "001" 都表示相同的整数 "1"
class Solution {
public int compareVersion(String version1, String version2) {
//使用.分割
String[] v1 = version1.split("\\.");
String[] v2 = version2.split("\\.");
for(int i = 0; i < v1.length || i < v2.length; i++){
int v1Num = 0,v2Num = 0;
if(i < v1.length){
v1Num = Integer.parseInt(v1[i]);
}
if(i < v2.length){
v2Num = Integer.parseInt(v2[i]);
}
if(v1Num > v2Num) return 1;
if(v1Num < v2Num) return -1;
}
return 0;
}
}
167. 两数之和 II - 输入有序数组
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
class Solution {
public int[] twoSum(int[] numbers, int target) {
int left = 0,right = numbers.length-1;
while(left < right){
int sum = numbers[left] + numbers[right];
if(sum == target) return new int[]{left+1,right+1};
if(sum < target) left++;
else right--;
}
return null;
}
}
189. 轮转数组
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
class Solution {
public void rotate(int[] nums, int k) {
int n = nums.length;
k %= n;
reverse(nums,0,n-1);
reverse(nums,0,k-1);
reverse(nums,k,n-1);
}
public void reverse(int[] nums, int start, int end){
while(start < end){
int temp = nums[end];
nums[end--] = nums[start];
nums[start++] = temp;
}
}
}
202. 快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
class Solution {
public static boolean isHappy(int n) {
/*
n 下个数最大值
` 9 : 81
99 2 * 81
999 3 * 81
.... x * 81
因此对于任何一个数,都不会无限增大下去,有上线,因此如果最后结果不为1,就是进入某个循环中
判断是否进入循环可以采用两种方式
1.hash存储进入过的数,每次比较
2.快慢指针,快指针走两步,满指针走一步
*/
int slow = n;
int fast = getNext(n);
while (fast != 1 && slow != fast){
slow = getNext(slow);
fast = getNext(getNext(fast));
}
return fast == 1;
}
public static int getNext(int number){
int result = 0;
while (number > 0){
int x = number % 10;
number /= 10;
result += Math.pow(x,2);
}
return result;
}
}
203. 移除链表元素
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
示例 1:
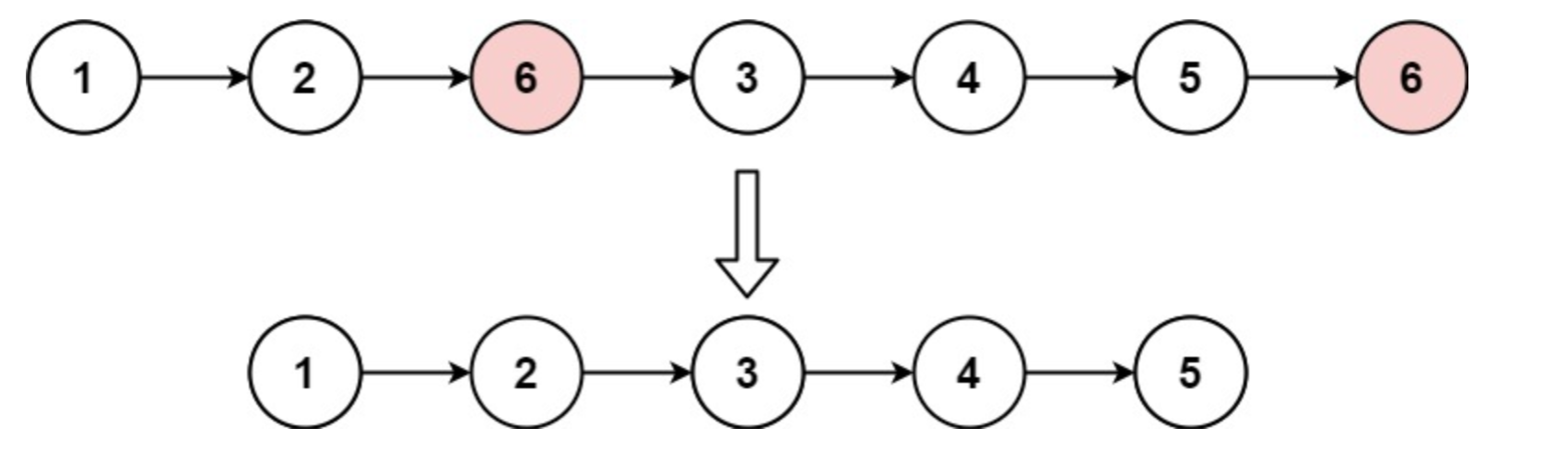
输入:head = [1,2,6,3,4,5,6], val = 6
输出:[1,2,3,4,5]
示例 2:
输入:head = [], val = 1
输出:[]
示例 3:
输入:head = [7,7,7,7], val = 7
输出:[]
提示:
- 列表中的节点数目在范围
[0, 104]内 1 <= Node.val <= 500 <= val <= 50
双指针 pre.next = cur.next;
防止对头结点额外考虑,可以加入虚拟头结点。
public static ListNode removeElements(ListNode head, int val) {
if (head == null) return head;
ListNode preNode = head;
ListNode curNode = head;
while (curNode != null){
if (curNode.val == val){
//如果是头结点
if (curNode == head){
head = head.next;
preNode = head;
}
preNode.next = curNode.next;
}else {
preNode = curNode;
}
curNode = curNode.next;
}
return head;
}
public static ListNode removeElements(ListNode head, int val) {
if(head == null) return null;
//添加虚拟头结点
ListNode newHead = new ListNode(head.val);
newHead.next = head;
ListNode preNode = newHead;
ListNode curNode = newHead;
while (curNode != null){
if (curNode.val == val){
preNode.next = curNode.next;
}else {
preNode = curNode;
}
curNode = curNode.next;
}
return newHead.next;
}
228. 汇总区间
给定一个 无重复元素 的 有序 整数数组 nums 。
返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖,并且不存在属于某个范围但不属于 nums 的数字 x 。
列表中的每个区间范围 [a,b] 应该按如下格式输出:
"a->b",如果a != b"a",如果a == b
示例 1:
输入:nums = [0,1,2,4,5,7]
输出:["0->2","4->5","7"]
解释:区间范围是:
[0,2] --> "0->2"
[4,5] --> "4->5"
[7,7] --> "7"
示例 2:
输入:nums = [0,2,3,4,6,8,9]
输出:["0","2->4","6","8->9"]
解释:区间范围是:
[0,0] --> "0"
[2,4] --> "2->4"
[6,6] --> "6"
[8,9] --> "8->9"
public List<String> summaryRanges(int[] nums) {
int first = 0;
int second = 0;
List<String> list = new ArrayList<>();
while (second <= nums.length-1){
while (second <= nums.length-1 && nums[second] - nums[first] == second - first){
second++;
}
if (nums[first] != nums[second - 1]){
list.add(nums[first] + "->" + nums[second - 1]);
}else {
list.add(String.valueOf(nums[first]));
}
first = second;
}
return list;
}
234. 回文链表(快慢指针+反转、赋值数组双指针)
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
示例 1:

输入:head = [1,2,2,1]
输出:true
示例 2:
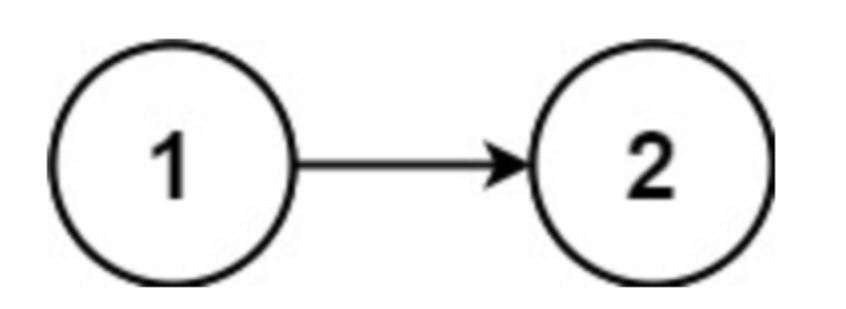
输入:head = [1,2]
输出:false
提示:
- 链表中节点数目在范围
[1, 105]内 0 <= Node.val <= 9
两种方法:
public class Solution234 {
public static boolean isPalindrome(ListNode head) {
ListNode start = head;
ArrayList<Integer> arrayList = new ArrayList<>();
while (start != null){
arrayList.add(start.val);
start = start.next;
}
int front = 0;
int back = arrayList.size()-1;
while (front < back){
if (! (arrayList.get(front++).equals(arrayList.get(back--)))){
return false;
}
}
return true;
}
public static boolean isPalindrome2(ListNode head){
//找到中间节点的位置
ListNode midNode = getMidNode(head);
//反转链表
ListNode secondHead = reverseList(midNode);
//比较
boolean flag = palindromeJudge(midNode,secondHead);
//还原
reverseList(midNode);
return flag;
}
private static boolean palindromeJudge(ListNode midNode, ListNode secondHead) {
ListNode node1 = midNode;
ListNode node2 = secondHead;
while (node2 != null){
if (node1.val != node2.val){
return false;
}
node1 = node1.next;
node2 = node2.next;
}
return true;
}
private static ListNode reverseList(ListNode midNode) {
ListNode preNode = null;
ListNode cur = midNode;
while (cur != null){
ListNode nextNode = cur.next;
cur.next = preNode;
preNode = cur;
cur = nextNode;
}
return preNode;
}
private static ListNode getMidNode(ListNode head) {
//快慢指针
ListNode slow = head;
ListNode fast = head;
while (slow.next != null && fast.next.next != null){
slow = slow.next;
fast = fast.next;
}
return slow;
}
}
283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
public static void moveZeroes(int[] nums) {
int numIndex = 0;
//所有非负数都直接赋值到数组前面
for (int i = 0; i < nums.length; i++) {
if (nums[i] != 0){
nums[numIndex++] = nums[i];
}
}
for (int i = numIndex; i < nums.length; i++) {
nums[i] = 0;
}
}
二、二分法
153. 寻找旋转排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
class Solution {
public static int findMin(int[] nums) {
//最小值如果在nums[mid]的左侧或就是nums[mid],说明nums[mid]-nums[right]一定是升序列
//最小值如果在nums[mid]的右侧,说明nums[mid]-nums[right]一定不是升序列
//反之 也成立
int n = nums.length, left = 0, right = n-1;
while(left < right){
int mid = (left + right) >> 1;
if(nums[mid] < nums[right]){
right = mid;
}else{
left = mid + 1;
}
}
return nums[left];
}
}
154. 寻找旋转排序数组中的最小值 II
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,4] - 若旋转
7次,则可以得到[0,1,4,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个可能存在 重复 元素值的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须尽可能减少整个过程的操作步骤。
示例 1:
输入:nums = [1,3,5]
输出:1
示例 2:
输入:nums = [2,2,2,0,1]
输出:0
class Solution {
public static int findMin(int[] nums) {
int n = nums.length, left = 0, right = n-1;
while(left < right){
int mid = (left + right) >> 1;
if(nums[mid] == nums[right]){
right--;
}
else if(nums[mid] < nums[right]){
right = mid;
}else{
left = mid + 1;
}
}
return nums[left];
}
}
162. 寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题
class Solution {
public int findPeakElement(int[] nums) {
int n = nums.length, left = 0, right = n-1;
if(n == 1) return 0;
//你可以假设 nums[-1] = nums[n] = -∞,所以当nums[mid]<nums[mid+1]时,nums[mid]-nums[right]一定有峰值元素,就算一直是升序,那么因为数组外的为-∞,nums[right]也是峰值元素
while(left <= right){
int mid = left + ((right-left) >> 1);
if(mid == 0) return nums[mid]>nums[mid+1]?mid:mid+1;
if(mid == n-1 || (nums[mid+1] < nums[mid] && nums[mid] > nums[mid-1])) return mid;
if(nums[mid+1] > nums[mid]){
left = mid + 1;
}else{
right = mid -1;
}
}
return 0;
}
}
278. 第一个错误的版本
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, ..., n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
示例 1:
输入:n = 5, bad = 4
输出:4
解释:
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以,4 是第一个错误的版本。
示例 2:
输入:n = 1, bad = 1
输出:1
public int firstBadVersion(int n) {
int left = 0;
int right = n;
int mid = left + ((right - left)>>1);
while (left <= right){
mid = left + ((right - left)>>1);
if (isBadVersion(mid)){
right = mid - 1;
}else {
if (isBadVersion(mid+1)){
return mid+1;
}else {
left = mid + 1;
}
}
}
return mid;
}
三、数学
166. 分数到小数
给定两个整数,分别表示分数的分子 numerator 和分母 denominator,以 字符串形式返回小数 。
如果小数部分为循环小数,则将循环的部分括在括号内。
如果存在多个答案,只需返回 任意一个 。
对于所有给定的输入,保证 答案字符串的长度小于 104 。
示例 1:
输入:numerator = 1, denominator = 2
输出:"0.5"
示例 2:
输入:numerator = 2, denominator = 1
输出:"2"
示例 3:
输入:numerator = 4, denominator = 333
输出:"0.(012)"

class Solution {
public String fractionToDecimal(int numerator, int denominator) {
long a = numerator, b = denominator;
if(a % b == 0) return String.valueOf(a/b);
StringBuilder sb = new StringBuilder();
if(a*b < 0) sb.append("-");
a = Math.abs(a);
b = Math.abs(b);
HashMap<Long,Integer> map = new HashMap<>();
sb.append(String.valueOf(a/b)+".");
a %= b;
while(a != 0){
map.put(a,sb.length());
a *= 10;
sb.append(a/b);
a %= b;
if(map.containsKey(a)){
int index = map.get(a);
return String.format("%s(%s)",sb.substring(0,index),sb.substring(index));
}
}
return sb.toString();
}
}
168. Excel表列名称
给你一个整数 columnNumber ,返回它在 Excel 表中相对应的列名称。
例如:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
示例 1:
输入:columnNumber = 1
输出:"A"
示例 2:
输入:columnNumber = 28
输出:"AB"
示例 3:
输入:columnNumber = 701
输出:"ZY"
示例 4:
输入:columnNumber = 2147483647
输出:"FXSHRXW"
提示:
1 <= columnNumber <= 231 - 1
class Solution {
public static String convertToTitle(int columnNumber) {
/*
A - 1
B- 2
AA 26 + 1
ZY =
*/
if (columnNumber < 27){
return String.valueOf((char)('A'+columnNumber-1) );
}
StringBuilder stringBuilder = new StringBuilder();
while ( columnNumber > 0){
columnNumber--;
char addStr = (char) ('A' + columnNumber % 26);
stringBuilder.append(addStr);
columnNumber /= 26;
}
return stringBuilder.reverse().toString();
}
}
171. Excel 表列序号
给你一个字符串 columnTitle ,表示 Excel 表格中的列名称。返回 该列名称对应的列序号 。
例如:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
示例 1:
输入: columnTitle = "A"
输出: 1
示例 2:
输入: columnTitle = "AB"
输出: 28
示例 3:
输入: columnTitle = "ZY"
输出: 701
提示:
1 <= columnTitle.length <= 7columnTitle仅由大写英文组成columnTitle在范围["A", "FXSHRXW"]内
public static int titleToNumber(String columnTitle) {
int result = 0;
int count = 0;
int pow = 0;
for (int i = columnTitle.length()-1 ; i >= 0 ; i--){
char c = (char) (columnTitle.charAt(i) + 1);
count = (c - 'A');
count *= Math.pow(26,pow++);
result += count;
}
return result;
}
//方法二:变种:因为有 26 个字母,所以相当于 26 进制,每 26 个数则向前进一位
//所以每遍历一位则ans = ans * 26 + num
public static int titleToNumber2(String s) {
int ans = 0;
for(int i=0;i<s.length();i++) {
int num = s.charAt(i) - 'A' + 1;
ans = ans * 26 + num;
}
return ans;
}
172. 阶乘后的零
定一个整数 n ,返回 n! 结果中尾随零的数量。
提示 n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1
示例 1:
输入:n = 3
输出:0
解释:3! = 6 ,不含尾随 0
示例 2:
输入:n = 5
输出:1
解释:5! = 120 ,有一个尾随 0
思路:
对于 10 的话,其实也只有 2 * 5 可以构成,所以我们只需要找有多少对 2/5
把每个乘数再稍微分解下,看一个例子。
`11! = 11 * 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 11 * (2 * 5) * 9 * (4 * 2) * 7 * (3 * 2) * (1 * 5) * (2 * 2) * 3 * (1 * 2) * 1
对于含有 2 的因子的话是 1 * 2, 2 * 2, 3 * 2, 4 * 2 ...
对于含有 5 的因子的话是 1 * 5, 2 * 5...
2的因子比5多,所以找5因子有多少个就可以
5因子出现的位置:5,10,15,20,25(5*5两个),30,35,40,45,50(5*5*2 两个),......125(5*5*5 三个)
发现每5个出现一个5,每25个出现2个5,每125出现3个5....(出现1个5的情况包含了出现2个5的情况)
所以只需计算n/5 + n/25 + n/125 +....
class Solution {
public int trailingZeroes(int n) {
int res = 0;
while(n > 0){
res += n / 5;
n /= 5;
}
return res;
}
}
179. 最大数
给定一组非负整数 nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。
注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。

class Solution {
public static String largestNumber(int[] nums) {
int n = nums.length;
String[] numsS = new String[n];
for(int i = 0; i < n; i++){
numsS[i] = String.valueOf(nums[i]);
}
Arrays.sort(numsS,(a,b)->{
String sa = a +b,sb = b+a;
return sb.compareTo(sa);
});
StringBuilder sb = new StringBuilder();
for(String s: numsS) sb.append(s);
int k = 0;
//防止有000
while(k < sb.length()-1 && sb.charAt(k) == '0') k++;
return sb.substring(k);
}
}
190. 颠倒二进制位
颠倒给定的 32 位无符号整数的二进制位。
提示:
- 请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
- 在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在 示例 2 中,输入表示有符号整数
-3,输出表示有符号整数-1073741825。
示例 1:
输入:n = 00000010100101000001111010011100
输出:964176192 (00111001011110000010100101000000)
解释:输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596,
因此返回 964176192,其二进制表示形式为 00111001011110000010100101000000。
示例 2:
输入:n = 11111111111111111111111111111101
输出:3221225471 (10111111111111111111111111111111)
解释:输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293,
因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。
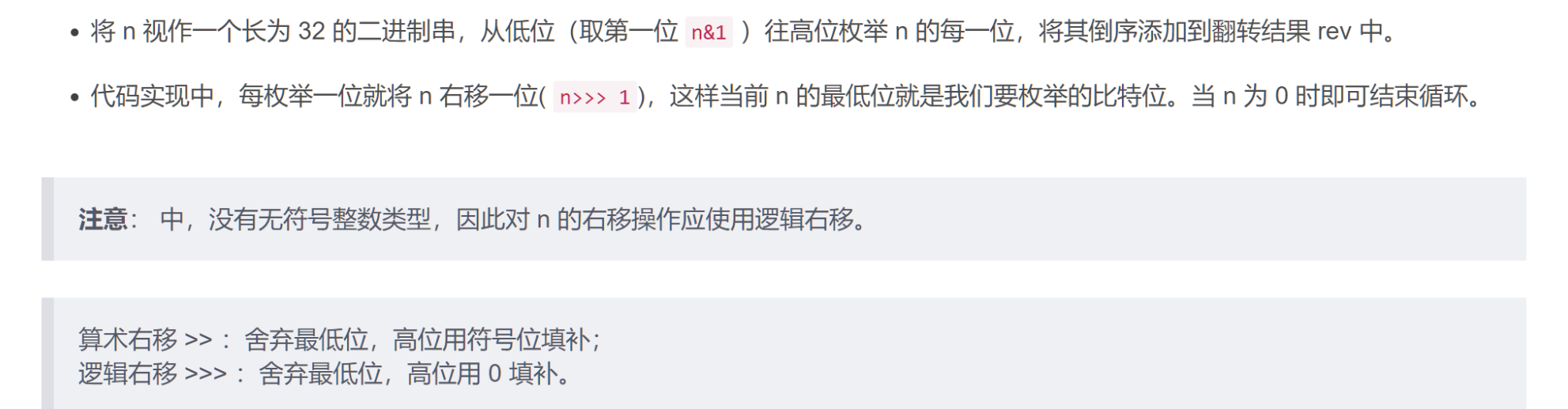
public class Solution {
public static int reverseBits(int n) {
int result = 0;
for (int i = 0; i < 32 && n != 0; i++){
result |= (n & 1) << (31 - i);
n >>>= 1;
}
return result;11
}
}
191. 位1的个数
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为汉明重量)。
提示:
- 请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
- 在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在 示例 3 中,输入表示有符号整数
-3。
示例 1:
输入:n = 00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'
public static int hammingWeight(int n) {
int count = 0;
while(n != 0){
// -1会将最后一个1后面的0 变为1, 再&自己,会将这些1消除
n &= (n-1);
count++;
}
return count;
}
201. 数字范围按位与
给你两个整数 left 和 right ,表示区间 [left, right] ,返回此区间内所有数字 按位与 的结果(包含 left 、right 端点)。
示例 1:
输入:left = 5, right = 7
输出:4
示例 2:
输入:left = 0, right = 0
输出:0
示例 3:
输入:left = 1, right = 2147483647
输出:0
思路:https://blog.csdn.net/qq_34176797/article/details/119054536
class Solution {
public int rangeBitwiseAnd1(int left, int right) {
int zeroCnt = 0;
while(left != right){
left >>= 1;
right >>= 1;
zeroCnt++;
}
return right<<zeroCnt;
}
public int rangeBitwiseAnd(int left, int right) {
while(left < right){
right &= right - 1;//消除最右边的1
}
return right;
}
}
204. 计数质数
给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。
示例 1:
输入:n = 10
输出:4
解释:小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
埃氏筛
- 如果 x 是质数,那么大于 x 的 x 的倍数 2x,3x,… 一定不是质数(所以可以将后面的数标记)
- 从 2x开始标记其实是冗余的,应该直接从 x⋅x开始标记,因为 2x,3x,这些数一定在 x之前就被其他数的倍数标记过了
public int countPrimes(int n) {
int[] noPrime = new int[n];
//noPrime[i]=1: i不是质数
int res = 0;
for(int i = 2; i < n; i++){
if(noPrime[i] == 0){
res++;
for (long j = (long)i * (long)i; j < n; j += i) {
noPrime[(int)j] = 1;
}
}
}
return res;
}
231. 2 的幂
给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false 。
如果存在一个整数 x 使得 n == 2x ,则认为 n 是 2 的幂次方。
public boolean isPowerOfTwo(int n) {
if (n > 0){
//二进制表示是否只有一个1
return (n & (n - 1)) == 0;
}
return false;
}
233. 数字 1 的个数
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。
示例 1:
输入:n = 13
输出:6
示例 2:
输入:n = 0
输出:0
提示:
0 <= n <= 109

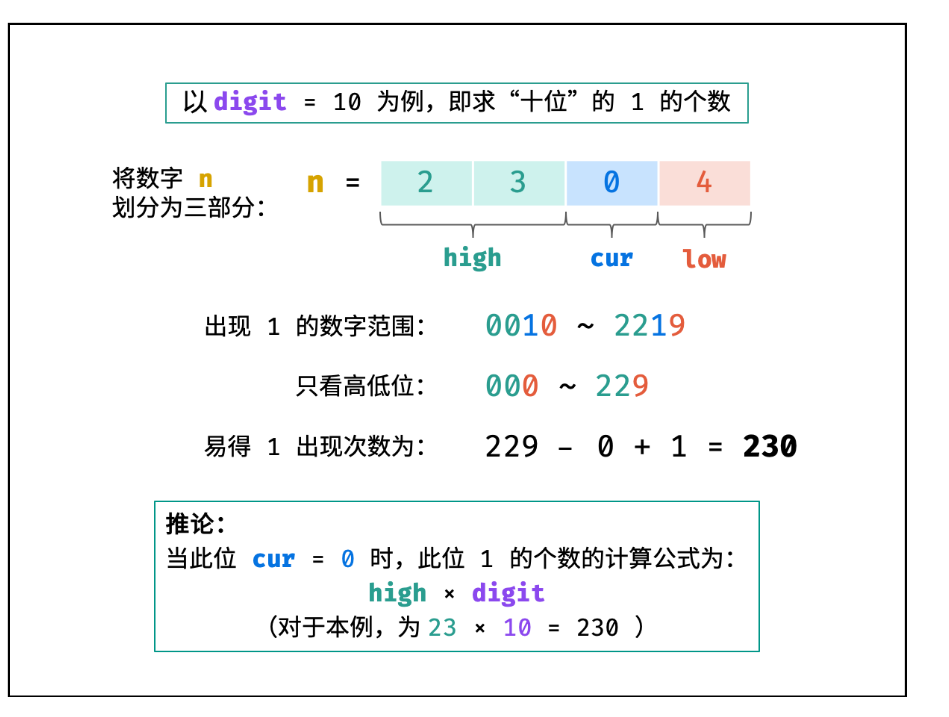


class Solution {
public int countDigitOne(int n) {
int digit = 1,res = 0;
int low = 0,hight = n / 10,cur = n % 10;
while(hight != 0 || cur != 0){
if(cur == 0) res += hight * digit;
else if(cur == 1) res += hight * digit + low + 1;
else res += (hight+1)*digit;
low += digit * cur;
cur = hight % 10;
hight /= 10;
digit *= 10;
}
return res;
}
}
258. 各位相加
示例 1:
输入: num = 38
输出: 2
解释: 各位相加的过程为:
38 --> 3 + 8 --> 11
11 --> 1 + 1 --> 2
由于 2 是一位数,所以返回 2。
示例 2:
输入: num = 0
输出: 0
public static int addDigits(int num) {
if (num < 10 ) return num;
while (num >= 10){
int result = 0;
while (num > 0){
result += num % 10;
num /= 10;
}
num = result;
}
return num;
}
260. 只出现一次的数字 III
给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。

s = 101100
~s = 010011
(~s)+1 = 010100 // 根据补码的定义,这就是 -s 效果:s 的最低 1 左侧取反,右侧不变
s & -s = 000100 // lowbit
public int[] singleNumber(int[] nums) {
int xor = 0;
for(int num:nums){
xor ^= num;
}
int[] ans = new int[2];
//获取最低位的1
int lowBit = xor & (-xor);
for(int num: nums){
if((num & lowBit) == 0) ans[0] ^= num;
else ans[1] ^= num;
}
return ans;
}
263. 丑数
丑数 就是只包含质因数 2、3 和 5 的正整数。
给你一个整数 n ,请你判断 n 是否为 丑数 。如果是,返回 true ;否则,返回 false 。
示例 1:
输入:n = 6
输出:true
解释:6 = 2 × 3
示例 2:
输入:n = 1
输出:true
解释:1 没有质因数,因此它的全部质因数是 {2, 3, 5} 的空集。习惯上将其视作第一个丑数。
示例 3:
输入:n = 14
输出:false
解释:14 不是丑数,因为它包含了另外一个质因数 7 。
class Solution {
/*
对 nnn 反复除以 2,3,5,直到 n 不再包含质因数 2,3,5
若剩下的数等于 1则说明 n不包含其他质因数,是丑数;
否则,说明 n包含其他质因数,不是丑数。
*/
public boolean isUgly(int n) {
if(n <= 0) return false;
int[] factors = {2,3,5};
for(int factor: factors){
while(n % factor == 0){
n /= factor;
}
}
return n == 1;
}
}
268. 丢失的数字
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入:nums = [3,0,1]
输出:2
解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 2:
输入:nums = [0,1]
输出:2
解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1]
输出:8
解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums 中。
示例 4:
输入:nums = [0]
输出:1
解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,因为它没有出现在 nums 中。
public static int missingNumber(int[] nums) {
int sum = -nums.length;
for (int i = 0; i < nums.length; i++){
sum += nums[i];
sum -= i;
}
return Math.abs(sum);
}
四、分治法
五、摩尔投票法求众数
这里我们需要理解摩尔投票中何为占多数元素,也就是元素总占比超过一个比例。\
如果是选出占比最多的一个元素,那么占比需要是大于1/2。`
`如果是选出占比最多的两个元素,那么各个元素占比均需要大于1/3。`
`如果是选出占比最多的m个元素,那么各个元素占比需要是大于1/(m + 1)。
算法思路
第一步,初始化候选人们candidates以及候选人的票数。
第二步,扫描arrays:
扫描过程中候选人的替换以及票数增减规则如下
- 如果与某个候选人匹配,该候选人票数加1,继续扫描arrays,重新开始匹配。
- 如果与所有候选人都不匹配,检查候选人票数,如果为0,替换该候选人,不再往下检查。
- 如果与所有候选人都不匹配,检查候选人票数,如果不为0,继续检查一个候选人。 第三步,扫描结束以后,检查所有候选人的票数是否大于1/(candidates.length + 1)加以验证。如果大于,则候选人成立,不大于则候选人剔除掉。
从算法思路上来看,其实摩尔投票算法的核心思想就是相互抵消。
下面就是摩尔投票算法的典型代表题目。
169. 多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
/*
众数: 占据一半以上的元素
因此可以维持一个变量用于统计元素出现的次数,和假设的众数
假设每个数都有可能是众数,遇到自己就投票,变量+1,
不是自己就变量-1
变量减到0的时候设置众数为自己
原理:每个元素都投自己一票,不属于自己的就-1,由于众数的数量大于一半,因此肯定是众数获胜
*/
class Solution {
public int majorityElement(int[] nums) {
int res = 0,cnt = 0;
for(int num: nums){
if(cnt == 0) res = num;
cnt += res == num?1:-1;
}
return res;
}
}
229. 多数元素 II
给定一个大小为 n 的整数数组,找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。
示例 1:
输入:nums = [3,2,3]
输出:[3]
示例 2:
输入:nums = [1]
输出:[1]
示例 3:
输入:nums = [1,2]
输出:[1,2]
public List<Integer> majorityElement(int[] nums) {
int n = nums.length;
List<Integer> res = new ArrayList<>();
int cand1 = nums[0],count1 = 0;
int cand2 = nums[0],count2 = 0;
for(int num: nums){
if(cand1 == num) count1++;
else if(cand2 == num) count2++;
else if(count1 == 0){
cand1 = num;
count1++;
}else if(count2 == 0){
cand2 = num;
count2++;
}else{
count1--;
count2--;
}
}
count1 = 0;
count2=0;
for(int num: nums){
if(cand1 == num) count1++;
else if(cand2 == num) count2++;
}
if(count1 > n/3) res.add(cand1);
if(count2 > n/3) res.add(cand2);
return res;
}
六、Hash存储
205. 同构字符串
给定两个字符串 s 和 t ,判断它们是否是同构的。
如果 s 中的字符可以按某种映射关系替换得到 t ,那么这两个字符串是同构的。
每个出现的字符都应当映射到另一个字符,同时不改变字符的顺序。不同字符不能映射到同一个字符上,相同字符只能映射到同一个字符上,字符可以映射到自己本身。
示例 1:
输入:s = "egg", t = "add"
输出:true
示例 2:
输入:s = "foo", t = "bar"
输出:false
示例 3:
输入:s = "paper", t = "title"
输出:true
class Solution {
public static boolean isIsomorphic(String s, String t) {
if (s.length() == 1 ) return true;
HashMap<Character,Character> map = new HashMap<>();
HashMap<Character,Character> map2 = new HashMap<>();
for (int i = 0; i < s.length();i++){
if (map.containsKey(s.charAt(i)) && map.get(s.charAt(i)) != t.charAt(i)){
return false;
}else if (!map.containsKey(s.charAt(i))){
map.put(s.charAt(i),t.charAt(i));
}
}
for (int i = 0; i < s.length();i++){
if (map2.containsKey(t.charAt(i)) && map2.get(t.charAt(i)) != s.charAt(i)){
return false;
}else if (!map2.containsKey(t.charAt(i))){
map2.put(t.charAt(i),s.charAt(i));
}
}
return true;
}
}
217. 存在重复元素
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
示例 1:
输入:nums = [1,2,3,1]
输出:true
示例 2:
输入:nums = [1,2,3,4]
输出:false
示例 3:
输入:nums = [1,1,1,3,3,4,3,2,4,2]
输出:true
class Solution {
public static boolean containsDuplicate(int[] nums) {
HashMap<Integer,Integer> map = new HashMap<>();
if (nums.length == 1 ) return false;
for (int num : nums) {
if (!map.containsKey(num)){
map.put(num,1);
}else if (map.get(num) == 1){
return true;
}
}
return false;
}
}
242. 有效的字母异位词
给定两个字符串 *s* 和 *t* ,编写一个函数来判断 *t* 是否是 *s* 的字母异位词。
注意:若 *s* 和 *t* 中每个字符出现的次数都相同,则称 *s* 和 *t* 互为字母异位词。
示例 1:
输入: s = "anagram", t = "nagaram"
输出: true
示例 2:
输入: s = "rat", t = "car"
输出: false
提示:
1 <= s.length, t.length <= 5 * 104s和t仅包含小写字母
两种方法,一种用hash表存储,一种用26个char[]存储
public static boolean isAnagram(String s, String t) {
if (s.length() != t.length()) return false;
HashMap<Character,Integer> map = new HashMap<>();
//存储s的字母出现次数
for (int i = 0; i < s.length(); i++){
if (!map.containsKey(s.charAt(i))){
map.put(s.charAt(i),1);
}else {
map.put(s.charAt(i),map.get(s.charAt(i))+1);
}
}
for (int i = 0; i < t.length(); i++){
if (!map.containsKey(t.charAt(i)) || map.get(t.charAt(i)) == 0){
return false;
}else {
map.put(t.charAt(i),map.get(t.charAt(i))-1);
}
}
return true;
}
public static boolean isAnagram1(String s, String t) {
if (s.length() != t.length()) return false;
char[] letters = new char[26];
for (int i = 0; i < s.length(); i++){
int letterIndex = s.charAt(i) - 'a';
letters[letterIndex]++;
}
for (int i = 0; i < t.length(); i++){
int letterIndex = t.charAt(i) - 'a';
if (letters[letterIndex] == 0){
return false;
}
letters[letterIndex]--;
}
return true;
}
290. 单词规律
给定一种规律 pattern 和一个字符串 s ,判断 s 是否遵循相同的规律。
这里的 遵循 指完全匹配,例如, pattern 里的每个字母和字符串 s 中的每个非空单词之间存在着双向连接的对应规律。
示例1:
输入: pattern = "abba", s = "dog cat cat dog"
输出: true
示例 2:
输入:pattern = "abba", s = "dog cat cat fish"
输出: false
示例 3:
输入: pattern = "aaaa", s = "dog cat cat dog"
输出: false
public static boolean wordPattern(String pattern, String s) {
char[] chars = pattern.toCharArray();
String[] str = s.split(" ");
if (chars.length != str.length) return false;
HashMap<Character, String> map = new HashMap<>();
for (int i = 0; i < chars.length; i++) {
if (!map.containsKey(chars[i])) {
map.put(chars[i], str[i]);
} else {
if (!str[i].equals(map.get(chars[i]))) {
return false;
}
}
}
HashMap<String, Character> map2 = new HashMap<>();
for (int i = 0; i < str.length; i++) {
if (!map2.containsKey(str[i])) {
map2.put(str[i], chars[i]);
} else {
if (chars[i] != map2.get(str[i])) {
return false;
}
}
}
return true;
}
public static boolean wordPattern2(String pattern, String s) {
//存储字符和字符串存在的位置
HashMap<Object, Integer> map = new HashMap<>();
char[] chars = pattern.toCharArray();
String[] str = s.split(" ");
if (chars.length != str.length) return false;
for (int i = 0; i < chars.length; i++){
if (!Objects.equals(map.put(chars[i], i), map.put(str[i], i))){
return false;
}
}
return true;
}
七、队列<--->栈
225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
class MyStack {
public static LinkedList<Integer> list1;
public static LinkedList<Integer> list2;
public MyStack() {
//queue 1保证 存储顺序与stack一致
list1 = new LinkedList<>();
list2 = new LinkedList<>();
}
//使用两个队列实现栈
public void push(int x) {
list2.add(x);
while (!list1.isEmpty()){
list2.add(list1.pop());
}
LinkedList<Integer> temp = list1;
list1 = list2;
list2 = temp;
}
//使用一个队列实现栈
public void pushWithOneList(int x){
int size = list1.size();
list1.add(x);
for(int i = 0; i < size; i++){
list.add(list.pop());
}
}
public int pop() {
return list1.pop();
}
public int top() {
return list1.peek();
}
public boolean empty() {
return list2.isEmpty() && list1.isEmpty();
}
}
232. 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false
class MyQueue {
public static Stack<Integer> stack1;
public static Stack<Integer> stack2;
public MyQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
public void push(int x) {
stack1.push(x);
}
public int pop() {
if (stack2.isEmpty()){
while (!stack1.isEmpty()){
stack2.push(stack1.pop());
}
}
return stack2.pop();
}
public int peek() {
if (stack2.isEmpty()){
while (!stack1.isEmpty()){
stack2.push(stack1.pop());
}
}
return stack2.peek();
}
public boolean empty() {
return stack1.isEmpty() && stack2.isEmpty();
}
}
八、博弈论
292. Nim 游戏
你和你的朋友,两个人一起玩 Nim 游戏:
- 桌子上有一堆石头。
- 你们轮流进行自己的回合, 你作为先手 。
- 每一回合,轮到的人拿掉 1 - 3 块石头。
- 拿掉最后一块石头的人就是获胜者。
假设你们每一步都是最优解。请编写一个函数,来判断你是否可以在给定石头数量为 n 的情况下赢得游戏。如果可以赢,返回 true;否则,返回 false 。
示例 1:
输入:n = 4
输出:false
解释:以下是可能的结果:
1. 移除1颗石头。你的朋友移走了3块石头,包括最后一块。你的朋友赢了。
2. 移除2个石子。你的朋友移走2块石头,包括最后一块。你的朋友赢了。
3.你移走3颗石子。你的朋友移走了最后一块石头。你的朋友赢了。
在所有结果中,你的朋友是赢家。
示例 2:
输入:n = 1
输出:true
示例 3:
输入:n = 2
输出:true
如果为4的倍数,无论选几个,对方都可以使下次还是四的倍数,直到为4,就输了
public boolean canWinNim(int n) {
return (n & 3) != 0;
}
九、动态规划
152. 乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
1 <= nums.length <= 2 * 104-10 <= nums[i] <= 10nums的任何前缀或后缀的乘积都 保证 是一个 32-位 整数
public int maxProduct(int[] nums) {
int len = nums.length;
//计算乘积过程中,当前的结果,要么最大,要么最小都需要保存,也可能为0
//max:i位置结尾最大的数,num > 0时,max * num会增大
//min: i位置结尾最小的数,num < 0时,min * num会更小
//但如果为0,后续的数需要重新计算max和min
int res = Integer.MIN_VALUE, max = 1, min = 1;
for(int i = 0; i < len; i++){
//更换max和min是保证num[i]*max或num[i]*min能得出最大值和最小值
if(nums[i] < 0){
int temp = max;
max = min;
min = temp;
}
max = Math.max(max*nums[i], nums[i]);
min = Math.min(min*nums[i], nums[i]);
res = Math.max(res,max);
}
return res;
}
198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
class Solution {
public int rob(int[] nums) {
int pre2 = 0,cur = 0,max = 0,temp;//pre2前天,cur昨天和今天
for(int num: nums){
temp = cur;//缓存昨天,也就是下一次的前天
cur = Math.max(cur,pre2+num);
pre2 = temp;
max = Math.max(max,cur);
}
return max;
}
}
213. 打家劫舍 II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
class Solution {
public int rob(int[] nums) {
int n = nums.length;
if(n == 1) return nums[0];
if(n == 2) return Math.max(nums[0],nums[1]);
//偷1
int[] dp1 = new int[n];
dp1[0] = nums[0];
dp1[1] = nums[0];
int[] dp2 = new int[n];
//不偷1号
dp2[1] = nums[1];
for(int i = 2; i < n; i++){
dp1[i] = Math.max(dp1[i-1],dp1[i-2]+nums[i]);
dp2[i] = Math.max(dp2[i-1],dp2[i-2]+nums[i]);
}
//因为dp1的首位相连,所以不能选最后的dp[n-1]
return Math.max(dp1[n-2],dp2[n-1]);
}
}
221. 最大正方形
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
class Solution {
public int maximalSquare(char[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int[][] dp = new int[m+1][n+1];
int res = 0;
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(matrix[i-1][j-1] == '1'){
dp[i][j] = Math.min(Math.min(dp[i-1][j-1],dp[i-1][j]),dp[i][j-1]) + 1;
res = Math.max(res,dp[i][j]);
}
}
}
return res*res;
}
}
238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(*n*) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] result = new int[n];
result[0] = 1;
for(int i = 1; i < n; i++){
result[i] = nums[i-1] * result[i-1];
}
int rightRes = 1;
for(int i = n - 1; i >= 0; i--){
result[i] = result[i] * rightRes;
rightRes *= nums[i];
}
return result;
}
264. 丑数 II
给你一个整数 n ,请你找出并返回第 n 个 丑数 。
丑数 就是质因子只包含 2、3 和 5 的正整数。
示例 1:
输入:n = 10
输出:12
解释:[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。
public int nthUglyNumber(int n) {
int[] dp = new int[n+1];
//dp[i]--->第i个丑数
dp[1] = 1;
int p2 = 1,p3 = 1,p5 = 1;
for(int i = 2; i <= n; i++){
int num2 = dp[p2]*2,num3 = dp[p3]*3,num5 = dp[p5]*5;
dp[i] = Math.min(num2,Math.min(num3,num5));
if(dp[i] == num2) p2++;
if(dp[i] == num3) p3++;
if(dp[i] == num5) p5++;
}
return dp[n];
}
274. H 指数
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。
根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 是指他(她)至少发表了 h 篇论文,并且每篇论文 至少 被引用 h 次。如果 h 有多种可能的值,h 指数 是其中最大的那个。
示例 1:
输入:citations = [3,0,6,1,5]
输出:3
解释:给定数组表示研究者总共有 5 篇论文,每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
由于研究者有 3 篇论文每篇 至少 被引用了 3 次,其余两篇论文每篇被引用 不多于 3 次,所以她的 h 指数是 3。
public int hIndex(int[] citations) {
int n = citations.length;
//dp[i]-->引用次数为i的文章,有几篇,H<=n,所以引用次数>n的,当做n计算
int[] dp = new int[n+1];
for(int time: citations){
if(time >= n) dp[n]++;
else dp[time]++;
}
int totalCnt = 0;
for(int i = n; i >= 0; i--){
totalCnt += dp[i];
//总篇数 > i引用数
if(totalCnt >= i) return i;
}
return 0;
}
275. H 指数 II
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数,citations 已经按照 升序排列 。计算并返回该研究者的 h 指数。
h 指数的定义:h 代表“高引用次数”(high citations),一名科研人员的 h 指数是指他(她)的 (n 篇论文中)至少 有 h 篇论文分别被引用了至少 h 次。
请你设计并实现对数时间复杂度的算法解决此问题。
public int hIndex(int[] citations) {
int n = citations.length;
int left = 0, right =n-1;
int mid = 0;
while(left <= right){
mid = left + (right - left) /2;
//满足条件,需要找到不满足条件的最极限的位置,因此更换区间
if(citations[mid] >= n-mid) right = mid -1;
//不满足条件,需要先找到满足条件的位置,更换区间
else left = mid + 1;
}
//不相等时,left右移了,所以n-left
return n - left;
}
279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
public int numSquares(int n) {
//dp[i]->>i的最少完全平方和数
int[] dp = new int[n+1];
for(int i = 1; i <= n; i++){
int minCnt = Integer.MAX_VALUE;
for(int j = 1; j *j <=i; j++){
minCnt = Math.min(minCnt,dp[i - j*j]);
}
dp[i] = minCnt + 1;
}
return dp[n];
}
309. 买卖股票的最佳时机含冷冻期
给定一个整数数组prices,其中第 prices[i] 表示第 *i* 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
//dp[i][0]当前没股,当天没卖
//dp[i][1]当天持股
//dp[i][2]当天卖了
int[][] dp = new int[n][3];
dp[0][1] = -prices[0];
for(int i = 1;i < n; i++){
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][2]);
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
dp[i][2] = dp[i-1][1]+prices[i];
}
return Math.max(dp[n-1][0],dp[n-1][2]);
}
}
区间DP
312. 戳气球

有 n 个气球,编号为0 到 n - 1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。戳破第 i 个气球,你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球。
求所能获得硬币的最大数量。
class Solution {
public int maxCoins(int[] nums) {
int n = nums.length;
int[] arr = new int[n+2];
arr[0] = arr[n+1] = 1;
System.arraycopy(nums,0,arr,1,nums.length);
int[][] dp = new int[n+2][n+2];
for(int len = 3; len <= n+2; len++){
for(int l = 0; l + len - 1 < n + 2;l++){
int r = l + len - 1;
for(int k = l + 1; k < r; k++){
dp[l][r] = Math.max(dp[l][r],dp[l][k]+dp[k][r]+arr[l]*arr[k]*arr[r]);
}
}
}
return dp[0][n+1];
}
}
十、模拟
227. 基本计算器 II
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。
你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。
注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
示例 1:
输入:s = "3+2*2"
输出:7
示例 2:
输入:s = " 3/2 "
输出:1
示例 3:
输入:s = " 3+5 / 2 "
输出:5
class Solution {
//维护一个优先级Map,双括号初始化
Map<Character,Integer> map = new HashMap<>(){{
put('-',1);
put('+',1);
put('*',2);
put('/',2);
put('%',2);
put('^',3);
}};
public int calculate(String s) {
//去除空格
s = s.replaceAll(" ","");
char[] cs = s.toCharArray();
int n = s.length();
//数字栈
Deque<Integer> nums = new ArrayDeque<>();
nums.addLast(0);//防止数字是负数
//操作数栈
Deque<Character> ops = new ArrayDeque<>();
for(int i = 0; i < n; i++){
//判断是否为()
char c = cs[i];
if(c == '('){
ops.addLast(c);
}else if(c == ')'){
//计算之前的
while(!ops.isEmpty() && ops.peekLast() != '('){
cal(nums,ops);
}
ops.pollLast();//拿出(
}else if(isNumber(c)){//是否为数字
int num = 0, j = i;
while(j < n && isNumber(cs[j])){
//数字可能为多位:123
num = num * 10 + (cs[j++] - '0');
}
nums.addLast(num);
i = j-1;
}else{//操作符
//防止紧挨着:(-5+3)或 2++7 ----》(0-5+3)和2+0+7
if(i > 0 && (cs[i-1] == '(' || cs[i-1] == '+' || cs[i-1] == '-')){
nums.addLast(0);
}
//一直计算栈内的,直到左括号,需要有右括号抵消左括号,之前已经判断了
while(!ops.isEmpty() && ops.peekLast() != '('){
char opPeek = ops.peekLast();
if(map.get(opPeek) >= map.get(c)){
cal(nums,ops);
}else break;
}
ops.addLast(c);
}
}
//计算剩下的
while(!ops.isEmpty()) cal(nums,ops);
return nums.peekLast();
}
public boolean isNumber(char c){
return Character.isDigit(c);
}
public void cal(Deque<Integer> nums, Deque<Character> ops){
if(nums.isEmpty() || nums.size()<2 || ops.isEmpty()) return;
// num1 op num2
int num2 = nums.pollLast(),num1 = nums.pollLast();
char op = ops.pollLast();
int ans = 0;
switch (op){
case '+':
ans = num1 + num2;
break;
case '-':
ans = num1 - num2;
break;
case '*':
ans = num1 * num2;
break;
case '/':
ans = num1 / num2;
break;
case '%':
ans = num1 % num2;
break;
case '^':
ans = (int) Math.pow(num1,num2);//计算次幂
break;
}
nums.addLast(ans);
}
}
237. 删除链表中的节点
有一个单链表的 head,我们想删除它其中的一个节点 node。
给你一个需要删除的节点 node 。你将 无法访问 第一个节点 head。
链表的所有值都是 唯一的,并且保证给定的节点 node 不是链表中的最后一个节点。
删除给定的节点。注意,删除节点并不是指从内存中删除它。这里的意思是:
- 给定节点的值不应该存在于链表中。
- 链表中的节点数应该减少 1。
node前面的所有值顺序相同。node后面的所有值顺序相同。
自定义测试:
- 对于输入,你应该提供整个链表
head和要给出的节点node。node不应该是链表的最后一个节点,而应该是链表中的一个实际节点。 - 我们将构建链表,并将节点传递给你的函数。
- 输出将是调用你函数后的整个链表。
示例 1:
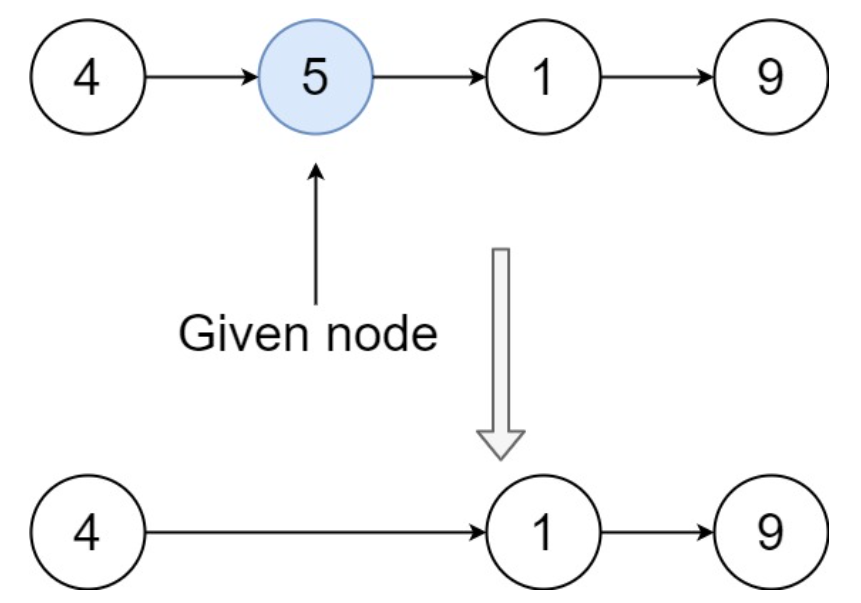
输入:head = [4,5,1,9], node = 5
输出:[4,1,9]
解释:指定链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9
public void deleteNode(ListNode node) {
node.val = node.next.val;
node.next = node.next.next;
}
240. 搜索二维矩阵 II
编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:
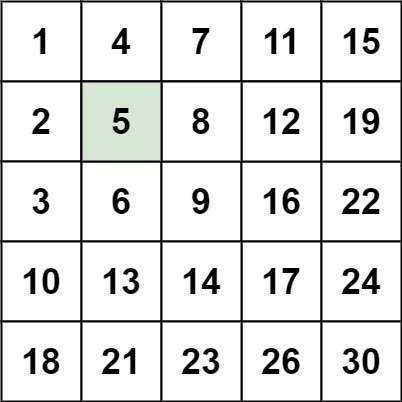
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length,n = matrix[0].length;
int row = m-1,col = 0;
while(row >= 0 && col < n){
if(matrix[row][col] == target) return true;
else if(matrix[row][col] < target) col++;
else row--;
}
return false;
}
299. 猜数字游戏
你在和朋友一起玩 猜数字(Bulls and Cows)游戏,该游戏规则如下:
写出一个秘密数字,并请朋友猜这个数字是多少。朋友每猜测一次,你就会给他一个包含下述信息的提示:
- 猜测数字中有多少位属于数字和确切位置都猜对了(称为 "Bulls",公牛),
- 有多少位属于数字猜对了但是位置不对(称为 "Cows",奶牛)。也就是说,这次猜测中有多少位非公牛数字可以通过重新排列转换成公牛数字。
给你一个秘密数字 secret 和朋友猜测的数字 guess ,请你返回对朋友这次猜测的提示。
提示的格式为 "xAyB" ,x 是公牛个数, y 是奶牛个数,A 表示公牛,B 表示奶牛。
请注意秘密数字和朋友猜测的数字都可能含有重复数字。
示例 1:
输入:secret = "1807", guess = "7810"
输出:"1A3B"
解释:数字和位置都对(公牛)用 '|' 连接,数字猜对位置不对(奶牛)的采用斜体加粗标识。
"1807"
|
"7810"
示例 2:
输入:secret = "1123", guess = "0111"
输出:"1A1B"
解释:数字和位置都对(公牛)用 '|' 连接,数字猜对位置不对(奶牛)的采用斜体加粗标识。
"1123" "1123"
| or |
"0111" "0111"
注意,两个不匹配的 1 中,只有一个会算作奶牛(数字猜对位置不对)。通过重新排列非公牛数字,其中仅有一个 1 可以成为公牛数字。
public String getHint(String secret, String guess) {
int n = secret.length();
int a = 0,b = 0;
int[] cnt1 = new int[10],cnt2 = new int[10];
for(int i = 0; i < n; i++){
int c1 = secret.charAt(i)-'0';
int c2 = guess.charAt(i)-'0';
if(c1 == c2) a++;
else{
cnt1[c1]++;
cnt2[c2]++;
}
}
for(int i = 0; i < 10; i++){
b += Math.min(cnt1[i],cnt2[i]);
}
return a+"A"+b+"B";
}
十一、排序
基数排序
164. 最大间距
给定一个无序的数组 nums,返回 数组在排序之后,相邻元素之间最大的差值 。如果数组元素个数小于 2,则返回 0 。
您必须编写一个在「线性时间」内运行并使用「线性额外空间」的算法。
示例 1:
输入: nums = [3,6,9,1]
输出: 3
解释: 排序后的数组是 [1,3,6,9], 其中相邻元素 (3,6) 和 (6,9) 之间都存在最大差值 3。
示例 2:
输入: nums = [10]
输出: 0
解释: 数组元素个数小于 2,因此返回 0。
class Solution {
public int maximumGap(int[] nums) {
int n = nums.length;
if(n < 2) return 0;
int[] buf = new int[n];
int max = Arrays.stream(nums).max().getAsInt();
int exp = 1;
while(max >= exp){
int[] cnt = new int[10];
//将最后一位进行存储
for(int i = 0; i < n; i++){
int digit = (nums[i]/exp)%10;
cnt[digit]++;
}
//将存储累加,作为num的存储位置
for(int i = 1; i < 10; i++){
cnt[i] += cnt[i-1];
}
//重新存储num位置
for(int i = 0; i < n; i++){
int digit = (nums[i]/exp)%10;
buf[--cnt[digit]] = nums[i];
}
System.arraycopy(buf,0,nums,0,n);
exp *= 10;
}
int res = 0;
for(int i = 1; i < n; i++){
res = Math.max(res,nums[i]-nums[i-1]);
}
return res;
}
}
十二、贪心
十三、滑动窗口
209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
思路:

class Solution {
public int minSubArrayLen(int target, int[] nums) {
int n = nums.length;
if(n == 0) return 0;
int start = 0,end = 0,sum = 0;
int res = Integer.MAX_VALUE;
while(end < n){
sum += nums[end++];
while(sum >= target){
res = Math.min(res,end-start);
sum -= nums[start++];
}
}
return res == Integer.MAX_VALUE?0:res;
}
}
239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
Deque<Integer> queue = new LinkedList<>();
for(int i = 0; i < k; i++){
//保证queue的单调递减
while(!queue.isEmpty() && queue.peekLast() < nums[i]){
queue.removeLast();
}
queue.addLast(nums[i]);
}
int[] res = new int[n - k + 1];
res[0] = queue.peekFirst();
for(int i = k; i < n; i++){
//防止size超过k
if(queue.peekFirst() == nums[i-k]){
queue.removeFirst();
}
//保证queue的单调递减
while(!queue.isEmpty() && queue.peekLast() < nums[i]){
queue.removeLast();
}
queue.addLast(nums[i]);
res[i - k + 1] = queue.peekFirst();
}
return res;
}
public static int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
Deque<Integer> queue = new LinkedList<>();
for(int i = 0; i < k; i++){
//保证queue的单调递减
while(!queue.isEmpty() && queue.peekLast() < nums[i]){
queue.removeLast();
}
queue.addLast(nums[i]);
}
int[] res = new int[n - k + 1];
res[0] = queue.peekFirst();
for(int i = k; i < n; i++){
int max = queue.peekFirst();
//防止size超过k
if(max == nums[i-k]){
queue.removeFirst();
}
//保证queue的单调递减
if(nums[i] > max){
queue.clear();
}else{
while(!queue.isEmpty() && queue.peekLast() < nums[i]){
queue.removeLast();
}
}
queue.addLast(nums[i]);
res[i - k + 1] = queue.peekFirst();
}
return res;
}
TreeSet维护窗口
220. 存在重复元素 III
给你一个整数数组 nums 和两个整数 indexDiff 和 valueDiff 。
找出满足下述条件的下标对 (i, j):
i != j,abs(i - j) <= indexDiffabs(nums[i] - nums[j]) <= valueDiff
如果存在,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [1,2,3,1], indexDiff = 3, valueDiff = 0
输出:true
解释:可以找出 (i, j) = (0, 3) 。
满足下述 3 个条件:
i != j --> 0 != 3
abs(i - j) <= indexDiff --> abs(0 - 3) <= 3
abs(nums[i] - nums[j]) <= valueDiff --> abs(1 - 1) <= 0
对于任意一个位置 i(假设其值为 u),我们其实是希望在下标范围为 [max(0,i−k),i) 内找到值范围在 [u−t,u+t]的数。
-
维护一个TreeSet,方便二分查找出比num[i]大和小的值
-
保证TreeSet的size<indexDiff,也就保证了找出的值都符合下标要求
- floor(E e) 方法返回在这个集合中小于或者等于给定元素的最大元素,如果不存在这样的元素,返回null.
- ceiling(E e) 方法返回在这个集合中大于或者等于给定元素的最小元素,如果不存在这样的元素,返回null.
-
使用这两个方法可以保证差值绝对值最小,如果差值最小的都不能满足,说明num[i]和找到的数不能满足题目要求
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int indexDiff, int valueDiff) {
int n = nums.length;
TreeSet<Integer> treeSet = new TreeSet<>();
for(int i = 0; i < n; i++){
Integer less = treeSet.floor(nums[i]);
Integer bigger = treeSet.ceiling(nums[i]);
if(less != null && nums[i] - less <= valueDiff) return true;
if(bigger != null && bigger - nums[i] <= valueDiff) return true;
treeSet.add(nums[i]);
if(i >= indexDiff){//超过维护大小,移除最前面的
treeSet.remove(nums[i-indexDiff]);
}
}
return false;
}
}
十四、深度优先搜索
200. 岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
class Solution {
public int numIslands(char[][] grid) {
int m = grid.length;
int n = grid[0].length;
int res = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j] == '1'){
res++;
process(grid,i,j);
}
}
}
return res;
}
public void process(char[][] grid,int i , int j){
if(i <0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] != '1'){
return;
}
grid[i][j] = '2';
process(grid,i-1,j);
process(grid,i+1,j);
process(grid,i,j-1);
process(grid,i,j+1);
}
}
216. 组合总和 III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
class Solution {
public List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
dfs(result,path,n,1,k);
return result;
}
public void dfs(List<List<Integer>> result,List<Integer> path,int less,int cur,int maxCnt){
if(path.size() == maxCnt){
if(less == 0) result.add(new ArrayList(path));
return;
}
for(int i = cur; i <= 9; i++){
if(i > less) return;//剪枝
path.add(i);
dfs(result,path,less-i,i+1,maxCnt);
path.remove(path.size()-1);
}
}
}
222. 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
class Solution {
public int countNodes(TreeNode root) {
if(root == null) return 0;
int leftDeep = getDeep(root.left);
int rightDeep = getDeep(root.right);
if( leftDeep== rightDeep){
return (int)Math.pow(2,leftDeep) + countNodes(root.right);
}
return (int)Math.pow(2,rightDeep) + countNodes(root.left);
}
public int getDeep(TreeNode node){
if(node == null) return 0;
return Math.max(getDeep(node.left),getDeep(node.right))+1;
}
}
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
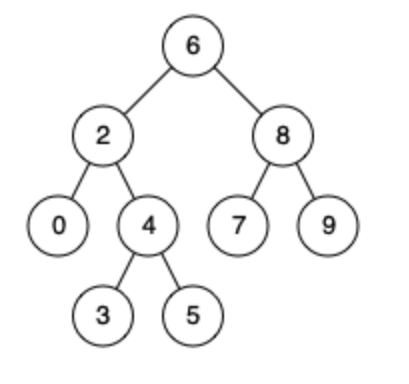
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//都在左边
if(p.val < root.val && q.val < root.val){
return lowestCommonAncestor(root.left,p,q);
}else if(p.val > root.val && q.val > root.val){
//都在右边
return lowestCommonAncestor(root.right,p,q);
}else{
//一左一右或者有一个==root
return root;
}
}
}
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
if(left == null) return right;
if(right == null) return left;
return root;
}
}
241. 为运算表达式设计优先级
给你一个由数字和运算符组成的字符串 expression ,按不同优先级组合数字和运算符,计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。
生成的测试用例满足其对应输出值符合 32 位整数范围,不同结果的数量不超过 104 。
示例 1:
输入:expression = "2-1-1"
输出:[0,2]
解释:
((2-1)-1) = 0
(2-(1-1)) = 2
示例 2:
输入:expression = "2*3-4*5"
输出:[-34,-14,-10,-10,10]
解释:
(2*(3-(4*5))) = -34
((2*3)-(4*5)) = -14
((2*(3-4))*5) = -10
(2*((3-4)*5)) = -10
(((2*3)-4)*5) = 10
class Solution {
char[] cs;
public List<Integer> diffWaysToCompute(String expression) {
cs = expression.toCharArray();
return dfs(0,cs.length-1);
}
public List<Integer> dfs(int l,int r){
List<Integer> res = new ArrayList<>();
for(int i = l; i <= r; i++){
//找到操作符
if(Character.isDigit(cs[i])) continue;
//获取左右两边的结果集
List<Integer> l1 = dfs(l,i-1),l2 = dfs(i+1,r);
for(int a : l1){
for(int b: l2){
//计算左右两边可能的结果
int cur = 0;
if(cs[i] == '+') cur = a + b;
else if(cs[i] == '-') cur = a - b;
else cur = a*b;
res.add(cur);
}
}
}
//没有操作符了,[l,r]都是数字
if(res.isEmpty()){
int num = 0;
for(int i = l; i <= r; i++){
num = num * 10 + (cs[i]- '0');
}
res.add(num);
}
return res;
}
}
十五、单调栈
十九、回溯
282. 给表达式添加运算符
给定一个仅包含数字 0-9 的字符串 num 和一个目标值整数 target ,在 num 的数字之间添加 二元 运算符(不是一元)+、- 或 * ,返回 所有 能够得到 target 的表达式。
注意,返回表达式中的操作数 不应该 包含前导零。
示例 1:
输入: num = "123", target = 6
输出: ["1+2+3", "1*2*3"]
解释: “1*2*3” 和 “1+2+3” 的值都是6。
class Solution {
public List<String> addOperators(String num, int target) {
List<String> result = new ArrayList<>();
dfs(result,"",0,0,0,target,num);
return result;
}
public void dfs(List<String> result,String path,int index,long preAns,long curAns,int target,String num){
if(index == num.length()){
if(curAns == target) result.add(path);
return;
}
for(int i = index; i < num.length(); i++){
//保证没有01,012等切割出来的next
if(i != index && num.charAt(index) == '0') break;
long next = Long.parseLong(num.substring(index,i+1));
if(index == 0){//前面没数
dfs(result,""+next,i+1,next,next,target,num);
}else{
dfs(result,path+"+"+next,i+1,next,curAns+next,target,num);
dfs(result,path+"-"+next,i+1,-next,curAns-next,target,num);
long x = preAns * next;
dfs(result,path+"*"+next,i+1,x,curAns-preAns+x,target,num);
}
}
}
}
301. 删除无效的括号
给你一个由若干括号和字母组成的字符串 s ,删除最小数量的无效括号,使得输入的字符串有效。
返回所有可能的结果。答案可以按 任意顺序 返回。
示例 1:
输入:s = "()())()"
输出:["(())()","()()()"]
示例 2:
输入:s = "(a)())()"
输出:["(a())()","(a)()()"]
class Solution {
public Set<String> set = new HashSet<>();
public int max,n,len;
public String s;
public List<String> removeInvalidParentheses(String _s) {
s = _s;
n = s.length();
int l = 0, r = 0;
char[] cs = s.toCharArray();
//选出需要删除多少个左右括号
for(char c : cs){
if(c == '(') l++;
else if(c == ')'){
if(l != 0) l--;
else r++;
}
}
len = n - l - r;
int c1 = 0,c2 = 0;
for(char c: cs){
if(c == '(') c1++;
else if(c == ')') c2++;
}
//得分最高时不能超过的值
max = Math.min(c1,c2);
dfs(0,"",l,r,0);
return new ArrayList<String>(set);
}
public void dfs(int index,String path,int l,int r, int score){
//剪枝
if(score > max || l < 0 || r < 0 || score < 0 ) return;
if(l == 0 && r == 0 && path.length() == len) set.add(path);
if(index == n) return;
char c = s.charAt(index);
if(c == '('){
dfs(index+1,path+String.valueOf(c),l,r,score+1);//拼,得分+1
dfs(index+1,path,l-1,r,score);//不拼
}else if(c == ')'){
dfs(index+1,path+String.valueOf(c),l,r,score-1);
dfs(index+1,path,l,r-1,score);
}else{
dfs(index+1,path+String.valueOf(c),l,r,score);
}
}
}
306. 累加数
累加数 是一个字符串,组成它的数字可以形成累加序列。
一个有效的 累加序列 必须 至少 包含 3 个数。除了最开始的两个数以外,序列中的每个后续数字必须是它之前两个数字之和。
给你一个只包含数字 '0'-'9' 的字符串,编写一个算法来判断给定输入是否是 累加数 。如果是,返回 true ;否则,返回 false 。
说明:累加序列里的数,除数字 0 之外,不会 以 0 开头,所以不会出现 1, 2, 03 或者 1, 02, 3 的情况。
示例 1:
输入:"112358"
输出:true
解释:累加序列为: 1, 1, 2, 3, 5, 8 。1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
示例 2:
输入:"199100199"
输出:true
解释:累加序列为: 1, 99, 100, 199。1 + 99 = 100, 99 + 100 = 199
class Solution {
String s;
int n;
public boolean isAdditiveNumber(String num) {
this.s = num;
this.n = num.length();
return dfs(0,0,0,0);
}
public boolean dfs(int index,long sum,long pre,int count){
if (index == n) {
return count >= 3;
}
long value = 0;
for(int i = index; i < n; i++){
// 除 0 以外,其他数字第一位不能为 0
if(i > index && s.charAt(index) == '0') break;
value = value * 10 + s.charAt(i) - '0';
if(count >= 2){
if(value < sum) continue;// 小的话继续向后继续拼接
else if(value > sum) break;// 大的话直接结束,再往后拼接无意义
}
//如果下次不行则返回到该层,继续,直到找到符合要求的
if (dfs(i+1,pre+value,value,count+1)) return true;
}
return false;
}
}
二十二、广度优先搜索
199. 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
class Solution {
public List<Integer> rightSideView(TreeNode root) {
LinkedList<TreeNode> queue = new LinkedList<>();
List<Integer> result = new ArrayList<>();
if(root == null) return result;
queue.add(root);
while(!queue.isEmpty()){
int size = queue.size();
for(int i = 0; i < size; i++){
TreeNode pop = queue.pop();
if(i == size-1) result.add(pop.val);
if(pop.left != null) queue.add(pop.left);
if(pop.right != null) queue.add(pop.right);
}
}
return result;
}
}
二十三、小根堆
215. 数组中的第K个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 **k** 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
class Solution {
public int findKthLargest(int[] nums, int k) {
//维护一个k 大小的 小根堆,大于队列头元素,就加入
int n = nums.length;
PriorityQueue<Integer> minHeap = new PriorityQueue<>(k,Comparator.comparingInt(a -> a));
for(int i = 0; i < k; i++){
minHeap.offer(nums[i]);
}
for(int i = k; i < n; i++){
Integer topNum = minHeap.peek();
if(topNum < nums[i]){
minHeap.poll();
minHeap.offer(nums[i]);
}
}
return minHeap.peek();
}
}
313. 超级丑数
超级丑数 是一个正整数,并满足其所有质因数都出现在质数数组 primes 中。
给你一个整数 n 和一个整数数组 primes ,返回第 n 个 超级丑数 。
题目数据保证第 n 个 超级丑数 在 32-bit 带符号整数范围内。
class Solution {
public static int nthSuperUglyNumber(int n, int[] primes) {
PriorityQueue<Integer> queue = new PriorityQueue<>();
queue.add(1);
while(n-- > 0){
int x = queue.poll();
if(n == 0) return x;
for(int num: primes){
if(num <= Integer.MAX_VALUE / x) queue.add(num * x);
//防止出现有p1*p1,p1*p2的队列,因为后面还会取出p2(因为1*p2已经加入队列了),会出现p2*p1,与之前p1*p2重复
if(x % num == 0) break;
}
}
return -1;
}
}
二十四、容斥原理
223. 矩形面积
给你 二维 平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形,请你计算并返回两个矩形覆盖的总面积。
每个矩形由其 左下 顶点和 右上 顶点坐标表示:
- 第一个矩形由其左下顶点
(ax1, ay1)和右上顶点(ax2, ay2)定义。 - 第二个矩形由其左下顶点
(bx1, by1)和右上顶点(bx2, by2)定义。

public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
int area1 = (ax2 - ax1)*(ay2 - ay1);
int area2 = (bx2 - bx1)*(by2 - by1);
int left = Math.max(ax1,bx1);
int right = Math.min(ax2,bx2);
int top = Math.min(ay2,by2);
int bottom = Math.max(ay1,by1);
int area3 = 0;
if(left < right && bottom < top){
area3 = (right-left)*(top-bottom);
}
return area1+area2-area3;
}
二十五、前缀和
二维前缀和
学习(灵茶山艾府大佬)
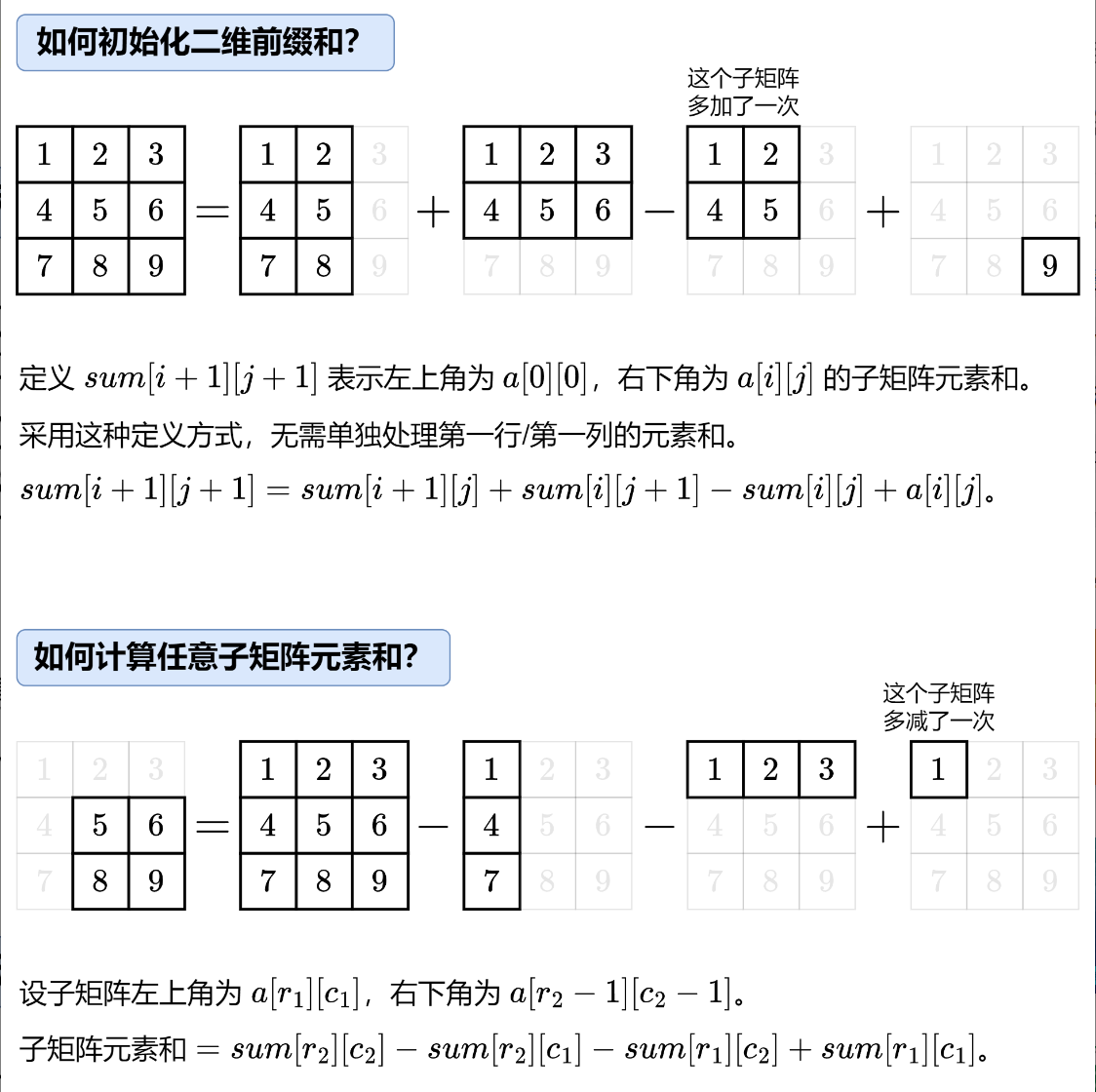
class MatrixSum {
private final int[][] sum;
public MatrixSum(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
sum = new int[m + 1][n + 1]; // 注意:如果 matrix[i][j] 范围很大,需要使用 long
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sum[i + 1][j + 1] = sum[i + 1][j] + sum[i][j + 1] - sum[i][j] + matrix[i][j];
}
}
}
// 返回左上角在 (r1,c1) 右下角在 (r2-1,c2-1) 的子矩阵元素和(类似前缀和的左闭右开)
public int query(int r1, int c1, int r2, int c2) {
return sum[r2][c2] - sum[r2][c1] - sum[r1][c2] + sum[r1][c1];
}
// 如果你不习惯左闭右开,也可以这样写
// 返回左上角在 (r1,c1) 右下角在 (r2,c2) 的子矩阵元素和
public int query2(int r1, int c1, int r2, int c2) {
return sum[r2 + 1][c2 + 1] - sum[r2 + 1][c1] - sum[r1][c2 + 1] + sum[r1][c1];
}
}
289. 生命游戏
根据 百度百科 , 生命游戏 ,简称为 生命 ,是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。
给定一个包含 m × n 个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态: 1 即为 活细胞 (live),或 0 即为 死细胞 (dead)。每个细胞与其八个相邻位置(水平,垂直,对角线)的细胞都遵循以下四条生存定律:
- 如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡;
- 如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活;
- 如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡;
- 如果死细胞周围正好有三个活细胞,则该位置死细胞复活;
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的,其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态,返回下一个状态。
示例 1:
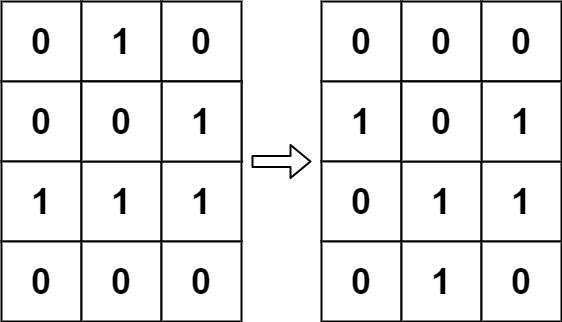
输入:board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出:[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
class Solution {
public void gameOfLife(int[][] board) {
//获取二维前缀和
int[][] preSum = getPreSum(board);
int m = board.length, n = board[0].length;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
//获取四个定点,右下角的需要额外+1,因为在求解前缀和时,(i + 1, j + 1)是(i, j)位置的前缀和,而我们需要的是(i + 1, j + 1)位置的前缀和
int r1 = Math.max(i-1,0);
int c1 = Math.max(j-1,0);
int r2 = Math.min(i+2,m);
int c2 = Math.min(j+2,n);
int sum = searchPre(preSum,r1,c1,r2,c2);
if(board[i][j] == 1){//活细胞
if(sum-1 < 2 || sum - 1 > 3) board[i][j] = 0;
}else{//死细胞
if(sum == 3) board[i][j] = 1;
}
}
}
}
public int searchPre(int[][] sum, int r1,int c1,int r2,int c2){
return sum[r2][c2] - sum[r1][c2]-sum[r2][c1] + sum[r1][c1];
}
public int[][] getPreSum(int[][] board){
int m = board.length;
int n = board[0].length;
int[][] sum = new int[m+1][n+1];
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
sum[i+1][j+1] = sum[i][j+1]+sum[i+1][j]-sum[i][j]+board[i][j];
}
}
return sum;
}
}


