力扣题解(1-150)
原文链接:https://gaoyubo.cn/blogs/3ecd1562.html
一、双指针
27. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
package leetCodePractice;
/**
* @Date 2023/9/11 17:56
* @Author 郜宇博
*/
public class Solution27 {
public static int removeElement(int[] nums, int val) {
if (nums.length == 0 || nums == null) return 0;
int firstIndex = 0;
int secondIndex = nums.length-1;
while (firstIndex <= secondIndex){
if (nums[firstIndex] == val){
swap(nums,firstIndex,secondIndex--);
}else {
firstIndex++;
}
}
return secondIndex + 1;
}
private static void swap(int[] nums, int firstIndex, int secondIndex) {
int temp;
temp = nums[firstIndex];
nums[firstIndex] = nums[secondIndex];
nums[secondIndex] = temp;
}
}
31. 下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
- 例如,
arr = [1,2,3],以下这些都可以视作arr的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1]。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
- 例如,
arr = [1,2,3]的下一个排列是[1,3,2]。 - 类似地,
arr = [2,3,1]的下一个排列是[3,1,2]。 - 而
arr = [3,2,1]的下一个排列是[1,2,3],因为[3,2,1]不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
两种方法1.
- 先倒序遍历数组, 找到第一个 nums[i] (前一个数比后一个数小的位置) (即nums[i] < nums[i+1]);
- 这个时候我们不能直接把后一个数nums[i+1] 跟前一个数nums[i]交换就完事了; 还应该从nums[i+1]-->数组末尾这一段的数据中 找出最优的那个值( 如何最优? 即比nums[i]稍微大那么一丢丢的数, 也就是
nums[i+1]-->数组末尾中, 比nums[i]大的数中最小的那个值) - 找到之后, 跟num[i]交换, 这还不算是下一个排列, num[i]后面的数值还不够小, 所以还应当进升序排列
public static void nextPermutation(int[] nums) {
for (int i = nums.length-1; i > 0; i--){
if (nums[i-1] < nums[i]){
//找到一个最小的与i-1交换
int minNum = Integer.MAX_VALUE;
int minIndex = 0;
for (int j = i; j < nums.length;j++){
if (nums[j] < minNum && nums[j] > nums[i-1]){
minNum = nums[j];
minIndex = j;
}
}
int temp = nums[minIndex];
nums[minIndex] = nums[i-1];
nums[i-1] = temp;
Arrays.sort(nums,i,nums.length);
return;
}
}
Arrays.sort(nums);
}
方法2.
public static void nextPermutation1(int[] nums) {
int i = nums.length-2;
while (i >= 0){
if (nums[i+1] > nums[i]) break;
i--;
}
if (i >= 0){
for (int j = nums.length-1;j >=0; j--){
if (nums[j] > nums[i]) {
swap(nums,i,j);
break;
}
}
}
reverseArr(nums,i+1,nums.length-1);
}
public static void swap(int[] nums,int index1,int index2){
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
public static void reverseArr(int[] nums,int start,int end){
while (start < end){
swap(nums,start++,end--);
}
}
56. 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
public int[][] merge(int[][] intervals) {
if (intervals.length == 1) return intervals;
List<int[] > list =new ArrayList<>();
Arrays.sort(intervals, Comparator.comparingInt(interval -> interval[0]));
int left = intervals[0][0],right = intervals[0][1];
for (int i = 1; i < intervals.length; i++){
if (intervals[i][0] <= right){
right = Math.max(right,intervals[i][1]);
}else {
list.add(new int[]{left,right});
left = intervals[i][0];
right = intervals[i][1];
}
}
list.add(new int[]{left,right});
return list.toArray(new int[list.size()][]);
}
58. 最后一个单词的长度
给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。
单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。
示例 1:
输入:s = "Hello World"
输出:5
解释:最后一个单词是“World”,长度为5。
示例 2:
输入:s = " fly me to the moon "
输出:4
解释:最后一个单词是“moon”,长度为4。
示例 3:
输入:s = "luffy is still joyboy"
输出:6
解释:最后一个单词是长度为6的“joyboy”。
package leetCodePractice;
/**
* @Date 2023/9/11 19:14
* @Author 郜宇博
*/
public class Solution58 {
public int lengthOfLastWord(String s) {
String[] s1 = s.split(" ");
return s1[s1.length-1].length();
}
public int lengthOfLastWord2(String s) {
//存在为空格 则去除
char[] charArray = s.toCharArray();
int end = charArray.length-1;
while (end >=0 && charArray[end] == ' '){
end--;
}
int start = end;
while (start >= 0 && charArray[start] != ' '){
start--;
}
return end - start;
}
}
61. 旋转链表
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
示例 1:
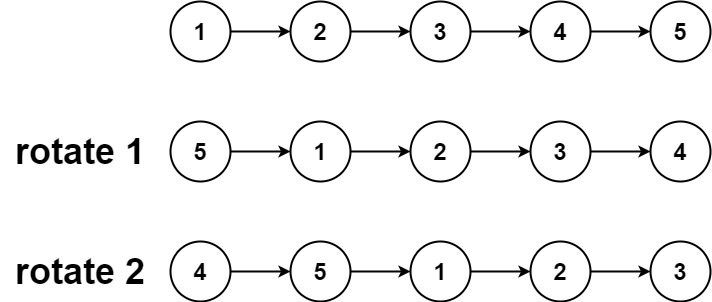
输入:head = [1,2,3,4,5], k = 2
输出:[4,5,1,2,3]
示例 2:
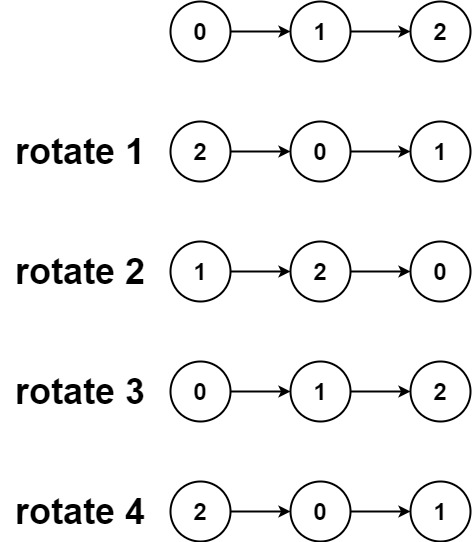
输入:head = [0,1,2], k = 4
输出:[2,0,1]
/**
先将给定的链表连接成环,然后将指定位置断开。
具体代码中,我们首先计算出链表的长度 nnn,并找到该链表的末尾节点,将其与头节点相连。
这样就得到了闭合为环的链表。
然后我们找到新链表的最后一个节点(即原链表的第 (n−1)−(k mod n)(n - 1) - (k \bmod n)(n−1)−(kmodn) 个节点),将当前闭合为环的链表断开,
*/
public ListNode rotateRight(ListNode head, int k) {
if (k == 0 || head == null) return head;
int length = 1;
ListNode cur = head;
while (cur.next != null){
length++;
cur = cur.next;
}
cur.next = head;
int step = length - (k % length);
while (step-- >0){
cur = cur.next;
}
ListNode newHead = cur.next;
cur.next = null;
return newHead;
}
75. 颜色分类
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1]
输出:[0,1,2]
public void sortColors(int[] nums) {
int p0 = 0, p1 = 0;
for (int i = 0 ; i < nums.length; i++){
if (nums[i] == 0){
int temp = nums[i];
nums[i] = nums[p0];
nums[p0] = temp;
if (p0 < p1){
temp = nums[i];
nums[i] = nums[p1];
nums[p1] = temp;
}
p1++;
p0++;
}else if (nums[i] == 1){
int temp = nums[i];
nums[i] = nums[p1];
nums[p1] = temp;
p1++;
}
}
}
80. 删除有序数组中的重复项 II
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 1:
输入:nums = [1,1,1,2,2,3]
输出:5, nums = [1,1,2,2,3]
解释:函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3。 不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,1,2,3,3]
输出:7, nums = [0,0,1,1,2,3,3]
解释:函数应返回新长度 length = 7, 并且原数组的前五个元素被修改为 0, 0, 1, 1, 2, 3, 3。不需要考虑数组中超出新长度后面的元素。
思路
假设有如下样例
[1,1,1,1,1,1,2,2,2,2,2,2,3]
- 首先我们先让前 2 位直接保留,得到 1,1
- 对后面的每一位进行继续遍历,能够保留的前提是与当前位置的前面 k 个元素不同(答案中的
第一个 1),因此我们会跳过剩余的 1,将第一个 2 追加,得到 1,1,2 - 继续这个过程,这时候是和答案中的
第 2 个 1进行对比,因此可以得到 1,1,2,2 - 这时候和答案中的
第 1 个 2比较,只有与其不同的元素能追加到答案,因此剩余的 2 被跳过,3 被追加到答案:1,1,2,2,3
83. 删除排序链表中的重复元素
给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。
示例 1:
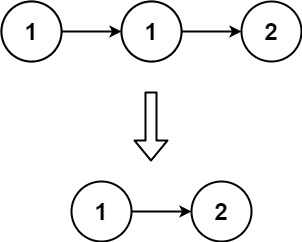
输入:head = [1,1,2]
输出:[1,2]
示例 2:
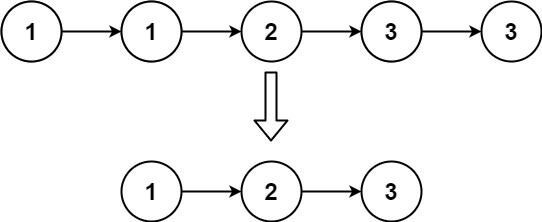
输入:head = [1,1,2,3,3]
输出:[1,2,3]
提示:
- 链表中节点数目在范围
[0, 300]内 -100 <= Node.val <= 100- 题目数据保证链表已经按升序 排列
class Solution {
public ListNode deleteDuplicates(ListNode head) {
if (head == null || head.next == null) return head;
ListNode tempNode = head.next;
ListNode pre = head;
while (tempNode != null){
if (tempNode.val == pre.val){
//重复了,需要删除
pre.next = tempNode.next;
}else{
pre = tempNode;
}
tempNode = tempNode.next;
}
return head;
}
}
86. 分隔链表
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。
示例 1:
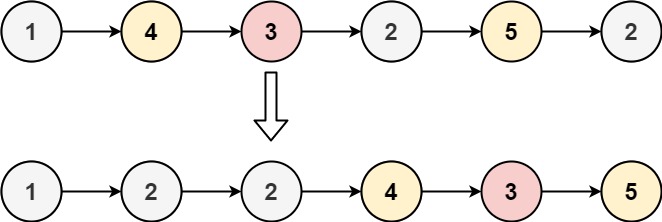
输入:head = [1,4,3,2,5,2], x = 3
输出:[1,2,2,4,3,5]
示例 2:
输入:head = [2,1], x = 2
输出:[1,2]
class Solution {
public ListNode partition(ListNode head, int x) {
if(head == null || head.next == null) return head;
//维护两个链表,大于等于和小于,结束遍历后,将小于的链表后衔接大于等于链表即可
ListNode lList = new ListNode();
ListNode beList = new ListNode();
ListNode curl = lList;
ListNode curbe = beList;
while(head != null){
if(head.val < x){
curl.next = head;
curl = curl.next;
}else{
curbe.next = head;
curbe = curbe.next;
}
head = head.next;
}
curbe.next = null;
curl.next = beList.next;
return lList.next;
}
}
88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[j] <= 109
进阶:你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
package leetCodePractice;
import java.util.Arrays;
/**
* @Date 2023/9/13 11:36
* @Author 郜宇博
*/
public class Solution88 {
public static void main(String[] args) {
int[] n1 = new int[]{0};
int[] n2 = new int[]{1};
merge2(n1,0,n2,1);
}
public static void merge(int[] nums1, int m, int[] nums2, int n) {
int[] nums1Save = new int[m];
System.arraycopy(nums1, 0, nums1Save, 0, m);
int index1 = 0,index2 = 0;
int sortIndex = 0;
while (sortIndex < m + n && index1 < m && index2 < n){
if (nums1Save[index1] < nums2[index2]){
nums1[sortIndex++] = nums1Save[index1++];
}else {
nums1[sortIndex++] = nums2[index2++];
}
}
//num2元素还有剩余
if (index1 == m && index2 != n){
for (int i = index2; i < n; i++){
nums1[m+index2] = nums2[i];
index2++;
}
}else if (index1 != m && index2 == n){
//num1还有剩余
for (int i = index1; i < m; i++){
nums1[n+index1] = nums1Save[i];
index1++;
}
}
}
public static void merge2(int[] nums1, int m, int[] nums2, int n){
int num1Index = m-1;
int mergeIndex = nums1.length-1;
int num2Index = n-1;
//遍历两个数组,比较元素,谁大谁放数组后面
while (mergeIndex >= 0 && num2Index >= 0 && num1Index >= 0){
if (nums2[num2Index] >= nums1[num1Index] ){
nums1[mergeIndex] = nums2[num2Index--];
}else if ( nums1[num1Index] > nums2[num2Index]){
nums1[mergeIndex] = nums1[num1Index--];
}
mergeIndex--;
}
//num1还有剩余,不能使用num1Index判断,因为num1的长度有可能为0
if (num2Index >= 0){
System.arraycopy(nums2, 0, nums1, 0, num2Index);
}
}
}
125. 验证回文串
如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。
字母和数字都属于字母数字字符。
给你一个字符串 s,如果它是 回文串 ,返回 true ;否则,返回 false 。
示例 1:
输入: s = "A man, a plan, a canal: Panama"
输出:true
解释:"amanaplanacanalpanama" 是回文串。
示例 2:
输入:s = "race a car"
输出:false
解释:"raceacar" 不是回文串。
示例 3:
输入:s = " "
输出:true
解释:在移除非字母数字字符之后,s 是一个空字符串 "" 。
由于空字符串正着反着读都一样,所以是回文串。
提示:
1 <= s.length <= 2 * 105s仅由可打印的 ASCII 字符组成
class Solution {
public static boolean isPalindrome(String s) {
if (s.isEmpty() || s.length() == 1) return true;
int left = 0;
int right = s.length()-1;
//
s = s.toUpperCase();
while (left <= right){
while (left <= right && !testChar(s.charAt(left))){
//不属于字母表,跳过
left++;
}
while (left <= right && !testChar(s.charAt(right))){
//不属于字母表,跳过
right--;
}
if(left > right){
break;
}
//找到了字母,进行对比
if (s.charAt(left) == s.charAt(right)) {
left++;
right--;
}else{
return false;
}
}
return true;
}
//不属于字母
public static boolean testChar(char c){
return ('A'<=c && 'Z' >= c) || '0' <= c && '9'>= c;
}
}
141. 环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
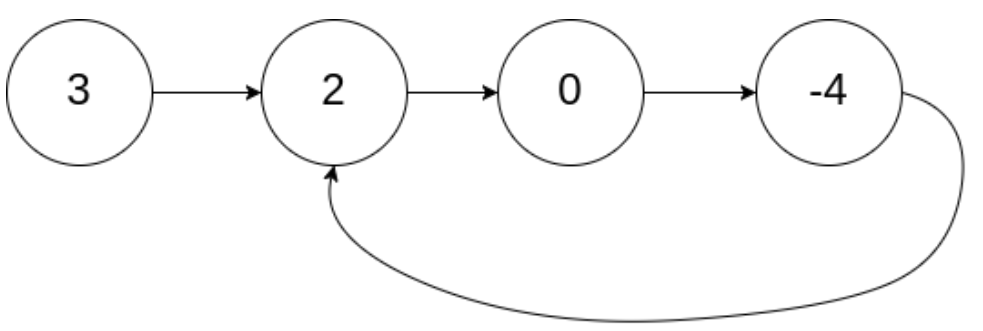
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
public class Solution {
public boolean hasCycle(ListNode head) {
if(head == null) return false;
ListNode slow = head;
ListNode fast = head;
while(fast.next != null && fast.next.next!=null){
slow = slow.next;
fast = fast.next.next;
if(slow == fast) return true;
}
return false;
}
}
142. 环形链表 II
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
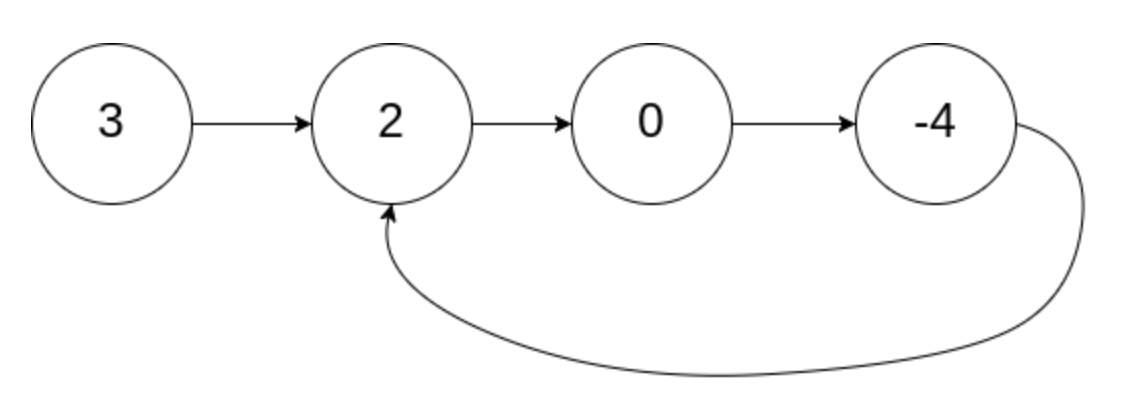
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
public class Solution {
public ListNode detectCycle(ListNode head) {
if(head == null) return null;
ListNode slow = head, fast = head;
while(fast.next != null && fast.next.next != null){
slow = slow.next;
fast = fast.next.next;
if(slow == fast){
fast = head;
while(slow != fast){
slow = slow.next;
fast = fast.next;
}
return fast;
}
}
return null;
}
}
143. 重排链表
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:
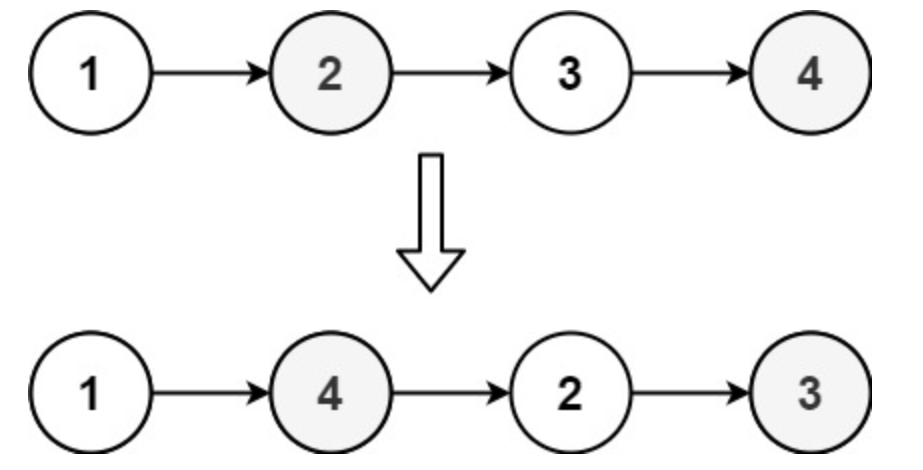
输入:head = [1,2,3,4]
输出:[1,4,2,3]
class Solution {
public void reorderList(ListNode head) {
ListNode slow = head, fast = head,pre = null,cur = head,next = null;
//1.寻找中间节点
while(fast.next != null && fast.next.next != null){
slow = slow.next;
fast = fast.next.next;
}
//2.反转链表
while(slow != null){
next = slow.next;
slow.next = pre;
pre = slow;
slow = next;
}
//3.合并链表
ListNode leftNext = head;
ListNode rightNext = pre;
while(cur != null && pre != null){
leftNext = cur.next;
rightNext = pre.next;
cur.next = pre;
pre.next = leftNext;
cur = leftNext;
pre = rightNext;
}
}
}
二、二分法
35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
package leetCodePractice;
/**
* @Date 2023/9/11 18:41
* @Author 郜宇博
*/
public class Solution35 {
public static int searchInsert(int[] nums, int target) {
int firstIndex = 0;
int secondIndex = nums.length-1;
while (firstIndex <= secondIndex){
if (nums[firstIndex] >= target) return firstIndex;
if (nums[secondIndex] == target) return secondIndex;
if (nums[secondIndex] < target) return secondIndex+1;
firstIndex++;
secondIndex--;
}
return firstIndex;
}
public static int searchInsert2(int[] nums, int target) {
int left = 0;
int right = nums.length-1;
int mid = (left+right)/2;
while (left <= right){
mid = (left+right)/2;
if (nums[mid] == target) return mid;
if (nums[mid] < target){
left = mid + 1;
}else {
right = mid - 1;
}
}
return left;
}
}
33. 搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
public int search(int[] nums, int target) {
//二分法查找,如果查找的目标比数组最左还小,说明在右边,left = mid +1
int left = 0, right = nums.length -1;
while (left < right){
int mid = left + (( right - left) >> 1);
if (nums[mid] == target) return mid;
//left - mid是顺序区间
if (nums[left ] < nums[mid]){
//在mid左边
if (target >= nums[left] && target < nums[mid]){
right = mid - 1;
}else {
//在mid右边
left = mid + 1;
}
}else {//mid - right是顺序区间
if (target <= nums[right] && target > nums[mid]){
left = mid + 1;
}else {
right = mid -1;
}
}
}
return -1;
}
34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
public int[] searchRange(int[] nums, int target) {
if (nums.length != 0){
int left = 0;
int right = nums.length-1;
while (left <= right){
int mid = left + ((right - left) >> 1);
if (target == nums[mid]){
int start = mid,end = mid;
while (start >= 0 && nums[start] == nums[mid]){
start--;
}
while ( end < nums.length && nums[end] == nums[mid]){
end++;
}
return new int[]{start+1,end-1};
} else if (target < nums[mid]){
right = mid-1;
}else {
left = mid + 1;
}
}
}
return new int[]{-1,-1};
}
69. x 的平方根
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
package leetCodePractice;
/**
* @Date 2023/9/13 10:46
* @Author 郜宇博
*/
public class Solution69 {
public static int mySqrt(int x) {
if ((long) x == 0) return 0;
if ((long) x < 4) return 1;
for (long i = 2; i <= (long) x / 2; i++){
if (i * i == (long) x) return (int) i;
if(i * i > (long) x) return (int) (i - 1);
}
return -1;
}
public static int mySqrt1(int x){
if ( x == 0) return 0;
if ((x < 4)) return 1;
int left = 0;
int right = x / 2;
while (left <= right){
int mid = (left + right) >> 1;
if (mid == x / mid){
return mid;
}
if (mid > x / mid){
right = mid - 1;
}else {
left = mid + 1;
}
}
return left -1;
}
}
74. 搜索二维矩阵
给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
示例 1:
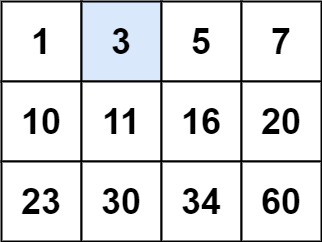
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出:true
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length;
int n = matrix[0].length;
int row = -1;
for (int i = 0; i < m; i++){
if (matrix[i][n-1] >= target){
row = i;
break;
}
}
if (row == -1) return false;
int left = 0, right = n-1;
while (left <= right){
int mid = left + ((right-left) >> 1);
if (matrix[row][mid] == target){
return true;
}else if (target > matrix[row][mid]){
left = mid + 1;
}else{
right = mid - 1;
}
}
return false;
}
81. 搜索旋转排序数组 II
已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。
给你 旋转后 的数组 nums 和一个整数 target ,请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false 。
你必须尽可能减少整个操作步骤。
示例 1:
输入:nums = [2,5,6,0,0,1,2], target = 0
输出:true
示例 2:
输入:nums = [2,5,6,0,0,1,2], target = 3
输出:false
思路:与最左边的数比较,如果大于则说明左侧有序,反之右侧有序
如果相等则left++,更换一个比较
class Solution {
public boolean search(int[] nums, int target) {
int left = 0,right = nums.length-1;
while(left <= right){
int mid = left + ( (right - left ) >> 1);
if(nums[mid] == target) return true;
//左边是顺序区间:[left,mid)有序
if(nums[mid] > nums[left]){
//在mid左侧
if(target >= nums[left] && target < nums[mid]){
right = mid - 1;
}else{
left = mid + 1;
}
}else if(nums[mid] < nums[left]){
if(target <= nums[right] && target > nums[mid]){
left = mid + 1;
}else{
right = mid - 1;
}
}else{
//无法判断,只能换一个left
left++;
}
}
return false;
}
}
三、数学(取余,二进,异或,进制)
2. 两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
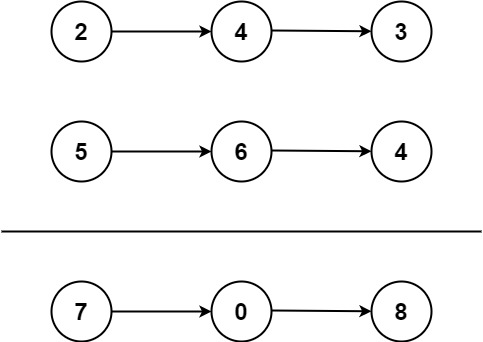
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
int carry = 0,sumNoCarry;
ListNode root = new ListNode(0);
ListNode cur = root;
while (l1 != null || l2 != null){
int x = l1 == null?0: l1.val;
int y = l2 == null?0: l2.val;;
sumNoCarry = carry;
sumNoCarry += x + y;
carry = sumNoCarry / 10;
cur.next = new ListNode(sumNoCarry % 10);
cur = cur.next;
if (l1 != null) l1 = l1.next;
if (l2 != null) l2 = l2.next;
}
if (carry != 0){
cur.next = new ListNode(carry);
}
return root.next;
}
7. 整数反转
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:
输入:x = 123
输出:321
示例 2:
输入:x = -123
输出:-321
示例 3:
输入:x = 120
输出:21
class Solution {
public static int reverse(int x) {
boolean sign = x > 0;
x = Math.abs(x);
int result = 0,a;
while (x > 0){
a = x % 10;
x /= 10;
if ((result == Integer.MAX_VALUE/10 && a < Integer.MAX_VALUE % 10) || result < Integer.MAX_VALUE/10){
result = result * 10 + a;
}else {
return 0;
}
}
return sign?result:result*-1;
}
}
66. 加一
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
输入:digits = [1,2,3]
输出:[1,2,4]
解释:输入数组表示数字 123。
示例 2:
输入:digits = [4,3,2,1]
输出:[4,3,2,2]
解释:输入数组表示数字 4321。
示例 3:
输入:digits = [0]
输出:[1]
class Solution {
public static int[] plusOne(int[] digits){
//元素值< 9 则+1,=9则变为0
for (int i = digits.length-1; i >=0; i--){
digits[i] = (digits[i] +1) % 10;
//有一位不为9,可以退出了
if (digits[i] != 0){
return digits;
}
}
//一直进位到了d[0]位置,需要新建数组
digits = new int[digits.length+1];
digits[0] = 1;
//数组创建默认元素为0,因此后面不需要赋值
return digits;
}
}
67. 二进制求和
给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。
示例 1:
输入:a = "11", b = "1"
输出:"100"
示例 2:
输入:a = "1010", b = "1011"
输出:"10101"
package leetCodePractice;
/**
* @Date 2023/9/11 20:58
* @Author 郜宇博
*/
public class Solution67 {
public String addBinary(String a, String b) {
/*
1010
1011
0001
1 1
*/
StringBuilder stringBuilder = new StringBuilder();
//int up = 0;
int sum = 0;
for (int i = a.length()-1, j = b.length()-1; i>=0 || j >=0;i--,j--){
if (i >=0){
sum += a.charAt(i) - '0';
}
if (j >= 0){
sum += b.charAt(j) - '0';
}
stringBuilder.append(sum % 2);
//需要计算进位,只有和为2需要进位
sum /= 2;
}
if (sum != 0){
stringBuilder.append("1");
}
return stringBuilder.reverse().toString();
}
}
136. 只出现一次的数字
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1]
输出:1
示例 2 :
输入:nums = [4,1,2,1,2]
输出:4
示例 3 :
输入:nums = [1]
输出:1
提示:
1 <= nums.length <= 3 * 104-3 * 104 <= nums[i] <= 3 * 104- 除了某个元素只出现一次以外,其余每个元素均出现两次。
public static int singleNumber(int[] nums) {
//异或本身会等于0
if (nums.length == 1) return nums[0];
int ans = nums[0];
for (int i = 1; i < nums.length; i++){
ans ^= nums[i];
}
return ans;
}
137. 只出现一次的数字 II
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
示例 1:
输入:nums = [2,2,3,2]
输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99]
输出:99
提示:
1 <= nums.length <= 3 * 104-231 <= nums[i] <= 231 - 1nums中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次
题解
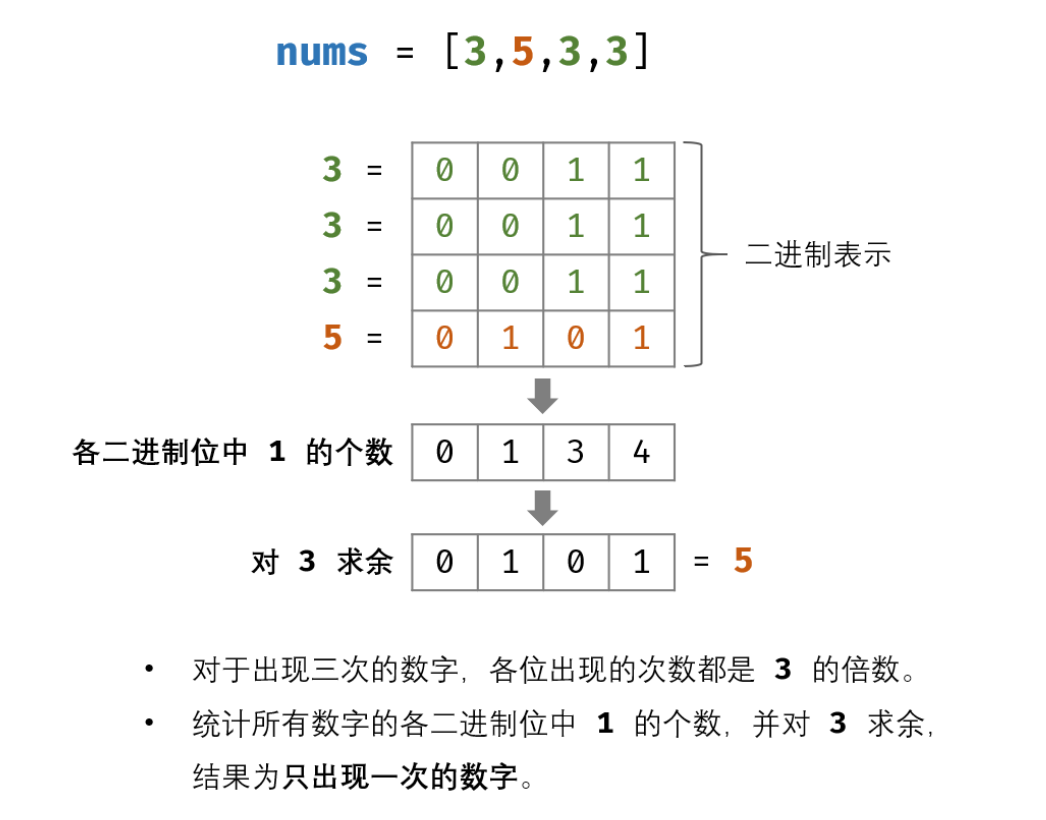
class Solution {
public int singleNumber(int[] nums) {
int[] count = new int[32];
for(int num: nums){
for(int i = 0; i < 32; i++){
count[i] += num & 1;
num >>>= 1;
}
}
int res = 0, m = 3;
for(int i = 31; i >= 0; i--) {
res <<= 1;
res |= count[i] % 3;
}
return res;
}
}
149. 直线上最多的点数
给你一个数组 points ,其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
示例 1:
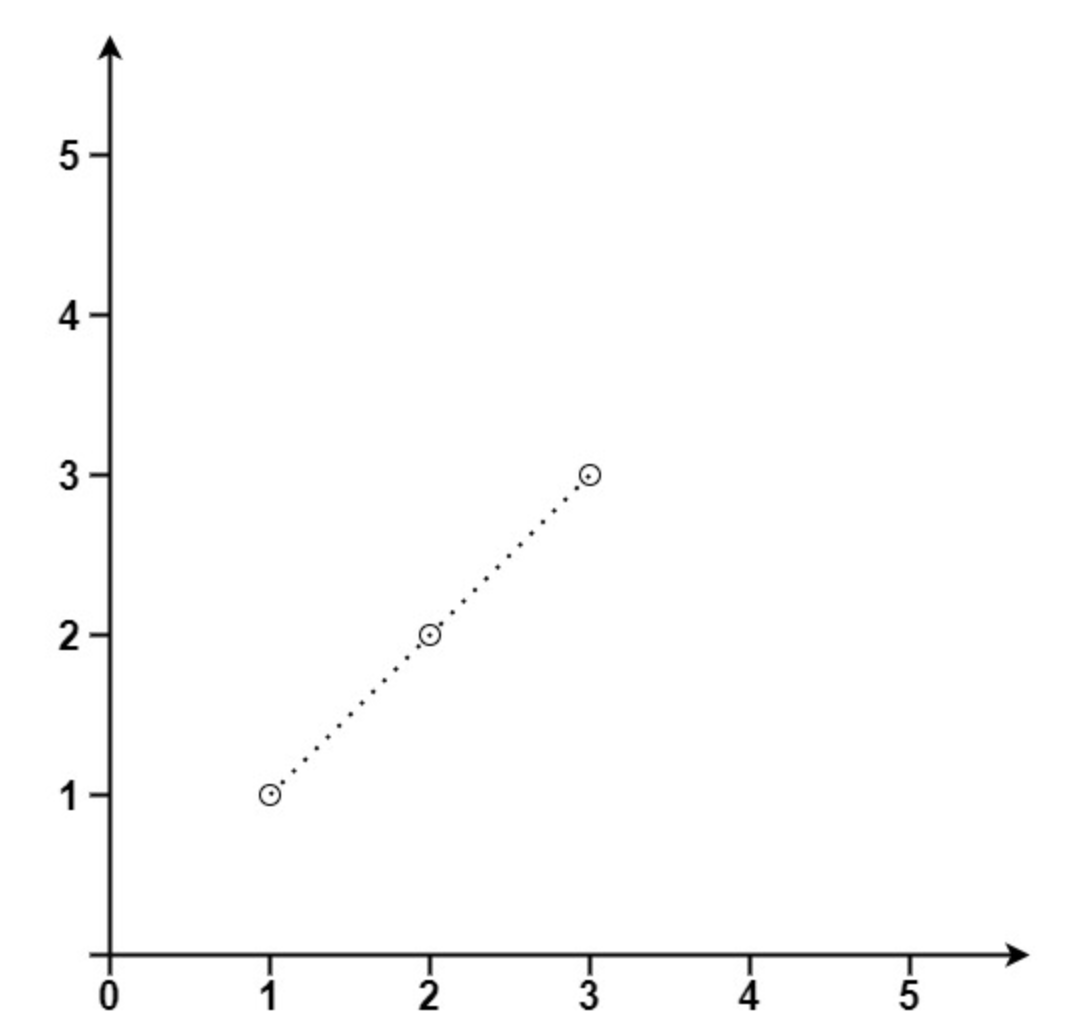
输入:points = [[1,1],[2,2],[3,3]]
输出:3
示例 2:
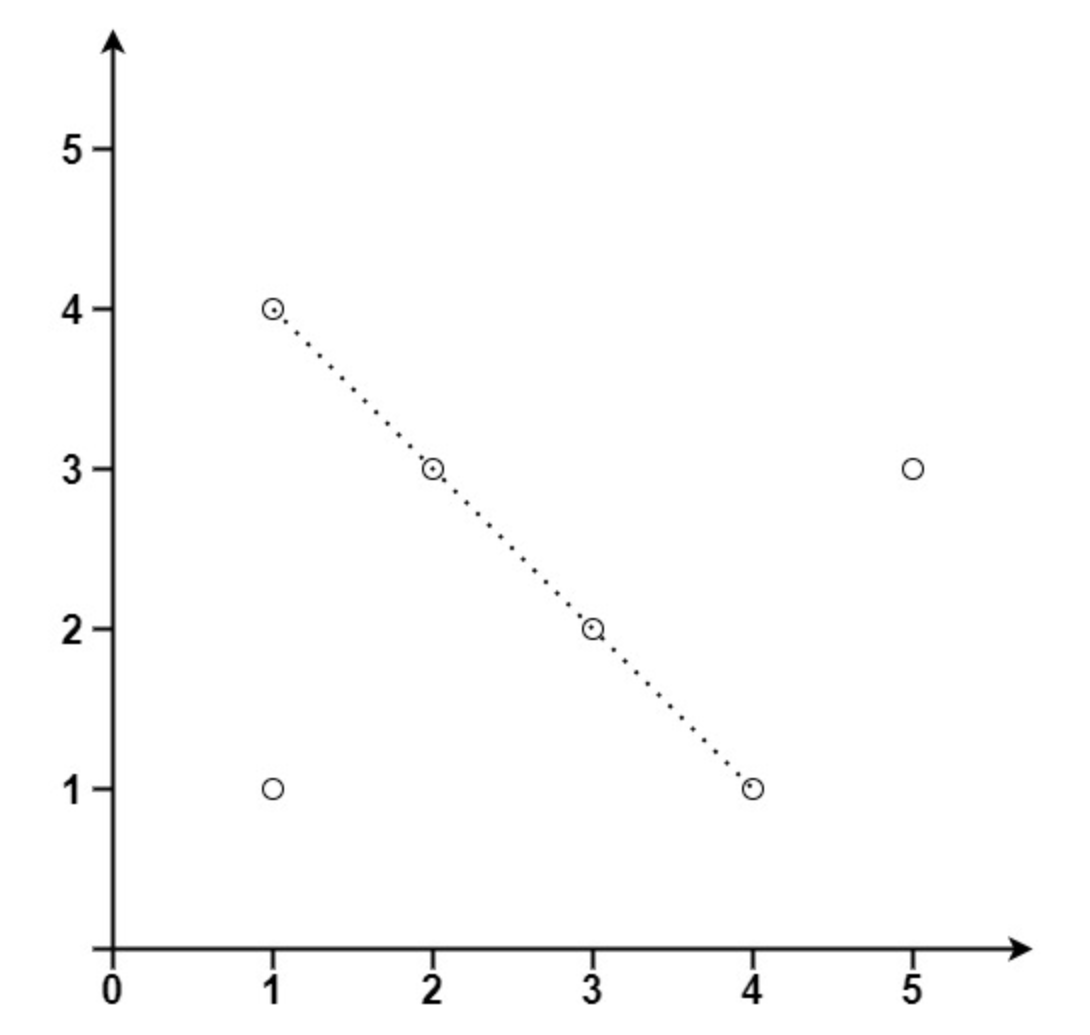
输入:points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出:4
思路:先枚举两条点(确定一条线),然后检查其余点是否落在该线中。
class Solution {
public int maxPoints(int[][] points) {
int n = points.length;
int result = 1;
for(int i = 0; i < n; i++){
int[] x = points[i];
for(int j = i + 1; j < n; j++){
int[] y = points[j];
int temp = 2;
for(int k = j + 1; k < n; k++){
int[] z = points[k];
//交叉相乘,防止除出现精度问题
int xyK = (x[1]-y[1]) * (y[0]-z[0]);
int yzK = (y[1]-z[1]) * (x[0]-y[0]);
if(xyK == yzK) temp++;
}
result = Math.max(result,temp);
}
}
return result;
}
}
四、分治法
108. 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:
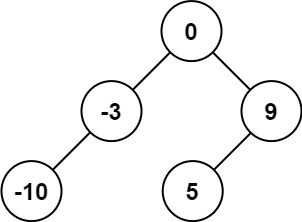
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
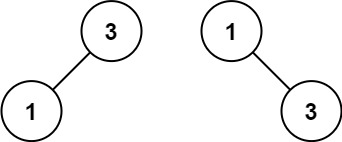
输入:nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
/**
* @Date 2023/9/13 18:31
* @Author 郜宇博
*/
public class Solution108 {
public TreeNode sortedArrayToBST(int[] nums) {
return DFS(0,nums.length-1,nums);
}
public static TreeNode DFS(int left, int right, int[] nums){
//出口
if (left > right){
return null;
}
int mid = left + (right - left) >> 1;
int val = nums[mid];
TreeNode curRoot = new TreeNode(val);
curRoot.left = DFS(left,mid-1,nums);
curRoot.right = DFS(mid+1,right,nums);
return curRoot;
}
}
109. 有序链表转换二叉搜索树
给定一个单链表的头节点 head ,其中的元素 按升序排序 ,将其转换为高度平衡的二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。
示例 1:
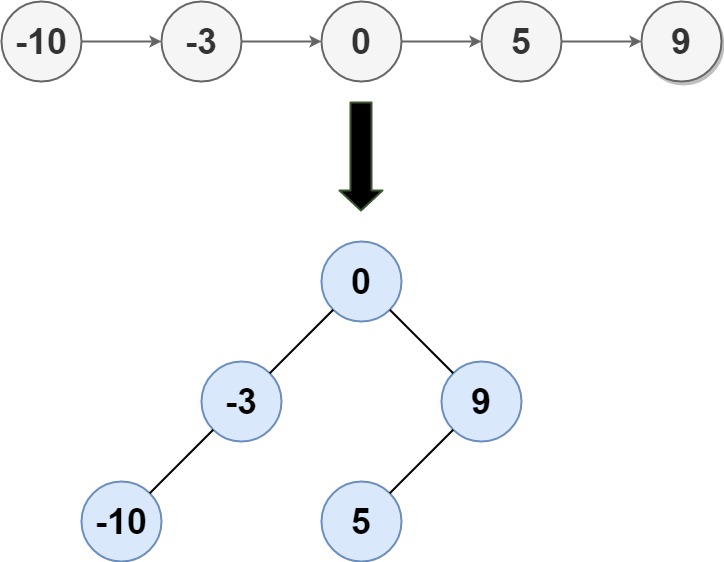
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0,-3,9,-10,null,5],它表示所示的高度平衡的二叉搜索树。
示例 2:
输入: head = []
输出: []
class Solution {
ListNode head;
public TreeNode sortedListToBST(ListNode head) {
this.head = head;
int n = 0;
ListNode cur = head;
while(cur != null && n++ >= 0) cur = cur.next;
return process(0,n-1);
}
public TreeNode process(int start, int end){
if(start >end) return null;
int mid = (start + end) >> 1;
TreeNode left = process(start,mid-1);
TreeNode root = new TreeNode(head.val);
//此时head已经走到了中间,因为构建完了左子树
head = head.next;
root.left = left;
root.right = process(mid +1, end);
return root;
}
}
五、摩尔投票法 求众数
六、Hash存储
49. 字母异位词分组
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
示例 2:
输入: strs = [""]
输出: [[""]]
示例 3:
输入: strs = ["a"]
输出: [["a"]]
public List<List<String>> groupAnagrams(String[] strs) {
//key为重新将字符串中字符排序的字符串
HashMap<String,List<String>> map = new HashMap<>();
for (String str:strs){
char[] charArray = str.toCharArray();
Arrays.sort( charArray);
String key = Arrays.toString(charArray);
List<String> stringList = map.getOrDefault(key, new ArrayList<>());
stringList.add(str);
map.put(key,stringList);
}
return new ArrayList<>(map.values());
}
105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
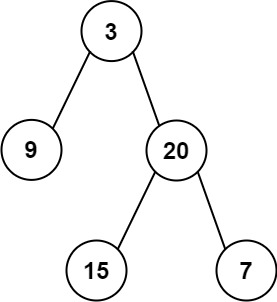
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
public TreeNode buildTree(int[] preorder, int[] inorder) {
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < preorder.length; i++) {
map.put(inorder[i], i);
}
return process(preorder,inorder,0,preorder.length-1,0,preorder.length-1,map);
}
public TreeNode process(int[] preorder,int[] inorder, int preLeft,int preRight,int inLeft,int inRight,HashMap<Integer,Integer> map){
//出口
if(preLeft > preRight) return null;
//获取中序遍历根索引
int inRootIndex = map.get(preorder[preLeft]);
TreeNode root = new TreeNode(preorder[preLeft]);
//左子树节点数量
int leftNodeCount = inRootIndex - inLeft;
//构建左子树
root.left = process(preorder,inorder,preLeft+1,preLeft+leftNodeCount,inLeft,inRootIndex-1,map);
//构建右子树
root.right = process(preorder,inorder,preLeft+leftNodeCount+1,preRight,inRootIndex+1,inRight,map);
return root;
}
106. 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
HashMap<Integer,Integer> map = new HashMap<>();
int n = inorder.length;
// 将中序遍历放到map中
for (int i = 0; i < n; ++i) {
map.put(inorder[i], i);
}
return process(postorder,inorder,0,n-1,0,n-1,map);
}
public TreeNode process(int[] postorder,int[] inorder, int inLeft, int inRight,int posLeft,int posRight,HashMap<Integer,Integer> map){
if(posLeft > posRight){
return null;
}
int inRootIndex = map.get(postorder[posRight]);
int leftNodeCount = inRootIndex - inLeft;
TreeNode root = new TreeNode(postorder[posRight]);
root.left = process(postorder,inorder,inLeft,inRootIndex - 1,posLeft,posLeft+leftNodeCount-1,map);
root.right = process(postorder,inorder,inRootIndex+1,inRight,posLeft+leftNodeCount,posRight-1,map);
return root;
}
}
138. 随机链表的复制
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示Node.val的整数。random_index:随机指针指向的节点索引(范围从0到n-1);如果不指向任何节点,则为null。
你的代码 只 接受原链表的头节点 head 作为传入参数。
示例 1:

输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
class Solution {
public Node copyRandomList(Node head) {
Node oldHead = head;
HashMap<Node,Node> map = new HashMap<>();
while(oldHead != null){
//创建映射关系:old-->new
map.put(oldHead,new Node(oldHead.val));
oldHead = oldHead.next;
}
oldHead = head;
while(oldHead != null){
//创建连接关系
map.get(oldHead).next = map.get(oldHead.next);
map.get(oldHead).random = map.get(oldHead.random);
oldHead = oldHead.next;
}
return map.get(head);
}
}
七、队列 <--->栈
150. 逆波兰表达式求值
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。 - 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
class Solution {
public static int evalRPN(String[] tokens) {
LinkedList<Integer> stack = new LinkedList<>();
for(String str: tokens){
int num = isNum(str);
if(num != 1000){
stack.push(num);
}else{
int num1 = stack.pop();
int num2 = stack.pop();
switch (str) {
case "+":
stack.push(num2 + num1);
break;
case "-":
stack.push(num2 - num1);
break;
case "*":
stack.push(num2 * num1);
break;
default:
stack.push(num2 / num1);
break;
}
}
}
return stack.pop();
}
public static int isNum(String str){
if(!(str.equals("+") || str.equals("-") ||str.equals("*") || str.equals("/")) ){
return Integer.parseInt(str);
}
return 1000;
}
}
八、博弈论
九、动态规划
普通DP
53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
public int maxSubArray(int[] nums) {
//dp[i] -->以nums[i]为结尾的最大子数组和
int[] dp = new int[nums.length];
dp[0] = nums[0];
int max = dp[0];
for (int i = 1; i < nums.length;i++){
//如果上一个元素为结尾的最大子数组和 < 0,下次就不用加了
dp[i] = dp[i-1] > 0? nums[i]+dp[i-1]:nums[i];
max = Math.max(max,dp[i]);
}
return Math.max(max,dp[nums.length-1]);
}
62. 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
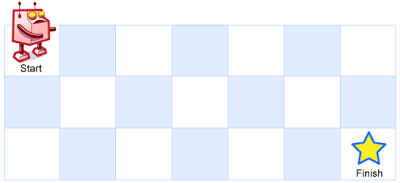
输入:m = 3, n = 7
输出:28
public int uniquePaths(int m, int n) {
if (m == 1 || n == 1) return 1;
int[] dp = new int[n];
Arrays.fill(dp,1);
for (int i = 0; i < m-1; i++){
for (int j = n-2; j >= 0; j--){
dp[j] += dp[j+1];
}
}
return dp[0];
}
63. 不同路径 II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[] dp = new int[n+1];
dp[n-1] = 1;
for (int i = m-1; i >= 0; i--){
for (int j = n-1; j >= 0; j--){
if (obstacleGrid[i][j] == 1){
dp[j] = 0;
}else {
dp[j] += dp[j+1];
}
}
}
return dp[0];
}
64. 最小路径和
给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
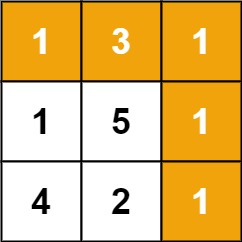
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
public static int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[] dp = new int[n+1];
dp[n-1] = grid[m-1][n-1];
dp[n] = Integer.MAX_VALUE;
for (int i = n-2; i >= 0; i--){
dp[i] = dp[i +1] + grid[m-1][i];
}
for (int i = m - 2; i >= 0; i--){
for (int j = n - 1; j >= 0; j--){
dp[j] = Math.min(dp[j+1],dp[j]) + grid[i][j];
}
}
return dp[0];
}
96. 不同的二叉搜索树(区间DP)
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
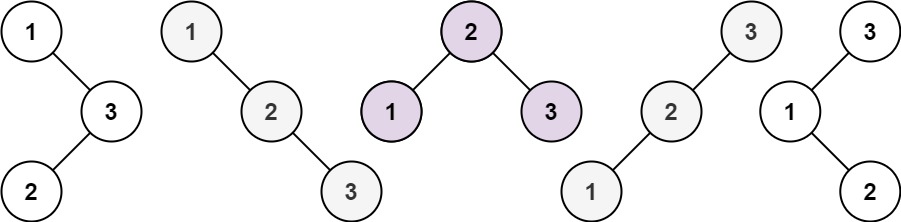
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1

//区间DP
class Solution {
public int numTrees(int n) {
int[][] dp = new int[n+10][n+10];
for(int i = 0; i <= n+1; i++){
for(int j = 0; j<= n+1; j++){
if(i >= j) dp[i][j] = 1;
}
}
//dp[l][r] += dp[l][i-1] * dp[i+1][r];
for(int length = 2; length <= n; length++){
for(int l = 1; l + length -1 <= n; l++){
int r = l + length - 1;
for(int i = l; i <= r; i++){
dp[l][r] += dp[l][i-1]*dp[i+1][r];
}
}
}
return dp[1][n];
}
}
优化:1n的二叉搜索种类树和2n+1是一样的,由于是连续的,因此只和数量有关
所以dp优化为1维:dp[i]代表i数量节点的二叉搜索树种类个数。
此时依旧可以采用区间dp的思想,k分割 dp[i] = dp[k-1]*dp[i-k];
k-1 ====> 前k-1的总数,
i-k======>后k~i的总数
代码:
class Solution {
public int numTrees(int n) {
int[] dp = new int[n+10];
dp[0] = 1;
for(int i = 1; i <= n; i++){
for(int k = 1; k <= i; k++){
dp[i] += dp[k-1] * dp[i-k];
}
}
return dp[n];
}
}
97. 交错字符串
给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串:
s = s1 + s2 + ... + snt = t1 + t2 + ... + tm|n - m| <= 1- 交错 是
s1 + t1 + s2 + t2 + s3 + t3 + ...或者t1 + s1 + t2 + s2 + t3 + s3 + ...
注意:a + b 意味着字符串 a 和 b 连接。
示例 1:
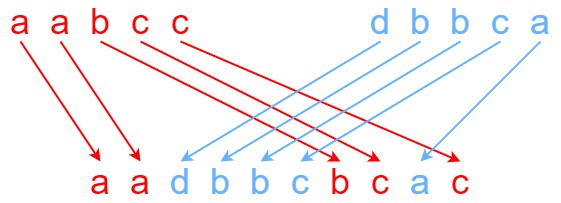
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出:true
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
char[] cs1 = s1.toCharArray(),cs2 = s2.toCharArray(),cs3 = s3.toCharArray();
int l1 = s1.length(),l2 = s2.length(),l3 = s3.length();
if(l1 + l2 != l3) return false;
boolean[][] dp = new boolean[l1+1][l2+1];
dp[0][0] = true;
for(int i = 0; i <= l1; i++){
for(int j = 0; j <= l2; j++){
if(i > 0){
dp[i][j] = dp[i-1][j] && cs1[i-1] == cs3[i + j - 1];
}
if(j > 0){
dp[i][j] |= dp[i][j-1] && cs2[j-1] == cs3[i + j - 1];
}
}
}
return dp[l1][l2];
}
}
//空间压缩
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
char[] cs1 = s1.toCharArray(),cs2 = s2.toCharArray(),cs3 = s3.toCharArray();
int l1 = s1.length(),l2 = s2.length(),l3 = s3.length();
if(l1 + l2 != l3) return false;
boolean[] dp = new boolean[l2+1];
dp[0] = true;
for(int i = 0; i <= l1; i++){
for(int j = 0; j <= l2; j++){
if(i > 0){
dp[j] = dp[j] && cs1[i-1] == cs3[i+j-1];
}
if(j > 0){
dp[j] |= dp[j-1] && cs2[j-1] == cs3[i+j-1];
}
}
}
return dp[l2];
}
}
120. 三角形最小路径和
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]]
输出:-10
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int[] dp = new int[n+1];
for(int i = n - 1; i >= 0; i--){
for(int j = 0; j <= i; j++){//从前向后,可以避免更新的元素,影响下一个更新判断
dp[j] = Math.min(dp[j],dp[j+1]) + triangle.get(i).get(j);
}
}
return dp[0];
}
}
121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
class Solution {
public int maxProfit(int[] prices) {
//一直更新最小花费和最大利润
int profit = 0,cost = prices[0];
for(int price: prices){
profit = Math.max(profit,price-cost);
cost = Math.min(cost,price);
}
return profit;
}
}
122. 买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。
class Solution {
public int maxProfit(int[] prices) {
int have = -prices[0],no = 0;
for(int i = 1; i < prices.length; i++){
no = Math.max(no,(have+prices[i]));
have = Math.max((no-prices[i]),have);
}
return no;
}
}
123. 买卖股票的最佳时机 III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4]
输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
class Solution {
public static int maxProfit(int[] prices) {
int n = prices.length;
int[][] dp = new int[2][3];
dp[0][1] = (int)-1e5+1;
dp[0][2] = (int)-1e5+1;
dp[1][0] = -prices[0];
dp[1][1] = (int)-1e5+1;
dp[1][2] = (int)-1e5+1;
for (int i = 1; i < n; i++) {
dp[0][1] = Math.max(dp[0][1], dp[1][0] + prices[i]);
dp[0][2] = Math.max( dp[0][2], dp[1][1] + prices[i] );
dp[1][0] = Math.max( dp[1][0], dp[0][0] - prices[i]);
dp[1][1] = Math.max( dp[1][1], dp[0][1] - prices[i]);
dp[1][2] = Math.max( dp[1][2], dp[0][2] - prices[i]);
}
return dp[0][2];
}
}
128. 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109
class Solution {
public int longestConsecutive(int[] nums) {
//使用map存储,(x,y)代表:包含x的序列,最大长度为y
HashMap<Integer,Integer> map = new HashMap<>();
int maxLength = 0;
for(int num: nums){
if(!map.containsKey(num)){
int left = map.getOrDefault(num-1,0);
int right = map.getOrDefault(num+1,0);
int curLen = left + right + 1;
maxLength = Math.max(maxLength,curLen);
map.put(num,-1);
//更新左右边界的最大长度
map.put(num-left,curLen);
map.put(num+right,curLen);
}
}
return maxLength;
}
}
区间DP
131. 分割回文串
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a"
输出:[["a"]]
class Solution {
public List<List<String>> partition(String s) {
List<List<String>> result = new ArrayList<>();
List<String> path = new ArrayList<>();
boolean[][] isPal = new boolean[s.length()][s.length()];
//获取isPal时,用到了区间DP
for(int length = 1; length <= s.length(); length++){
for(int start = 0; start+length <= s.length(); start++){
int end = start + length - 1;
if(length == 1) isPal[start][end] = true;
else if(length == 2){
isPal[start][end] = s.charAt(start) == s.charAt(end);
}else{
isPal[start][end] = s.charAt(start) == s.charAt(end) && isPal[start+1][end-1];
}
}
}
dfs(s,result,path,isPal,0);
return result;
}
public void dfs(String s, List<List<String>> result,List<String> path,boolean[][] isPal,int curIndex){
if(curIndex == s.length()){
result.add(new ArrayList<String>(path));
return;
}
for(int i = curIndex; i < s.length(); i++){
if(isPal[curIndex][i]){
path.add(s.substring(curIndex,i+1));
dfs(s,result,path,isPal,i+1);
path.remove(path.size()-1);
}
}
}
}
132. 分割回文串 II
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文。
返回符合要求的 最少分割次数 。
示例 1:
输入:s = "aab"
输出:1
解释:只需一次分割就可将 s 分割成 ["aa","b"] 这样两个回文子串。
示例 2:
输入:s = "a"
输出:0
示例 3:
输入:s = "ab"
输出:1
class Solution {
public int minCut(String s) {
int len = s.length();
if(len < 2) return 0;
boolean[][] isPal = new boolean[len][len];
//区间dp求 是否为回文串
for(int length = 1; length <= len; length++){
for(int start = 0; start+length <= len; start++){
int end = start + length - 1;
if(s.charAt(end) == s.charAt(start)){
if(end - start < 2 || isPal[start+1][end-1]){
isPal[start][end] = true;
}
}
}
}
//dp[i]代表切分到i位置时,最少需要的次数
int[] dp = new int[len];
//初始化,i个字符,最多切分i-1次
for(int i = 0; i < len; i++){
dp[i] = i;
}
for(int i = 1; i < len; i++){
if(isPal[0][i]){
dp[i] = 0;
}else{
for(int j = 0; j < i; j++){
if(isPal[j+1][i]){
//j和j+1之间为切分点,不断更新dp[i]
//dp[j]+1 代表:切分点之前的切割次数 + 本次切割
dp[i] = Math.min(dp[i],dp[j]+1);
}
}
}
}
return dp[len-1];
}
}
十、模拟
38. 外观数列
给定一个正整数 n ,输出外观数列的第 n 项。
「外观数列」是一个整数序列,从数字 1 开始,序列中的每一项都是对前一项的描述。
你可以将其视作是由递归公式定义的数字字符串序列:
countAndSay(1) = "1"countAndSay(n)是对countAndSay(n-1)的描述,然后转换成另一个数字字符串。
前五项如下:
1. 1
2. 11
3. 21
4. 1211
5. 111221
第一项是数字 1
描述前一项,这个数是 1 即 “ 一 个 1 ”,记作 "11"
描述前一项,这个数是 11 即 “ 二 个 1 ” ,记作 "21"
描述前一项,这个数是 21 即 “ 一 个 2 + 一 个 1 ” ,记作 "1211"
描述前一项,这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ,记作 "111221"
要 描述 一个数字字符串,首先要将字符串分割为 最小 数量的组,每个组都由连续的最多 相同字符 组成。然后对于每个组,先描述字符的数量,然后描述字符,形成一个描述组。要将描述转换为数字字符串,先将每组中的字符数量用数字替换,再将所有描述组连接起来。
例如,数字字符串 "3322251" 的描述如下图:

示例 1:
输入:n = 1
输出:"1"
解释:这是一个基本样例。
示例 2:
输入:n = 4
输出:"1211"
解释:
countAndSay(1) = "1"
countAndSay(2) = 读 "1" = 一 个 1 = "11"
countAndSay(3) = 读 "11" = 二 个 1 = "21"
countAndSay(4) = 读 "21" = 一 个 2 + 一 个 1 = "12" + "11" = "1211"
public static String countAndSay(int n) {
if (n == 1) return "1";
String number = "1";
StringBuilder stringBuilder = null;
for (int t = 1; t < n; t ++){
stringBuilder = new StringBuilder();
int count = 1;
for (int i = 1; i < number.length(); i++){
if (number.charAt(i-1) != number.charAt(i)){
stringBuilder.append(count);
count = 0;
stringBuilder.append(number.charAt(i-1));
}
count++;
}
stringBuilder.append(count);
stringBuilder.append(number.charAt(number.length()-1));
number = stringBuilder.toString();
}
return stringBuilder.toString();
}
48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
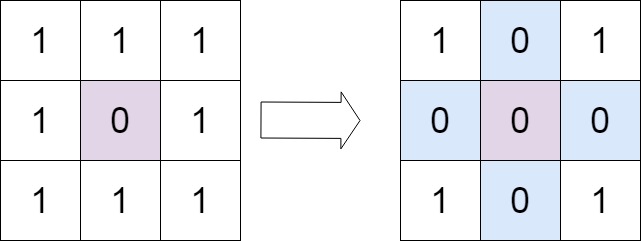
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
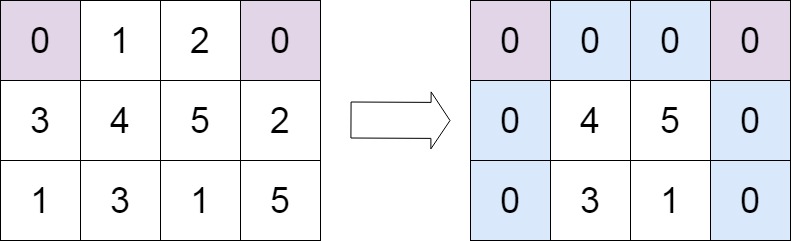
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
第x行数据旋转后变为倒数第x列
[row] [col] = [n-1-col] [row]
public void rotate(int[][] matrix) {
int l = matrix.length;
for (int i = 0; i < l/2; i++){
for (int j = 0; j < (l+1)/2; j++){
int temp = matrix[i][j];
matrix[i][j] = matrix[l-j-1][i];
matrix[l-j-1][i] = matrix[l-i-1][l-j-1];
matrix[l-i-1][l-j-1] = matrix[j][l-i-1];
matrix[j][l-i-1] = temp;
}
}
}
54. 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
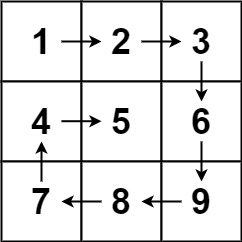
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
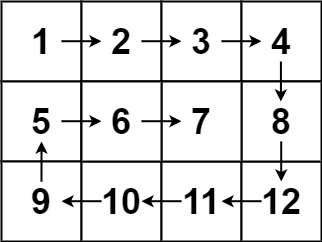
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
public static List<Integer> spiralOrder(int[][] matrix) {
int curRow = 0;
int curCol = 0;
List<Integer> list = new ArrayList<>();
while (inMatrix(curRow,curCol,matrix)){
while (inMatrix(curRow,curCol,matrix) ){
list.add(matrix[curRow][curCol]);
matrix[curRow][curCol++] = 101;
}
curCol--;
curRow++;
while (inMatrix(curRow,curCol,matrix) ){
list.add(matrix[curRow][curCol]);
matrix[curRow++][curCol] = 101;
}
curRow--;
curCol--;
while (inMatrix(curRow,curCol,matrix)){
list.add(matrix[curRow][curCol]);
matrix[curRow][curCol--] = 101;
}
curCol++;
curRow--;
while (inMatrix(curRow,curCol,matrix)){
list.add(matrix[curRow][curCol]);
matrix[curRow--][curCol] = 101;
}
curRow++;
curCol++;
}
return list;
}
public static boolean inMatrix(int row,int col,int[][] matrix){
return row < matrix.length && row >=0 &&
col < matrix[0].length && col >= 0 &&
matrix[row][col] != 101;
}
57. 插入区间
给你一个 无重叠的 ,按照区间起始端点排序的区间列表。
在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。
示例 1:
输入:intervals = [[1,3],[6,9]], newInterval = [2,5]
输出:[[1,5],[6,9]]
示例 2:
输入:intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出:[[1,2],[3,10],[12,16]]
解释:这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。
示例 3:
输入:intervals = [], newInterval = [5,7]
输出:[[5,7]]
示例 4:
输入:intervals = [[1,5]], newInterval = [2,3]
输出:[[1,5]]
示例 5:
输入:intervals = [[1,5]], newInterval = [2,7]
输出:[[1,7]]
public static int[][] insert(int[][] intervals, int[] newInterval) {
if (intervals.length == 0) return new int[][]{newInterval};
List<int[]> list = new ArrayList<>();
boolean flag = false;
for (int[] interval : intervals) {
int left = interval[0], right = interval[1];
if (newInterval[1] < left) {//newIntervals在左边
if (!flag) {
list.add(newInterval);
flag = true;
}
list.add(interval);
} else if (newInterval[0] > right) {//new在右边,右侧可能还会有和newInvals交叉的,所以先不加入newInterval
list.add(interval);
} else {//交叉,计算边界
newInterval[0] = Math.min(newInterval[0], left);
newInterval[1] = Math.max(newInterval[1], right);
}
}
if (!flag){
list.add(newInterval);
}
return list.toArray(new int[list.size()][]);
}
59. 螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
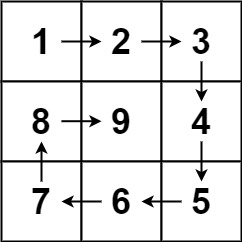
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
public int[][] generateMatrix(int n) {
int top = 0, bottom = n - 1, right = n - 1, left = 0, cur = 1;
int[][] matrix = new int[n][n];
while (cur <= n * n) {
for (int i = left; i <= right; i++) {//左 -》 右
matrix[top][i] = cur++;
}
top++;
for (int i = top; i <= bottom; i++) {// 上 -》 下
matrix[i][right] = cur++;
}
right--;
for (int i = right; i >= left; i--) {//右 -》左
matrix[bottom][i] = cur++;
}
bottom--;
for (int i = bottom; i>= top; i--){//下 -》 上
matrix[i][left] = cur++;
}
left++;
}
return matrix;
}
73. 矩阵置零
给定一个 *m* x *n* 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:

输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:

输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
解题方法
方法一:使用标记数组
我们可以用两个标记数组分别记录每一行和每一列是否有零出现。
具体地,我们首先遍历该数组一次,如果某个元素为 0,那么就将该元素所在的行和列所对应标记数组的位置置为 true。最后我们再次遍历该数组,用标记数组更新原数组即可。
方法二:
使我们可以用矩阵的第一行和第一列代替方法一中的两个标记数组,以达到 O(1) 的额外空间。但这样会导致原数组的第一行和第一列被修改,无法记录它们是否原本包含 0。因此我们需要额外使用两个标记变量分别记录第一行和第一列是否原本包含 0。
在实际代码中,我们首先预处理出两个标记变量,接着使用其他行与列去处理第一行与第一列,然后反过来使用第一行与第一列去更新其他行与列,最后使用两个标记变量更新第一行与第一列即可
public void setZeroes(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
boolean rowHasZero = false, colHasZero = false;
for (int[] ints : matrix) {
if (ints[0] == 0) {
colHasZero = true;
break;
}
}
for (int i = 0; i < n; i++) {
if (matrix[0][i] == 0) {
rowHasZero = true;
break;
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j] == 0) {
matrix[i][0] = matrix[0][j] = 0;
}
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][0] == 0 || matrix[0][j] == 0) {
matrix[i][j] = 0;
}
}
}
if (rowHasZero) {
for (int i = 0; i < n; i++) {
matrix[0][i] = 0;
}
}
if (colHasZero) {
for (int i = 0; i < m; i++) {
matrix[i][0] = 0;
}
}
}
92. 反转链表 II
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
示例 1:
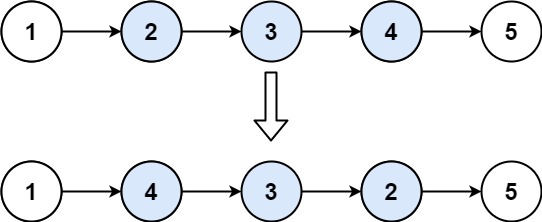
输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]
示例 2:
输入:head = [5], left = 1, right = 1
输出:[5]
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
// 使用头插法,不断向第一个需要反转的前面插入
ListNode dummyNode = new ListNode(-1);
dummyNode.next = head;
ListNode pre = dummyNode;
for(int i = 0; i < left-1; i++){
pre = pre.next;
}
ListNode cur = pre.next;
ListNode next = null;
for(int i = 0; i < right - left ;i++){
next = cur.next;
cur.next = next.next;
next.next = pre.next;
pre.next = next;
}
return dummyNode.next;
}
}
十一、排序
147. 对链表进行插入排序
给定单个链表的头 head ,使用 插入排序 对链表进行排序,并返回 排序后链表的头 。
插入排序 算法的步骤:
- 插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
- 每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
- 重复直到所有输入数据插入完为止。
下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时,从输入数据中删除一个元素(红色),并就地插入已排序的列表中。
对链表进行插入排序。

示例 1:
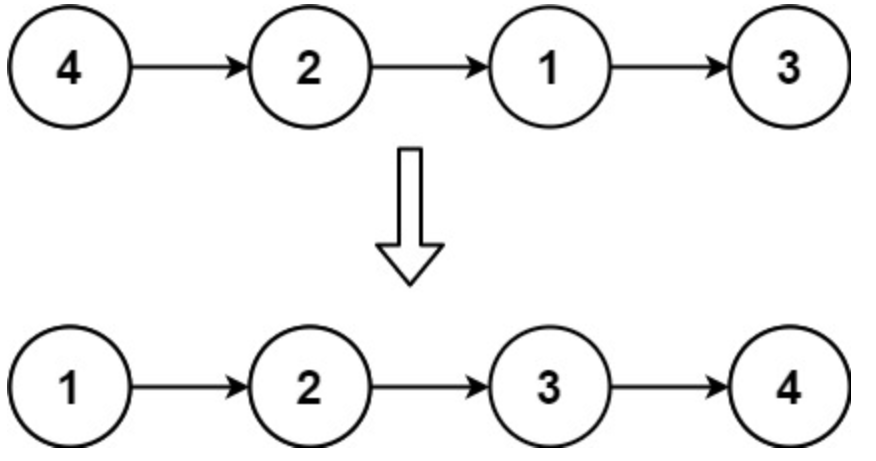
输入: head = [4,2,1,3]
输出: [1,2,3,4]
思路:

class Solution {
public ListNode insertionSortList(ListNode head) {
if(head == null) return head;
ListNode dummyHead = new ListNode(-1);
dummyHead.next = head;
ListNode lastSort = head, cur = head.next;
while(cur != null){
//如果当前node.val > 排好序的最后节点,排好序的节点++
if(cur.val >= lastSort.val){
lastSort = lastSort.next;
}else{//需要 插入排好序的最后节点的 前面
ListNode pre = dummyHead;
//从头找比cur.val大的,为pre.next
while(pre.next.val <= cur.val){
pre = pre.next;
}
//交换位置,交换后为:pre cur pre.next ...
lastSort.next = cur.next;
cur.next = pre.next;
pre.next = cur;
}
cur = lastSort.next; //提取if语句的cur移动
}
return dummyHead.next;
}
}
148. 排序链表
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
示例 1:
输入:head = [4,2,1,3]
输出:[1,2,3,4]
示例 2:
输入:head = [-1,5,3,4,0]
输出:[-1,0,3,4,5]
示例 3:
输入:head = []
输出:[]
思路:

class Solution {
public ListNode sortList(ListNode head) {
//出口
if(head == null || head.next == null) return head;
//找到链表中点
ListNode slow = head,fast = head;
while(fast.next != null && fast.next.next != null){
slow = slow.next;
fast = fast.next.next;
}
ListNode right = slow.next;
slow.next = null;
ListNode left = head;
//递归左右链表
left = sortList(left);
right = sortList(right);
//合并
ListNode dummyNode = new ListNode(-1);
ListNode cur = dummyNode;
while(left != null && right != null){
if(left.val < right.val){
cur.next = left;
left = left.next;
}else{
cur.next = right;
right = right.next;
}
cur = cur.next;
}
cur.next = left != null? left : right;
return dummyNode.next;
}
}
十二、贪心
11. 盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:

输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
public int maxArea(int[] height) {
//双指针指向首尾,只有移动短板,水池才有可能变大
int left = 0,right = height.length-1;
int maxSum = 0;
while (left < right){
maxSum = height[left] < height[right]?
Math.max(maxSum,height[left++]*(right -left)):
Math.max(maxSum,height[right--]*(right-left));
}
return maxSum;
}
134. 加油站
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
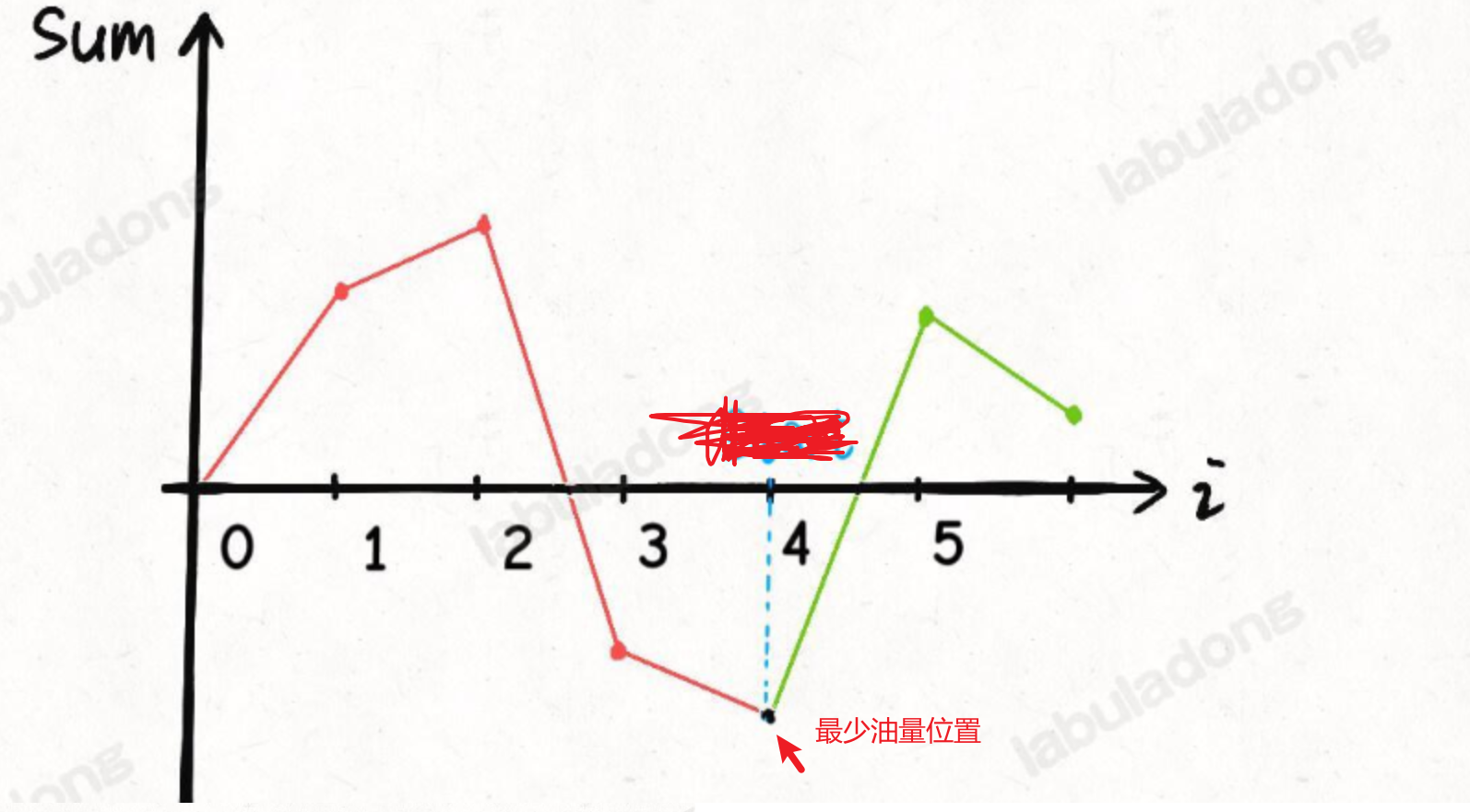 变为:
变为: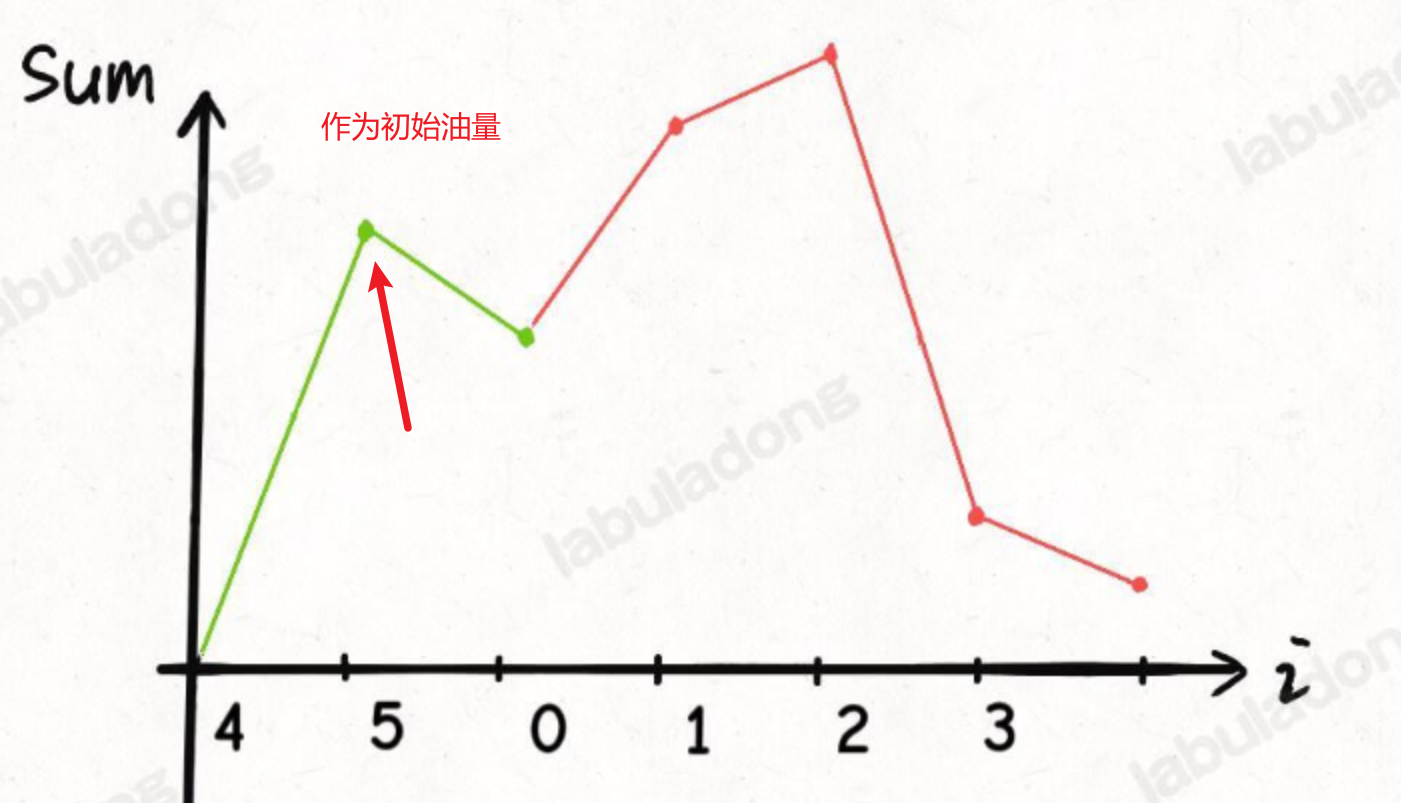
分析如上图:需要找到最小的且小于0的当前油量,以下一个位置为起点,作为初始油量
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
int sum = 0,min = 0,minIndex = -1;
for(int i = 0; i < gas.length; i++){
sum += (gas[i] - cost[i]);
if(sum < min){ //因为有唯一解,所以找最小的且小于0的当前油量
min = sum;
minIndex = i;
}
}
//找到后,以下一个位置为起点,就可以保证所有位置的油量都>0,求余是防止最后一个点是最小油量
return sum < 0 ?-1:(minIndex + 1) % gas.length;
}
}
135. 分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到
1个糖果。 - 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
示例 1:
输入:ratings = [1,0,2]
输出:5
解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
示例 2:
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
两次遍历:
- 从左向右,保证rate[i]>rata[i-1]时dp[i] > dp[i-1]
- 从右向左,保证rate[i]>rate[i+1]时dp[i]>dp[i+1]
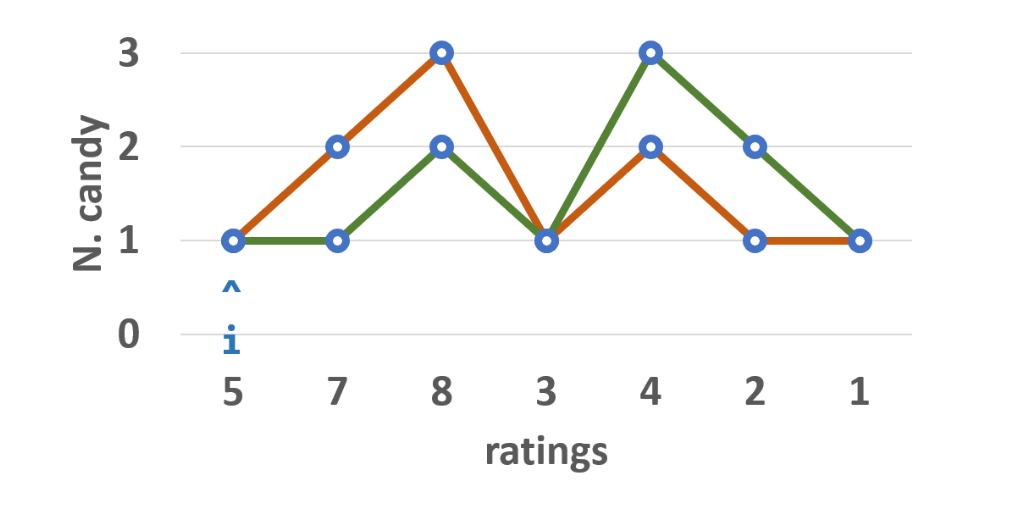
黄色:是从左向右遍历
绿色:是从右向左遍历
要同时满足这两个要求,要求取最大值
更改代码,替换为一个数组,第二次遍历时dp[i] <= dp[i+1]才改变,也就保证了取最大值。
class Solution {
public int candy(int[] ratings) {
int[] dp = new int[ratings.length];
dp[0] = 1;
//从左向右,保证rate[i]>rata[i-1]时dp[i] > dp[i-1]
for(int i = 1; i < ratings.length; i++){
if(ratings[i] > ratings[i-1]){
dp[i] = dp[i-1]+1;
}else{
dp[i] = 1;
}
}
/*从右向左,保证rate[i]>rate[i+1]时dp[i]>dp[i+1]
问:为什么不会破坏上一次从左向右的遍历?
因为从左向右的遍历是保证了dp[i-1] 和 dp[i]的规律性
这次是保证dp[i] 和 dp[i+1]的规律性
*/
int result = dp[ratings.length-1];
for(int i = ratings.length-2; i >= 0; i--){
if(ratings[i] > ratings[i+1] && dp[i] <= dp[i+1]){
dp[i] = dp[i+1]+1;
}
result += dp[i];
}
return result;
}
}
十三、滑动窗口
3. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串
public static int lengthOfLongestSubstring(String s) {
if (s.length() == 0) return 0;
//滑动窗口
int left = 0,right = 0,maxLength=-1;
//哈希表
HashMap<Character,Integer> hashMap = new HashMap<>();
for (;right < s.length();right++){
//不重复
if (hashMap.containsKey(s.charAt(right))){
//更新最大长度
maxLength = Math.max(maxLength,right-left);
//左边界走过的区域,不计算
left = Math.max(left,hashMap.get(s.charAt(right))+1);
}
//更新位置
hashMap.put(s.charAt(right),right);
}
return Math.max(maxLength,right-left);
}
十四、深度优先搜索
129. 求根节点到叶节点数字之和
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:
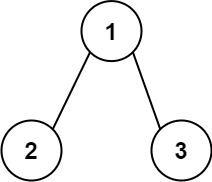
输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
示例 2:
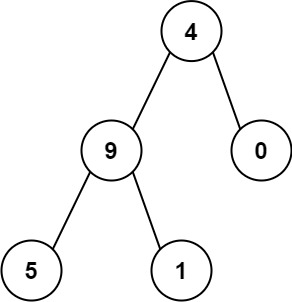
输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
class Solution {
public int sumNumbers(TreeNode root) {
return getSum(root,0);
}
public int getSum(TreeNode node,int cur){
if(node == null) return 0;
cur = cur * 10 + node.val;
if(node.left == null && node.right == null){
return cur;
}
return getSum(node.left,cur)+getSum(node.right,cur);
}
}
130. 被围绕的区域
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例 1:
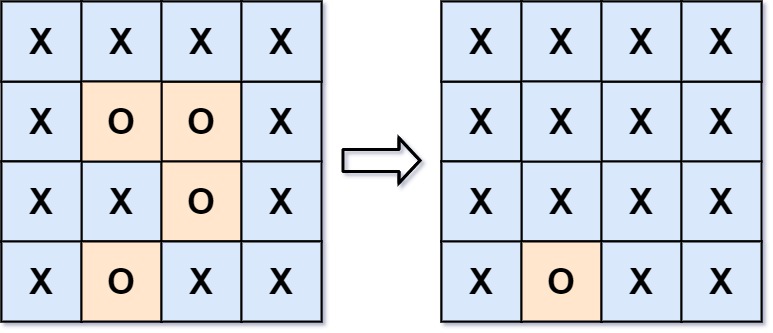
输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例 2:
输入:board = [["X"]]
输出:[["X"]]
class Solution {
public void solve(char[][] board) {
int m = board.length;
int n = board[0].length;
for(int i = 0; i < m; i++){
dfs(board,i,0);
dfs(board,i,n-1);
}
for(int j = -0; j < n; j++){
dfs(board,0,j);
dfs(board,m-1,j);
}
for(int i = 0; i < board.length; i++){
for(int j = 0; j < board[0].length; j++){
board[i][j] = board[i][j] == 'Q'?'O':'X';
}
}
}
public void dfs(char[][] board,int i,int j){
if(i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] != 'O') return;
board[i][j] = 'Q';
dfs(board,i-1,j);
dfs(board,i+1,j);
dfs(board,i,j-1);
dfs(board,i,j+1);
}
}
十五、单调栈
十六、Mirrors遍历
Morris遍历细节
假设来到当前节点cur,开始时cur来到头节点位置
1)如果cur没有左孩子,cur向右移动(cur = cur.right)
2)如果cur有左孩子,找到左子树上最右的节点mostRight:
a.如果mostRight的右指针指向空,让其指向cur, 然后cur向左移动(cur = cur.left)
b.如果mostRight的右指针指向cur,让其指向null, 然后cur向右移动(cur = cur.right)
cur为空时遍历停止
public static void morrisTravel(Node head){
if (head == null){
return;
}
Node cur = head;
Node mostRightNode;
while (cur != null){
mostRightNode = cur.left;
//cur有左孩子
if (mostRightNode != null){
//找到左子树的最右节点,并且保证mostRight不会移动回cur
while (mostRightNode.right != null && mostRightNode.right != cur){
mostRightNode = mostRightNode.right;
}
//看mostRight是否有right
if (mostRightNode.right == null){
//没有right,则添加right指向cur
mostRightNode.right = cur;
//并且cur向左遍历
cur = cur.left;
//继续这一循环
continue;
}
//指向了cur
else {
//断开连接
mostRightNode.right = null;
//cur向右移动
}
}
//cur没有左孩子,cur向右移动
cur = cur.right;
}
}
先序遍历
//先序:能回来两次的节点,第一次打印,第二次不打印
// 只能到一次的节点,直接打印
public static void morrisPreTravel(Node head){
if (head == null){
return;
}
Node cur = head;
Node mostRightNode;
while (cur != null){
mostRightNode = cur.left;
//cur有左孩子
//进入if:能回cur两次的
if (mostRightNode != null){
//找到左子树的最右节点,并且保证mostRight不会移动回cur
while (mostRightNode.right != null && mostRightNode.right != cur){
mostRightNode = mostRightNode.right;
}
//看mostRight是否有right
if (mostRightNode.right == null){
//第一次来到当前节点
System.out.print(cur.value+" ");
//没有right,则添加right指向cur
mostRightNode.right = cur;
//并且cur向左遍历
cur = cur.left;
//继续这一循环
continue;
}
//指向了cur
else {
//第二次来到cur
//不打印
//断开连接
mostRightNode.right = null;
//cur向右移动
}
}
//没有左子树的,走到else
else {
System.out.print(cur.value+" ");
}
//cur没有左孩子,cur向右移动
cur = cur.right;
}
}
中序
//中序:能回来两次的节点,第一次不打印,第二次打印
// 只能到一次的节点,直接打印
public static void morrisMediaTravel(Node head){
if (head == null){
return;
}
Node cur = head;
Node mostRightNode;
while (cur != null){
mostRightNode = cur.left;
//cur有左孩子
//进入if:能回cur两次的
if (mostRightNode != null){
//找到左子树的最右节点,并且保证mostRight不会移动回cur
while (mostRightNode.right != null && mostRightNode.right != cur){
mostRightNode = mostRightNode.right;
}
//看mostRight是否有right
if (mostRightNode.right == null){
//没有right,则添加right指向cur
mostRightNode.right = cur;
//并且cur向左遍历
cur = cur.left;
//继续这一循环
continue;
}
//指向了cur
else {
//第二次来到cur
//不打印
//断开连接
mostRightNode.right = null;
//cur向右移动
}
}
System.out.print(cur.value+" ");
//cur没有左孩子,cur向右移动
cur = cur.right;
}
}
是否为线索二叉树
可以根据中序遍历改编
//中序:能回来两次的节点,第一次不打印,第二次打印
// 只能到一次的节点,直接打印
public static boolean morrisMediaTravel(Node head){
if (head == null){
return true ;
}
Node cur = head;
Node mostRightNode;
int preNodeValue = Integer.MIN_VALUE;
while (cur != null){
mostRightNode = cur.left;
//cur有左孩子
//进入if:能回cur两次的
if (mostRightNode != null){
//找到左子树的最右节点,并且保证mostRight不会移动回cur
while (mostRightNode.right != null && mostRightNode.right != cur){
mostRightNode = mostRightNode.right;
}
//看mostRight是否有right
if (mostRightNode.right == null){
//没有right,则添加right指向cur
mostRightNode.right = cur;
//并且cur向左遍历
cur = cur.left;
//继续这一循环
continue;
}
//指向了cur
else {
//第二次来到cur
//不打印
//断开连接
mostRightNode.right = null;
//cur向右移动
}
}
//System.out.print(cur.value+" ");
if (cur.value < preNodeValue){
return false;
}
preNodeValue = cur.value;
//cur没有左孩子,cur向右移动
cur = cur.right;
}
return true;
}
94. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
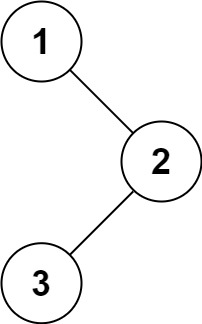
输入:root = [1,null,2,3]
输出:[1,3,2]
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
//Mirrors遍历
TreeNode cur = root;
TreeNode mostRight = null;
List<Integer> result = new ArrayList<>();
if (root == null) return result;
while(cur != null){
mostRight = cur.left;
if(mostRight != null){
while(mostRight.right != null && mostRight.right != cur){
mostRight = mostRight.right;
}
if(mostRight.right == null){
mostRight.right = cur;
cur = cur.left;
continue;
}else{
mostRight.right = null;
}
}
result.add(cur.val);
cur = cur.right;
}
return result;
}
}
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
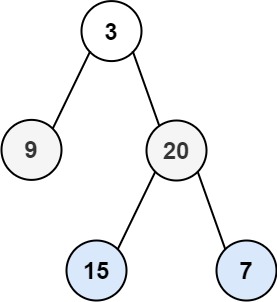
输入:root = [2,1,3]
输出:true
class Solution {
public boolean isValidBST(TreeNode root) {
TreeNode cur = root;
TreeNode mostRight = null,pre = null;
while(cur != null){
mostRight = cur.left;
if (mostRight != null){
while(mostRight.right != null && mostRight.right != cur){
mostRight = mostRight.right;
}
if(mostRight.right == null){
mostRight.right = cur;
cur = cur.left;
continue;
}else{
mostRight.right = null;
}
}
if(pre != null && cur.val <= pre.val){
return false;
}
pre = cur;
cur = cur.right;
}
return true;
}
}
99. 恢复二叉搜索树
给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。
示例 1:
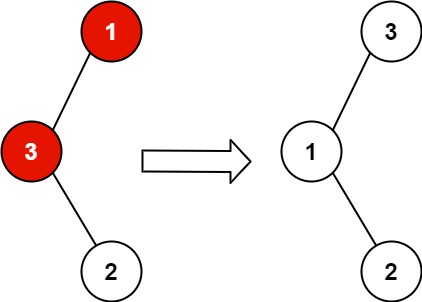
输入:root = [1,3,null,null,2]
输出:[3,1,null,null,2]
解释:3 不能是 1 的左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2:
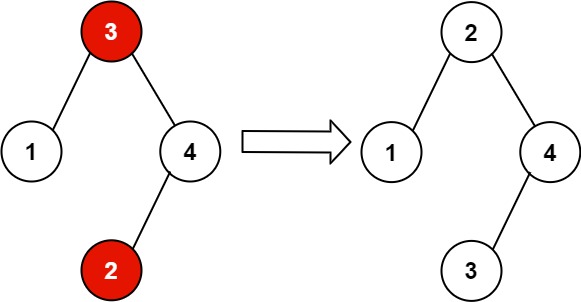
输入:root = [3,1,4,null,null,2]
输出:[2,1,4,null,null,3]
解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效
class Solution {
public void recoverTree(TreeNode root) {
TreeNode cur = root,mostRight = null,pre = null,x = null,y = null;
while(cur != null){
mostRight = cur.left;
if(mostRight != null){
while(mostRight.right != null && mostRight.right != cur){
mostRight = mostRight.right;
}
if(mostRight.right == null){
mostRight.right = cur;
cur = cur.left;
continue;
}else{
mostRight.right = null;
}
}
//如果错误的节点中序遍历时连续,会进入一次该if块,如果不连续,则进入两次
if(pre != null && cur.val <= pre.val){
//如果能进入两次,那么第一次的cur不需要交换,第二次的才需要
x = cur;
//如果能进入两次,那么第一次的pre是错误的位置,需要交换,第二次不需要
if(y == null){
y = pre;
}
}
pre = cur;
cur = cur.right;
}
int temp = x.val;
x.val = y.val;
y.val = temp;
}
}
114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:

输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [0]
输出:[0]
/*- morris :
若当前节点的左节点存在,则将本节点放在放到左节点的最右边,再访问左节点;(省略了第二次到自己的一步) 若左节点不存在,则直接访问 右节点
- 本题 :
若当前节点的左节点存在,则将右节点放到左节点的最右边,再将左节点放到右节点处,访问右节点; 若左节点不存在,则直接访问右节点*/
class Solution {
public void flatten(TreeNode root) {
if(root == null) return;
TreeNode cur = root,mostRight = null;
while(cur != null){
mostRight = cur.left;
if(mostRight != null){
while(mostRight.right != null && mostRight.right != cur){
mostRight = mostRight.right;
}
mostRight.right = cur.right;
cur.right = cur.left;
cur.left = null;
}
cur = cur.right;
}
}
}
十七、脑筋急转弯
521. 最长特殊序列 Ⅰ
给你两个字符串 a 和 b,请返回 这两个字符串中 最长的特殊序列 的长度。如果不存在,则返回 -1 。
「最长特殊序列」 定义如下:该序列为 某字符串独有的最长子序列(即不能是其他字符串的子序列) 。
字符串 s 的子序列是在从 s 中删除任意数量的字符后可以获得的字符串。
- 例如,
"abc"是"aebdc"的子序列,因为删除"a***e***b***d\***c"中斜体加粗的字符可以得到"abc"。"aebdc"的子序列还包括"aebdc"、"aeb"和""(空字符串)。
示例 1:
输入: a = "aba", b = "cdc"
输出: 3
解释: 最长特殊序列可为 "aba" (或 "cdc"),两者均为自身的子序列且不是对方的子序列。
示例 2:
输入:a = "aaa", b = "bbb"
输出:3
解释: 最长特殊序列是 "aaa" 和 "bbb" 。
示例 3:
输入:a = "aaa", b = "aaa"
输出:-1
解释: 字符串 a 的每个子序列也是字符串 b 的每个子序列。同样,字符串 b 的每个子序列也是字符串 a 的子序列。
ublic int findLUSlength(String a, String b) {
return !a.equals(b)?Math.max(a.length(),b.length()):-1;
}
十八、Manacher
Manacher算法
/**
* @Author: 郜宇博
*/
public class Manacher {
public static void main(String[] args) {
String str1 = "abc1234321ab";
System.out.println(maxLcpsLength(str1));
}
/**
* 最长回文子串
* 变量:c:导致R右扩的中心点,R:回文右边界 i:当前点, i':i关于c的对称点
* p[]:可以忽略判断的点个数
* 分为两种大情况
* 1.i在R外,那么就正常向两边扩(不确定回文数)
* 2.i在R内,有分为三种情况
* 2.1。 当i'的回文区域在[L,R]内,可以忽略的点个数为i'的回文半径(已经确定该点回文数)
* 2.2。 当i'的回文区域在[L,R]外,也就是超过了L,可以忽略的点个数为R-i(已经确定该点回文数)
* 2.3. 当i'的回文区域在[L,R]上,也就是压线,可以忽略的点个数为R-i(不确定回文数,需要判断下一个位置)
* 当走完数组后,数组内最大值就是最大的回文半径
* 因为加入了特殊字符如:#1#2#2#1#
* 所以回文长度为 半径-1
*
*/
public static int maxLcpsLength(String str){
if (str == null || str.length() == 0) {
return 0;
}
//添加特殊符号后的数组
char[] charArr = manacherString(str);
//半径长度(包括自己)
int[] pArr = new int[charArr.length];
int max = Integer.MIN_VALUE;
//导致右边界的中心点
int center = -1;
//右边界
int right = -1;
for (int i = 0; i < charArr.length; i++) {
//半径长度, 也就是获取可以忽略的点数+1
pArr[i] = right > i ? Math.min(pArr[2*center-i],right-i):1;
//虽然有的情况已经确定了回文数,但是为了减少代码量,因此统一一个扩张接口。
while (i + pArr[i] <charArr.length && i-pArr[i] >= 0){
//判断两边是否相等
if (charArr[i + pArr[i] ] == charArr[i-pArr[i] ]){
pArr[i]++;
}
else {
break;
}
}
//扩张后,查看是否超过了R,超过则更新,并保存c
if (i + pArr[i] > right){
right = i + pArr[i];
center = i;
}
//更新max值
max = Math.max(max,pArr[i]);
}
System.out.println(Arrays.toString(pArr));
return max-1;
}
private static char[] manacherString(String str) {
char[] charArr = str.toCharArray();
char[] res = new char[str.length() * 2 + 1];
int index = 0;
for (int i = 0; i != res.length; i++) {
res[i] = (i & 1) == 0 ? '#' : charArr[index++];
}
return res;
}
}
题
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
class Solution {
public static String longestPalindrome(String s) {
char[] charArr = manacherString(s);
int Right = -1,Centre = -1,maxLength = -1,rc = 0,end,start;
int[] RLength = new int[charArr.length];
for (int i = 0; i < charArr.length; i++) {
RLength[i] = Right > i?Math.min(Right-i,RLength[2 * Centre - i]):1;
while (i + RLength[i] < charArr.length && i - RLength[i] >= 0){
if (charArr[i + RLength[i]] == charArr[i - RLength[i]]){
RLength[i]++;
}else {
break;
}
}
if (i + RLength[i] > Right){
Right = i + RLength[i];
Centre = i;
}
if (RLength[i] > maxLength){
rc = i;
maxLength = RLength[i];
}
}
StringBuilder stringBuilder = new StringBuilder();
start = rc /2 - ((maxLength-1)/2);
end = ((maxLength - 1)& 1) == 0? rc/2 + ((maxLength-1)/2):rc/2 + ((maxLength-1)/2)+1;
for (int i = start; i < end; i++){
stringBuilder.append(s.charAt(i));
}
return stringBuilder.toString();
}
public static char[] manacherString(String s) {
char[] charArr = new char[(s.length() << 1) + 1];
char[] sArr = s.toCharArray();
int index = 0;
for (int i = 0; i < charArr.length; i++){
charArr[i] = (i & 1) == 0?'#':sArr[index++];
}
return charArr;
}
}
十九、回溯
39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
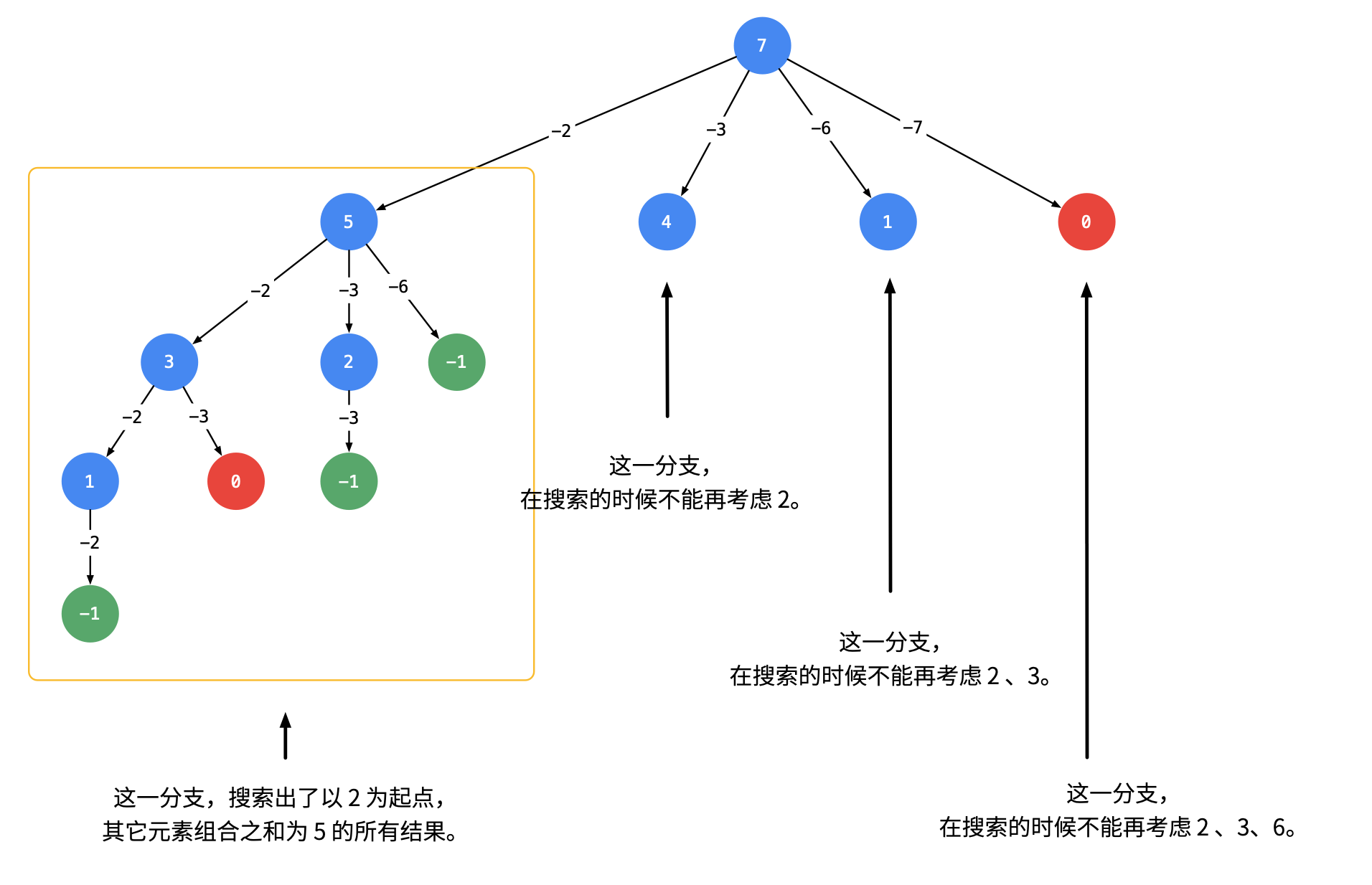
剪枝提速
根据上面画树形图的经验,如果 target 减去一个数得到负数,那么减去一个更大的树依然是负数,同样搜索不到结果。基于这个想法,我们可以对输入数组进行排序,添加相关逻辑达到进一步剪枝的目的;
排序是为了提高搜索速度,对于解决这个问题来说非必要。但是搜索问题一般复杂度较高,能剪枝就尽量剪枝。实际工作中如果遇到两种方案拿捏不准的情况,都试一下。
public static List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> result = new ArrayList<>();
Deque<Integer> path = new ArrayDeque<>();
Arrays.sort(candidates);
partition(result, candidates, 0, target, path);
return result;
}
public static void partition(List<List<Integer>> result,int[] candidates,int curIndex,int less,Deque<Integer> path){
if (less < 0) return;
if (less == 0) {
result.add(new ArrayList<>(path));
return;
}
for (int i = curIndex; i < candidates.length; i++){
//剪枝操作
if (candidates[i] > less) break;
//加入元素
path.addLast(candidates[i]);
partition(result,candidates,i,less-candidates[i],path);
//重置状态
path.removeLast();
}
}
40. 组合总和 II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
List<List<Integer>> result = new ArrayList<>();
Arrays.sort(candidates);
dfs(result,target,0,candidates,new ArrayList<>());
return result;
}
public void dfs(List<List<Integer>> result,int less,int curIndex,int[] candidates,List<Integer> part){
if (less < 0 ) return;
if (less == 0){
result.add(new ArrayList<>(part));
return;
}
for (int i = curIndex;i < candidates.length; i++){
if(less < candidates[i]) break; // 后面大的数字就不用算了
//如果上一个要加入的数字和当前数字一样(1,1,6)这个子结果不会跳过,是因为1 和 1 不是同一层的,
//candidates[i-1] == candidates[i]肯定在同一个位置(前面的排序确定了相同元素挨着)
if(i > curIndex && candidates[i-1] == candidates[i]) continue;
part.add(candidates[i]);
dfs(result,less-candidates[i],i+1,candidates,part);
part.remove(part.size()-1);
}
}
46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
public static List<List<Integer>> permute(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
//是否使用过
boolean[] isUse = new boolean[nums.length];
dfs(result,path,0,nums,isUse);
return result;
}
public static void dfs(List<List<Integer>> result,List<Integer> path,Integer curIndex,int[] nums,boolean[] isUse){
if (curIndex == nums.length){
result.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++){
if (!isUse[i]){
path.add(nums[i]);
isUse[i] = true;
dfs(result,path,curIndex+1,nums,isUse);
//使用完毕
isUse[i] = false;
path.remove(path.size()-1);
}
}
}
47. 全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
boolean[] isUse = new boolean[nums.length];
Arrays.sort(nums);
dfs(result,path,isUse,nums,0);
return result;
}
public void dfs(List<List<Integer>> result, List<Integer> path,boolean[] isUse,int[] nums, int curIndex){
if(curIndex == nums.length){
result.add(new ArrayList<>(path));
return;
}
for(int i = 0;i < nums.length; i++){
if(!isUse[i]){
//同一层的兄弟节点同一位置元素不能相同,并且保证这个元素确实被加入过,那么这次就不加入了
if(i > 0 && nums[i-1] == nums[i] && !isUse[i-1]) continue;
path.add(nums[i]);
isUse[i] = true;
dfs(result,path,isUse,nums,curIndex+1);
path.remove(path.size()-1);
isUse[i] = false;
}
}
}
}
77. 组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
class Solution {
public List<List<Integer>> combine(int n, int k) {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
dfs(result,path,1,n,k);
return result;
}
private void dfs(List<List<Integer>> result, List<Integer> path, int cur, int n, int k) {
if (path.size() == k){
result.add(new ArrayList<>(path));
return;
}
//剪枝:当前要加入的数值 + 接下来能加入的元素个数 - 1 = n
// i + k - path.size() - 1 <= n
for (int i = cur; i <= n - (k - path.size()) + 1; i++){
path.add(i);
dfs(result,path,i+1,n,k);
path.remove(path.size()-1);
}
}
}
78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
class Solution {
public static List<List<Integer>> subsets(int[] nums) {
List<Integer> path = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
result.add(new ArrayList<>());
for (int i = 1; i <= nums.length; i++){
dfs(result,path,i,nums,0);
}
return result;
}
private static void dfs(List<List<Integer>> result, List<Integer> path, int currentMax, int[] nums, int currentIndex) {
if (path.size() == currentMax){
result.add(new ArrayList<>(path));
return;
}
for (int i = currentIndex; i < nums.length;i ++){
path.add(nums[i]);
dfs(result,path,currentMax,nums,i+1);
path.remove(path.size()-1);
}
}
}
79. 单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
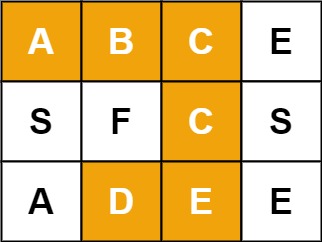
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
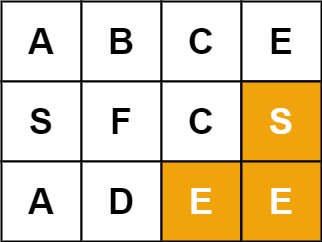
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出:true
示例 3:

解题思路:
本问题是典型的回溯问题,需要使用深度优先搜索(DFS)+ 剪枝解决。
深度优先搜索: 即暴力法遍历矩阵中所有字符串可能性。DFS 通过递归,先朝一个方向搜到底,再回溯至上个节点,沿另一个方向搜索,以此类推。
剪枝: 在搜索中,遇到“这条路不可能和目标字符串匹配成功”的情况,例如当前矩阵元素和目标字符不匹配、或此元素已被访问,则应立即返回,从而避免不必要的搜索分支。
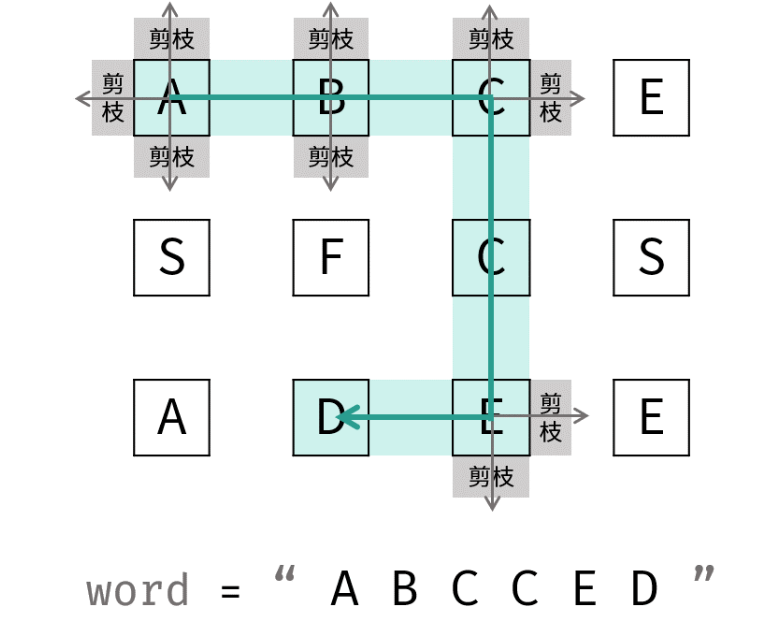
算法解析:
递归参数: 当前元素在矩阵 board 中的行列索引 i 和 j ,当前目标字符在 word 中的索引 k 。
终止条件:
- 返回 false : (1) 行或列索引越界 或 (2) 当前矩阵元素与目标字符不同或 (3) 当前矩阵元素已访问过 ( (3) 可合并至 (2) ) 。
- 返回 true : strIndex = len(word) - 1 ,即字符串 word 已全部匹配。
过程:
- 标记当前矩阵元素: 将
board[i][j]修改为 空字符 '' ,代表此元素已访问过,防止之后搜索时重复访问。 - 搜索下一单元格: 朝当前元素的 上、下、左、右 四个方向开启下层递归,使用 或 连接 (代表只需找到一条可行路径就直接返回,不再做后续 DFS ),并记录结果至 res 。
- 还原当前矩阵元素: 将
board[i][j]元素还原至初始值,即word[k]。
返回值: 返回布尔量 res ,代表是否搜索到目标字符串。
使用空字符做标记是为了防止标记字符与矩阵原有字符重复。当存在重复时,此算法会将矩阵原有字符认作标记字符,从而出现错误。
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出:false
class Solution {
public boolean exist(char[][] board, String word) {
for (int i = 0; i < board.length; i++){
for (int j = 0; j < board[0].length; j++){
if (dfs(board,i,j,word.toCharArray(),0)){
return true;
}
}
}
return false;
}
private boolean dfs(char[][] board, int i, int j, char[] word, int strIndex) {
if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] != word[strIndex]) return false;
if (strIndex == word.length-1) return true;
board[i][j] = '\0';
boolean flag = dfs(board,i+1,j,word,strIndex+1) || dfs(board,i-1,j,word,strIndex+1) ||
dfs(board,i,j+1,word,strIndex+1)||dfs(board,i,j-1,word,strIndex+1);
board[i][j] = word[strIndex];
return flag;
}
}
90. 子集 II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
class Solution {
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<Integer> path = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
Arrays.sort(nums);
dfs(result,path,nums,0);
return result;
}
public void dfs(List<List<Integer>> result, List<Integer> path,int[] nums,int cur){
result.add(new ArrayList(path));
for(int i = cur; i < nums.length; i++){
if(i != cur && nums[i] == nums[i-1]) {
continue;
}
path.add(nums[i]);
dfs(result,path,nums,i+1);
path.remove(path.size()-1);
}
}
}
113. 路径总和 II
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
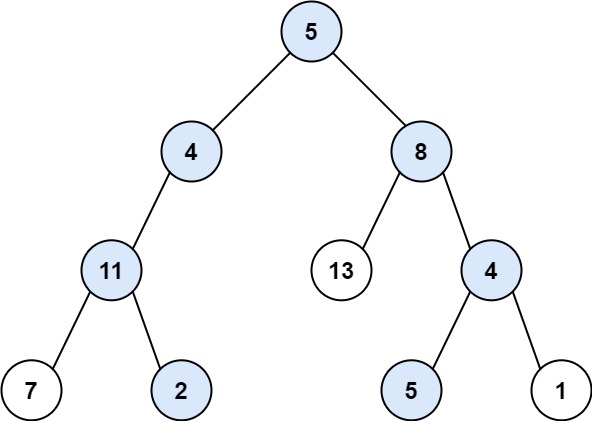
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
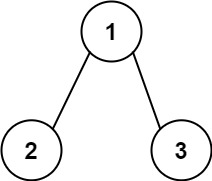
输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> result = new ArrayList<>();
if(root == null) return result;
List<Integer> path = new ArrayList<>();
dfs(result,path,root,targetSum);
return result;
}
public void dfs( List<List<Integer>> result,List<Integer> path,TreeNode node, int less){
if(node.left == null && node.right == null){
if(less == node.val) {
path.add(node.val);
result.add(new ArrayList<>(path));
path.remove(path.size()-1);
}
}
if(node.left != null){
path.add(node.val);
dfs(result,path,node.left,less-node.val);
path.remove(path.size()-1);
}
if(node.right != null){
path.add(node.val);
dfs(result,path,node.right,less-node.val);
path.remove(path.size()-1);
}
}
}
二十、二叉搜索树
95. 不同的二叉搜索树 II
给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。
示例 1:

输入:n = 3
输出:[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
示例 2:
输入:n = 1
输出:[[1]]
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<TreeNode> generateTrees(int n) {
List<TreeNode> result = new ArrayList<>();
if(n == 1) {
result.add(new TreeNode(1));
return result;
}
return process(1,n);
}
public List<TreeNode> process(int start,int end){
List<TreeNode> nodes = new ArrayList<>();
if(end <start){
nodes.add(null);
}else{
for(int i = start; i <= end; i++){
List<TreeNode> leftList = process(start, i-1);
List<TreeNode> rightList = process(i+1,end);
for(TreeNode left: leftList){
for(TreeNode right : rightList){
TreeNode node = new TreeNode(i);
node.left = left;
node.right = right;
nodes.add(node);
}
}
}
}
return nodes;
}
}
二十二、广度优先搜索
103. 二叉树的锯齿形层序遍历
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:[[3],[20,9],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
思路:使用LinkedList<TreeNode>作为路径存储,根据result.size()判断奇偶,来决定头插还是尾插路径
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
LinkedList<TreeNode> queue = new LinkedList<>();
if(root != null) queue.add(root);
while(!queue.isEmpty()){
int size = queue.size();
LinkedList<Integer> list = new LinkedList<>();
while( size-- > 0){
TreeNode pop = queue.pop();
if((result.size() & 1) == 1){
list.addFirst(pop.val);
}else{
list.addLast(pop.val);
}
if(pop.left != null) queue.add(pop.left);
if(pop.right != null) queue.add(pop.right);
}
result.add(list);
}
return result;
}
}
107. 二叉树的层序遍历 II
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:[[15,7],[9,20],[3]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
LinkedList<List<Integer>> result = new LinkedList<>();
LinkedList<TreeNode> queue = new LinkedList<>();
if(root != null) queue.add(root);
while(!queue.isEmpty()){
int size = queue.size();
List<Integer> list = new ArrayList<>();
while(size-- > 0){
TreeNode pop = queue.pop();
list.add(pop.val);
if(pop.left != null) queue.add(pop.left);
if(pop.right != null) queue.add(pop.right);
}
result.addFirst(list);
}
return result;
}
}
116. 填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:
输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
示例 2:
输入:root = []
输出:[]
class Solution {
public Node connect(Node root) {
if(root == null) return null;
LinkedList<Node> queue = new LinkedList<>();
queue.add(root);
Node pre = null;
while(!queue.isEmpty()){
int size = queue.size();
for(int i = 0; i < size; i++){
Node pop = queue.pop();
if(i != 0) pre.next = pop;
pre = pop;
if(pop.left != null) queue.add(pop.left);
if(pop.right != null) queue.add(pop.right);
}
}
return root;
}
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通