国科大卜东波算法设计作业

Question Number 1

You are interested in analyzing some hard-to-obtain data from two separate databases. Each database contains n numerical values, so there are 2n values total and you may assume that no two values are the same. You’d like to determine the median of this set of 2n values, which we will define here to be the nth smallest value. However, the only way you can access these values is through queries to the databases. In a single query, you can specify a value k to one of the two databases, and the chosen database will return the kth smallest value that it contains. Since queries are expensive, you would like to compute the median using as few queries as possible.

Give an algorithm that finds the median value using at most O(log n) queries.

思路

这个算法的思路是使用二分查找的思想来在两个数据库 D 和 D2 中查找合并后的第 n 小的值，也就是中位数。

1. 首先，初始化两个索引 p1 和 p2 分别指向两个数据库的中间位置，即 n / 2 处。

2. 然后，通过一个循环，进行了从 2 到 log2(n) 的迭代。这个循环的目的是不断地缩小待查找范围，直到找到中位数或者循环结束。

3. 在每次迭代中，首先查询两个数据库中索引位置 p1 和p2 处的值，分别为m1 和 m2。

4. 接下来，检查 m1 和 m2 是否相等。如果它们相等，那么这个值就是中位数，直接返回。

5. 如果 m1大于 m2，说明中位数一定在 m1 的左侧或 m2 的右侧，因此需要将索引 p1 向左移动，同时将索引 p2 向右移动，以缩小待查找范围。

   移动大小：

   \[p1 = p1 - n / (2^i)\\ p2 = p2 + n / (2^i) \]

6. 如果 m1 小于 m2，说明中位数一定在 m1 的右侧或 m2 的左侧，因此需要将索引 p1 向右移动，同时将索引 p2 向左移动，以缩小待查找范围。

   移动大小：

   \[p1 = p1 + n / (2^i)\\ p2 = p2 - n / (2^i) \]

7. 重复上述步骤直到找到中位数或者循环结束。

8. 最后，返回 m1 和 m2 中的较小值，作为合并后的第 n 小的值，也就是中位数。

这个算法的核心思想是不断地二分查找，并根据当前的中位数候选值来决定下一步查找的方向，以有效地找到中位数

时间复杂度分析

1. 初始化 p1 和 p2 需要 O(1) 时间。
2. 循环迭代从 2 到 log2(n) 次，其中 n 表示数据库中的元素总数。每次迭代都会执行以下操作：
   • 执行两次查询操作，即 Query(D1, p1) 和 Query(D2, p2)，这需要 O(1) 时间。
   • 进行条件判断和更新操作，这也需要 O(1) 时间。
3. 最终返回 min(m1, m2)，需要 O(1) 时间。

由于每次将问题的规模减少1/2，因此有：

\[T(n) = T(n/2) + c \]

因此复杂度为：

\[O(log_2n) \]

伪代码

Algorithm FindMedian(D1, D2, n):
	Input: 数据库D1{x1,x2,...xn},数据库D2{x1,x2,...xn}
    Output: 两个数据库中第n小的数值

    p1 = n / 2
    p2 = n / 2

    For i from 2 to log2(n) do
        m1 = Query(D1, p1)  //查询D1中第p1小的数
        m2 = Query(D2, p2)	//查询D2中第p2小的数

        If m1 == m2 then
            Return m1  
        EndIf

        If m1 > m2 then
            p1 = p1 - n / (2^i)
            p2 = p2 + n / (2^i)
        Else
            p1 = p1 + n / (2^i)
            p2 = p2 - n / (2^i)
        EndIf
    EndFor
    Return min(m1, m2)
END Algorithm

证明正确性

基本情况：n = 1时：p1 和 p2 都被初始化为整数 0和，而在循环之前，m1 和 m2 分别查询 D1 和 D2 中第 0 小的数。由于没有明确规定，可以假设查询到的值都是唯一的，因此 m1 和 m2 将分别等于 D1 和 D2 中的唯一值。由于 m1 和 m2 相等，算法将直接返回其中一个值，这是正确的。

归纳假设： n > 1 的情况。在这种情况下，算法使用二分法逐步缩小查询范围，直到找到中位数。

• 在循环的每一次迭代中，算法首先查询 D1 和 D2 中的第 p1 和 p2 小的数，分别为 m1 和 m2。
• 如果 m1 等于 m2，则算法直接返回其中一个值，因为这个值就是中位数。
• 如果 m1 大于 m2，则说明中位数在左侧。算法会将查询范围调整为左半部分，即 p1 和 p2 向左移动。
• 如果 m1 小于 m2，则说明中位数在右侧。算法会将查询范围调整为右半部分，即 p1 和 p2 向右移动。

算法在每次迭代中都缩小了查询范围，直到找到中位数或者 n 等于 2 时，返回两个候选中位数中的较小值。

综上所述，算法 FindMedian(D1, D2, n) 能够正确找到中位数，并且对于任何 n 的值都有效，即使 p1 和 p2 都为整数。

Question Number 2

Given any 10 points, p1, p2, ..., p10, on a two-dimensional Euclidean plane, please write an algorithm to find the distance between the closest pair of points.

(a) Using a brute-force algorithm to solve this problem, analyze the time complexity of your implemented brute-force algorithm and explain why the algorithm’s time complexity is O(n^2 ), where n is the number of points.

(b) Propose an improved algorithm to solve this problem with a time complexity better than the brute-force algorithm. Describe the algorithm’s idea and analyze its time complexity.

(a) Brute-Force

思路

暴力搜索的思路是对每一对点计算距离，并找到最小距离的一对点。该算法的时间复杂度分析如下：

1. 对于10个点，有10个点中的第一个点与其他9个点的距离需要计算。
2. 然后，有9个点中的第二个点与其他8个点的距离需要计算。
3. 以此类推，依次计算所有可能的点对的距离。

时间复杂度

总共需要计算的距离对数是 9 + 8 + 7 + ... + 1 = (10 * 9) / 2 = 45 对。即对于n个点，需要计算的距离对数为：

\[n(n-1)/2 \]

所以，该算法的时间复杂度为：

\[O(n^2) \]

其中n是点的数量。这是因为算法必须对每一对点都进行距离计算，导致时间复杂度与点的数量的平方成正比。

伪代码

Algorithm BruteForceClosestPair(points)
    Input: 一个点集 points，包含 n 个点
    Output: 最近的点对 closestPair 和它们之间的距离 minDistance

    minDistance = 无穷大
    closestPair = 无
    For i = 1 to n-1 do
        For j = i+1 to n do
            distance = 计算欧几里得距离(points[i], points[j])
            If distance < minDistance then
                minDistance = distance
                closestPair = (points[i], points[j])
            EndIf
        EndFor
    EndFor

    Return closestPair, minDistance
End Algorithm

证明正确性

要证明 BruteForceClosestPair(points) 算法的正确性，可以使用数学归纳法。

基本情况：，当点集中只有两个点时，算法将直接计算它们之间的距离，并返回这对点及其距离作为最近点对。这是显然正确的，因为只有两个点可以构成最近点对。

归纳假设：接下来，假设对于任意点集大小为 k 的情况，BruteForceClosestPair(points) 算法都能正确找到最近点对和它们之间的距离。

现在考虑点集大小为 k+1 的情况。算法首先初始化 minDistance 为无穷大，并将 closestPair 设为无。然后，算法使用两层嵌套循环遍历所有可能的点对，并计算它们之间的距离。如果找到一个距离小于 minDistance 的点对，算法将更新 minDistance 和 closestPair。

在完成循环后，算法返回 closestPair 和 minDistance。这确保了算法总是会找到最近的点对和它们之间的距离。

由于在基本情况下和归纳步骤中都假设算法是正确的，所以可以得出结论，BruteForceClosestPair(points) 算法对于任意点集都能正确找到最近点对和它们之间的距离。因此，该算法是正确的。

(b) Improved algorithm

思路

当点集的规模较小（n <= 3）时，使用暴力搜索是因为对于小规模的点集，暴力搜索的时间复杂度相对较低，且实现简单。对于包含很少点的情况，直接计算每一对点的距离并找到最小距离点对是一种高效的方法，因为计算的点对数量较少，性能相对较好。

当规模较大时，可以使用分治法来改进算法，该算法的时间复杂度更优。算法的思路如下：

1. 将点按照横坐标从小到大排序。
2. 将点集分成左右两部分，并分别在这两个子集上递归调用自身来找到左右两边的最近点对。
3. 在递归的每一层，比较左分区的最近点对和右分区的最近点对，选择其中的最小距离，得到一个候选的最近点对和最小距离。
   然后考虑跨越左右两个分区的点对，计算它们之间的距离。如果跨越点对的距离小于已知的最小距离，则更新最小距离和最近点对。
4. 最后，返回三个距离中最小的值对应的点对，以及它们之间的最小距离。这样，就能够找到整个点集中的最近点对。

算法的关键思想是通过递归将问题分解成较小的子问题，然后通过合并子问题的结果来解决原始问题。

时间复杂度

1. 预处理排序步骤：首先，对点集按照横坐标排序的时间复杂度为 O(n log n)，这是常见的排序算法（如快速排序或归并排序）的时间复杂度。
2. 递归部分：递归调用 ClosestPair 函数时，每次都将点集分成两个子集，并进行递归调用。每个递归层级需要对一半的点集进行处理，所以总共有 O(log n) 层递归。在每一层递归中，需要进行一些常数时间的计算（如计算最近点对），因此递归部分的时间复杂度为 O(log n)。
3. 横跨两个分区的计算：在算法中，当满足条件横坐标距离(leftClosestPair, rightClosestPair) < minDistance 时，才会计算跨越两个分区的最近点对。这个计算的时间复杂度可以看作是线性的，因为在窄带区域内只需要考虑一些点对。这个部分的时间复杂度是 O(n)。

综上所述，该算法的时间复杂度由预处理排序步骤（O(n log n)）和递归部分（O(log n)）组成，其中递归部分的主要计算开销在于跨越两个分区的计算（O(n)）。因此，总体时间复杂度为：

\[O(n log_2n) \]

因此，改进算法的时间复杂度比暴力搜索的算法要好，因为它以对数方式增长，而不是二次方式增长。

伪代码

Algorithm ClosestPair(points)
    Input: 一个点集 points，包含 n 个点按横坐标排序
    Output: 最近的点对 closestPair 和它们之间的距离 minDistance

	// 也是递归出口
    If n <= 3 then
        Return BruteForceClosestPair(points)
    Else
    	// 按照横坐标排序
   		SortPointsByX(points)
    
        // 将 points 分成左右两部分 leftPoints 和 rightPoints
        leftClosestPair, leftMinDistance = ClosestPair(leftPoints)  // 递归调用左分区
        rightClosestPair, rightMinDistance = ClosestPair(rightPoints)  // 递归调用右分区

        minDistance = min(leftMinDistance, rightMinDistance)
        IF 横坐标距离(leftClosestPair, rightClosestPair) < minDistance then
            计算左右两部分之间的最近点对 stripClosestPair 和 stripMinDistance
        EndIf

        IF stripMinDistance < minDistance then
            Return stripClosestPair, stripMinDistance
        Else
            Return 最小的 minDistance 对应的 closestPair
        EndIf
    EndIf
End Algorithm

证明正确性

要证明该算法的正确性，可以使用分治法和归纳法。

基本情况：即 n <= 3 时的情况。在这种情况下，算法直接调用 BruteForceClosestPair(points) 来计算最近的点对。

归纳假设：假设 BruteForceClosestPair(points) 是正确的，因为它会考虑所有可能的点对并返回最近的点对及其距离。因此，在基本情况下，算法是正确的。

接下来，考虑递归情况，即 n > 3 的情况。在这种情况下，算法将点集分成左右两部分 leftPoints 和 rightPoints，然后递归地调用 ClosestPair(leftPoints) 和 ClosestPair(rightPoints) 来计算左右两个分区的最近点对和最小距离。

假设在递归调用中，ClosestPair(leftPoints) 和 ClosestPair(rightPoints) 都返回了正确的结果。现在需要证明合并这些结果时，算法仍然能够得到正确的结果。

算法比较了左右两个分区的最小距离 minDistance，然后计算了 stripClosestPair 和 stripMinDistance，它们是分布在左右两个分区之间的点对的最近距离。算法会选择其中较小的一个，并将其作为 minDistance。

然后，算法比较了 stripMinDistance 与 minDistance，如果 stripMinDistance 更小，那么算法返回 stripClosestPair 和 stripMinDistance，否则返回 minDistance 对应的最近点对。这确保了算法在任何情况下都返回正确的结果。

综上所述，算法在基本情况下和递归情况下都假设是正确的，然后通过合并左右两个分区的结果，选择最小距离的点对，确保了算法在任何情况下都返回正确的结果。因此，算法是正确的。

Question Number 3

Given an integer n, where 100 < n < 10000, please design an efficient algorithm to calculate 3^n , with a time complexity not exceeding O(n).

(a) Implement a naive calculation method to compute 3^n and analyze the time complexity of the naive calculation method.

(b) Propose an improved algorithm to calculate 3^n with a time complexity not exceeding O(n). Describe the algorithm’s concept and analyze its time complexity

(a)Native method

思路

1. 初始化一个变量 result 为 1，用于保存计算的结果。
2. 使用一个循环，循环 n 次，每次将 result 与 3 相乘，并将结果赋值给 result。
3. 循环结束后，result 中保存的就是 3^n 的计算结果。

时间复杂度

使用一个循环进行 n 次乘法操作来计算 3^n。每次乘法操作需要常数时间，因此循环中的操作的时间复杂度为 O(1)。

循环执行了 n 次，所以总的时间复杂度为 ：

\[O(n) \]

代码

由于该代码较容易实现，因此直接写出了具体java代码：

public static int calculatePower(int n) {
        int result = 1;
        for (int i = 0; i < n; i++) {
            result *= 3;
        }
        return result;
}

证明正确性

基本情况：，当 n 等于 0 时，方法返回 1。这是显然正确的，因为任何数的 0 次方都等于 1。

归纳假设：假设对于任意非负整数 k，calculatePower(k) 方法都能正确计算 3 的 k 次方。即，calculatePower(k) 返回的结果等于 3 的 k 次方。

现在考虑 n = k + 1 的情况。根据方法的实现，calculatePower(n) 的计算过程如下：

int result = 1;
for (int i = 0; i < n; i++) {
    result *= 3;
}

在循环中，result 初始值为 1，并且在每次迭代中都乘以 3。因此，循环结束后的 result 的值等于 3 的 n 次方。

根据归纳假设，calculatePower(k) 返回的结果等于 3 的 k 次方。而在 n = k + 1 的情况下，方法返回的结果等于 3 的 n 次方。因此，方法对于任意非负整数 n 都能正确计算 3 的 n 次方。

综上所述，calculatePower 方法是正确的，它能够正确计算 3 的任意非负整数次方。

(b)Improved algorithm

思路

在native method中，不断重复计算了之前已经计算过的数值，例如求3^{10,当算出3}5时，就无需计算

改进的算法可以使用递归和动态规划的思想，以降低时间复杂度。其主要思路如下：

1. 如果 n 是偶数，可以将问题分解为计算

   \[3^{\left(\frac{n}{2}\right)} * 3^{\left(\frac{n}{2}\right)} \]

   这可以通过计算 3^(n/2) 一次，然后平方得到结果。

2. 如果 n 是奇数，可以将问题分解为计算

   \[3^{\left(\frac{n-1}{2}\right)} * 3^{\left(\frac{n-1}{2}\right)} * 3 \]

   这可以通过计算 3^((n-1)/2) 一次，然后平方得到结果，再乘以 3。

3. 为了降低计算的复杂度，可以使用动态规划的方法，将已经计算过的 3^k 存储起来，以便后续使用。

时间复杂度

1. 对于每个不同的 n值，只计算一次，并将结果存储在 dp[] 数组中。这一步的时间复杂度是 O(n)。

2. 在递归部分，将问题分解为子问题，并计算这些子问题。
   假设 n 的二进制表示有 k 位（即 n 是 2 的 k 次方），那么最多会有 k 层递归。每一层递归的计算都涉及到常数次的乘法和除法操作，因此每一层递归的时间复杂度是 O(1)。

3. 综合考虑所有层次的递归，总的时间复杂度是 O(k)。由于 n是 2 的 k次方，因此 k与 log(n) 成正比。

   因此，这个算法的时间复杂度为：

\[O(log_2n) \]

代码

由于该代码较容易实现，因此直接写出了具体java代码：

public class CalculatePowerOfThree {
    private static int[] dp;  // 用于存储已计算的 3^k 值

    public static int calculatePower(int n) {
        dp = new int[n + 1];  // 初始化 dp 数组，用于存储计算结果
        return calculatePowerRecursive(n);
    }

    private static int calculatePowerRecursive(int n) {
        if (n == 0) {
            return 1;  // 3^0 = 1,递归出口
        }
        
        if (dp[n] != 0) {
            return dp[n];  // 如果已经计算过，直接返回结果
        }
        
        int result;
        if (n % 2 == 0) {
            int halfPower = calculatePowerRecursive(n / 2);
            result = halfPower * halfPower;
        } else {
            int halfPower = calculatePowerRecursive((n - 1) / 2);
            result = halfPower * halfPower * 3;
        }
        
        dp[n] = result;  // 将计算结果存储到 dp 数组中
        return result;
    }
}

证明正确性

为了证明该算法的正确性，可以使用数学归纳法。

基本情况：即 n=0 时算法的正确性。在这种情况下，calculatePowerRecursive(0) 应该返回 1，这是因为 3^0 等于 1。因此，基本情况成立。

归纳假设：假设对于任意 k，当 n=k 时算法的结果是正确的，即 calculatePowerRecursive(k) 返回的结果是 3^k。需要证明当 n=k+1 时算法仍然正确。

考虑 n=k+1 的情况，根据算法的递归步骤，如果 n是奇数，算法会计算 calculatePowerRecursive((n-1)/2) 并将其平方，再乘以 3。根据的归纳假设，calculatePowerRecursive((n-1)/2) 正确地返回了 3^((k+1-1)/2) = 3^k，所以平方后得到 3^(k+1)。然后再乘以 3，得到 3^(k+1+1) = 3^(k+2)，这正是期望的结果。

同样，如果 n 是偶数，算法会计算 calculatePowerRecursive(n/2) 并将其平方，得到 3^k。这也是期望的结果。

综上所述，使用数学归纳法证明了对于任意 n，算法 calculatePowerRecursive(n) 返回的结果是 3^n，因此证明了该算法的正确性。

Question Number 4

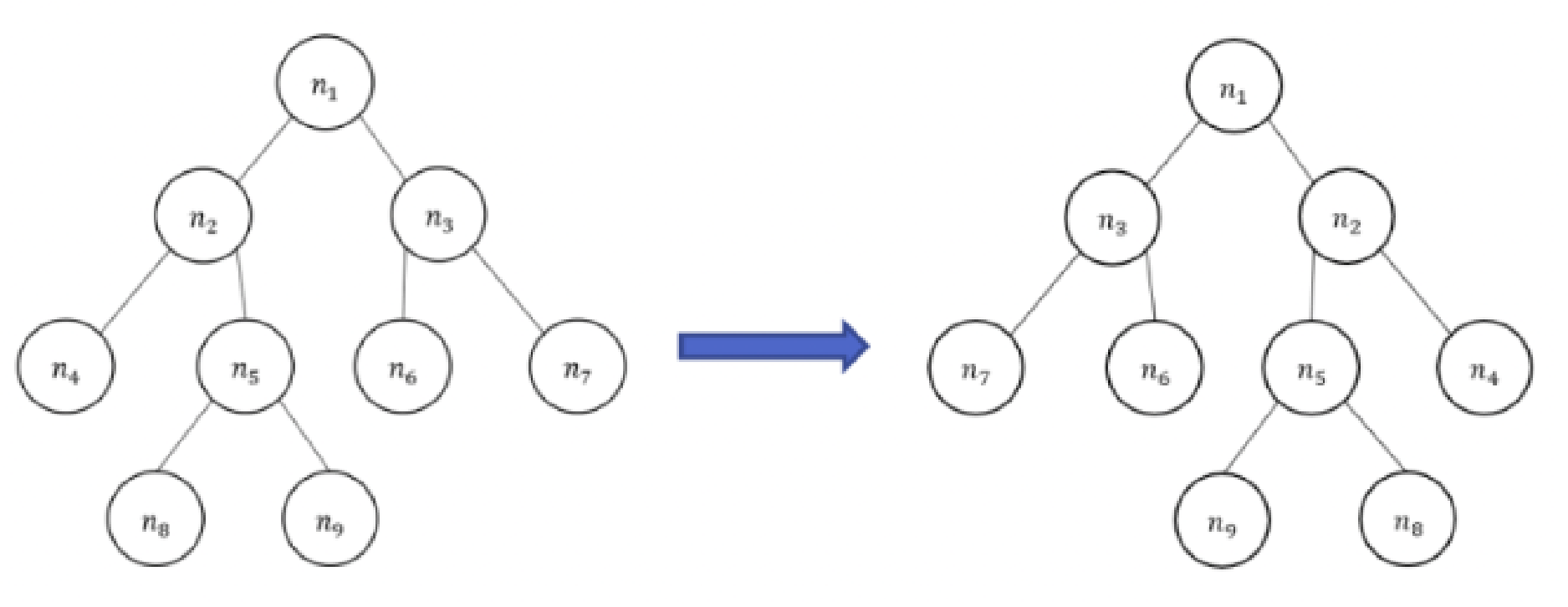
Given a binary tree T, please give an O(n) algorithm to invert binary tree. For example below, inverting the left binary tree, we get the right binary tree.

思路

1. 如果输入的二叉树根节点 root 为空，表示已经到达叶节点或空树，直接返回 null，作为递归的出口。
2. 否则，递归处理左子树和右子树。首先递归调用 invertTree 函数来翻转左子树，并将返回值赋给 root.left，这一步会一直递归到左子树的叶节点，然后开始回溯，逐级翻转左子树节点的左右子节点。
3. 同样地，递归调用 invertTree 函数来翻转右子树，并将返回值赋给 root.right，也是逐级递归和回溯。
4. 最后，交换 root 节点的左右子节点，完成翻转操作。
5. 返回根节点 root，表示整棵树已经完成翻转。

这个递归过程会从根节点开始，递归处理每个子树的左右子节点，直到叶节点，然后逐级回溯完成翻转操作。

时间复杂度

1. 根据递归的出口条件，如果输入的根节点 root 为空，返回 null，这一步的时间复杂度是 O(1)，因为只是一次条件判断和返回操作。
2. 对左子树的递归调用 invertTree(root.left) 和对右子树的递归调用 invertTree(root.right)，每次递归都是对子树进行操作，而且只进行了一次递归。因此，每次递归的时间复杂度是 O(1)。
3. 交换 root 节点的左右子节点的操作，包括将左子节点赋给右子节点，右子节点赋给左子节点，以及将临时节点的值赋给其中一个子节点。这些操作都是常数时间复杂度的操作，因此时间复杂度是 O(1)。

总结起来，整个算法的时间复杂度是 O(n)，因为在每个节点上都进行了一次递归操作，而递归的次数等于二叉树中的节点数 n。因此，时间复杂度是线性的，与二叉树的规模成正比。

代码

代码的实现较为简单，因此直接写出了java的具体实现

public TreeNode invertTree(TreeNode root) {
    if (root==null) return null;//递归出口
    root.left=invertTree(root.left);//一直递归左子树到叶节点，然后回溯，并用节点保持当前节点
    root.right=invertTree(root.right);//一直递归右子树到叶节点，然后回溯，并用节点保持当前节点

    TreeNode temp=root.left;//交换左右节点
    root.left=root.right;
    root.right=temp;
    return root;//返回当前要交换的节点
}

证明正确性

1. 如果一棵二叉树为空树，那么它的镜像也是空树，所以基本情况下是正确的。
2. 对于任意一个非空的二叉树，可以递归地交换它的左右子树，并且对左子树和右子树分别进行相同的操作。这个过程可以保持树的结构不变，只是交换了每个节点的左右子节点。因此，如果对左子树和右子树都正确地进行了翻转，那么整个树也就正确地完成了翻转。

基于以上，可以使用数学归纳法来证明算法的正确性：

基本情况： 当输入的二叉树为空树时，算法直接返回空树，这是正确的。

归纳假设：假设对于任意一棵高度为 h 的二叉树，算法能够正确地翻转。

现在考虑一棵高度为 h+1 的二叉树。这棵树可以看作是一个根节点和两棵子树的组合，其中左子树和右子树的高度都是 h。根据归纳假设，知道左子树和右子树都可以正确地翻转。那么只需要将根节点的左右子节点交换，就可以得到整棵高度为 h+1 的二叉树的翻转。

通过数学归纳法，证明了对于任意一棵二叉树，该算法能够正确地完成翻转。

Question Number 5

There are N rooms in a prison, one for each prisoner, and there are M religions, and each prisoner will follow one of them. If the prisoners in the adjacent room are of the same religion, escape may occur. Please give an O(n) algorithm to find out how many states escape can occur. For example, there are 3 rooms and 2 kinds of religions, then 6 different states escape will occur.

思路

因为只有相邻的信仰不相同才不能越狱，所以如果第一个房间有m种选择，

第二个房间保证与第一个房间不同即可，有m-1种选择

第三个房间保证与第二个房间不同即可，有m-1种选择

以此类推，所以得出公式，不可越狱方案数：

\[m * (m- 1 )^{n-1} \]

进入房间的总方案数为：

\[m^n \]

因此，可越狱的方案数为总方案数-不可越狱方案数：

\[m^n- (m * (m- 1 )^{n-1}) \]

但是传统的求幂方法计算量过大，因此可以使用快速幂算法来计算 M 的 N 次方和 (M-1) 的 N 次方，然后相减即可。

快速幂算法

快速幂算法的基本思想是将指数n表示为2进制形式，然后利用二进制形式中的位数来降低计算的复杂度。下面是该算法的基本步骤：

1. 将指数n表示为2进制形式，例如，n = 13可以表示为二进制数1101。
2. 从左到右遍历二进制表示的每一位，对于每一位i（从最高位到最低位），执行以下操作：
   • 如果当前位是1，就将底数a自乘a。这相当于将底数累乘多次。
   • 然后将底数a自乘自己（即a *= a），这相当于将底数平方。
3. 继续遍历下一位，重复第2步，直到遍历完所有位。
4. 当遍历完所有位时，底数a的值就等于指数n的幂，即a^n。

时间复杂度

这个算法的时间复杂度主要由两部分组成：

1. 计算 M 的 N 次方：这部分的时间复杂度由 fastExponentiation 函数决定。在 fastExponentiation 函数中，使用了迭代的方式计算幂运算，每次迭代将指数 exponent 除以 2，因此迭代次数最多为 log₂(N)，其中 N 表示指数。每次迭代中，进行一次乘法操作，因此总的时间复杂度为 O(log₂(N))。
2. 计算 (M-1) 的 N 次方：同样，这部分的时间复杂度也由 fastExponentiation 函数决定。因为在此计算的是 (M-1) 的 N 次方，所以在 fastExponentiation 函数中的指数仍然为 N。因此，这部分的时间复杂度也是 O(log₂(N))。

综上所述，算法的总时间复杂度是 O(log₂(N))，其中 N 表示宗教信仰的种类数量。

代码

public class PrisonEscapeStates {

    public static int countEscapeStates(int N, int M) {
        if (N <= 0 || M <= 0) {
            return 0;
        }

        // 计算总方案数
        int totalStates = fastExponentiation(M, N);
        // 计算不可越狱的方案数，使用快速幂
        int nonEscapeStates = fastExponentiation(M - 1, N - 1);
        // 可越狱的方案数等于总方案数减去不可越狱的方案数
        int escapeStates = totalStates - M*nonEscapeStates;
        return escapeStates;
    }

    // 快速幂算法
    private static int fastExponentiation(int base, int exponent) {
        int result = 1;
        while (exponent > 0) {
            if (exponent % 2 == 1) {
                result *= base;
            }
            base *= base;
            exponent >>= 1;
        }
        return result;
    }

    public static void main(String[] args) {
        int N = 3; // 3个房间
        int M = 2; // 2种宗教信仰
        int escapeStates = countEscapeStates(N, M);
        System.out.println("可越狱方案的数量为: " + escapeStates);
    }
}

验证正确性

首先，来分析 fastExponentiation 函数的正确性，通过数学归纳法证明。

假设 fastExponentiation(base, exponent) 正确计算 base 的 exponent 次方。现在考虑 fastExponentiation(base, exponent+1)，即计算 base 的 (exponent+1) 次方。根据快速幂算法的步骤，可以将 (exponent+1) 表示为二进制形式，例如 exponent+1 = b_k * 2^k + b_(k-1) * 2^(k-1) + ... + b_1 * 2 + b_0，其中 b_k, b_(k-1), ..., b_0 是二进制位。

根据步骤 2，当 b_0 为 1 时，将 base 乘以 result。根据步骤 3，将 base 自乘一次。因此，如果可以证明 fastExponentiation(base, exponent) 正确计算 base 的 exponent 次方，那么 fastExponentiation(base, exponent+1) 也会正确计算 base 的 (exponent+1) 次方。

已经证明了 fastExponentiation 函数的正确性。接下来，来证明 countEscapeStates 函数的正确性。

countEscapeStates 函数中，首先计算总方案数 totalStates，然后计算不可越狱的方案数 nonEscapeStates，最后通过总方案数减去不可越狱的方案数得到可越狱的方案数 escapeStates。这个过程与数学归纳法中的归纳步骤非常相似。

基础情况：当 N 为 1 时，即只有一个房间，不管有多少种宗教信仰，都没有相邻的房间，不可越狱的方案数为 0，而总方案数为 M。因此，计算结果是正确的。

归纳假设：假设对于任意 N，countEscapeStates 函数都能正确计算可越狱的方案数。现在考虑 N+1 的情况。可以将 N+1 个房间分成两部分，前 N 个房间和第 N+1 个房间。根据归纳假设，前 N 个房间的可越狱方案数是正确的。对于第 N+1 个房间，它可以选择任意一种宗教信仰，因此有 M 种选择。不可越狱的方案数等于前 N 个房间的不可越狱方案数乘以 M-1（因为第 N+1 个房间的宗教信仰不能与相邻房间相同），即 nonEscapeStates = (M-1) * nonEscapeStates_N，其中 nonEscapeStates_N 是前 N 个房间的不可越狱方案数。

因此，总方案数 totalStates 是正确的，不可越狱的方案数 nonEscapeStates 也是正确的，从而可越狱的方案数 escapeStates 也是正确的。

综上所述，通过数学归纳法证明了 countEscapeStates 函数的正确性。