数据结构与算法(3)
算法笔记3
一、图
public class Graph {
/**
* 顶点的list集合
*/
private ArrayList<String> vertexList;
/**
* 顶点对应的邻接矩阵
*/
private int [][] adjacencyMatrix;
/**
* 边的个数!
*/
private int edgeCount;
/**
* 顶点个数
*/
private int vertexCount;
public Graph(int vertexCount) {
this.vertexCount =vertexCount;
vertexList = new ArrayList<>(vertexCount);
adjacencyMatrix = new int[vertexCount][vertexCount];
edgeCount = 0;
}
/**
* 添加节点
*/
public void addVertex(String vertex){
if (vertexList.size() == vertexCount){
System.out.println("顶点数已满");
return;
}
vertexList.add(vertex);
}
/**
* 通过字符顶点,获取在临界矩阵中的数字顶点
* @param vertex
* @return
*/
public int getIntByVertex(String vertex){
int num = 0;
for (String s : vertexList) {
if (s == vertex){
break;
}
num++;
}
return num;
}
/**
* 添加边
*/
public void addEdge(String vertex1,String vertex2,int weight){
int vertexNum1 = getIntByVertex(vertex1);
int vertexNum2 = getIntByVertex(vertex2);
adjacencyMatrix[vertexNum1][vertexNum2] = weight;
adjacencyMatrix[vertexNum2][vertexNum1] = weight;
edgeCount++;
}
/**
* 展示
*/
public void showGraph(){
for (int[] rows : adjacencyMatrix) {
for (int vertex : rows) {
System.out.printf(vertex+" ");
}
System.out.println("");
}
}
/**
* 获取邻接节点
* @return
*/
public String getAdjacentNode(String s){
int intByVertex = getIntByVertex(s);
for (int i = 0; i < vertexCount; i++){
//如果有边,并且末节点为访问过
if (adjacencyMatrix[intByVertex][i] != 0&& isVisit[i] == false){
return getStrByInt(i);
}
}
return null;
}
}
1.1深度优先
/**
* DFS搜索
*/
public void DFSSearch(){
Stack<String> stack = new Stack<>();
//1.将第一个元素压入栈,并将访问情况至为true
//访问情况
isVisit[0] = true;
//搜索到元素,打印操作
System.out.printf(vertexList.get(0));
//压入栈
stack.push(vertexList.get(0));
//循环
while (stack.isEmpty() != true){
//获取栈顶元素的邻接节点
String adjacentNode = getAdjacentNode(stack.peek());
if (adjacentNode == null){
stack.pop();
}
else {
//访问情况
isVisit[getIntByVertex(adjacentNode)] = true;
//搜索到元素,打印操作
System.out.printf(adjacentNode);
//压入栈
stack.push(adjacentNode);
}
}
//还原
for (int i = 0; i < vertexCount; i++) {
isVisit[i] = false;
}
}
1.2广度优先
/**
* 广度优先搜索
*/
public void BFSSearch(){
ArrayQueue<String> queue = new ArrayQueue<String>(edgeCount);
//1.将第一个元素压入栈,并将访问情况至为true
//访问情况
isVisit[0] = true;
//搜索到元素,打印操作
System.out.printf(vertexList.get(0));
//压入栈
queue.add(vertexList.get(0));
String next;
while (queue.isEmpty() != true){
//对头出队列
String s = queue.remove(0);
while (( next = getAdjacentNode(s)) != null){
isVisit[getIntByVertex(next)] = true;
System.out.printf(next);
queue.add(next);
}
}
//还原
for (int i = 0; i < vertexCount; i++) {
isVisit[i] = false;
}
}
二、算法
2.1非递归二分查找
/**
* 非递归二分查找
* @param arr 查找数组
* @param target 目标元素
* @return 目标元素下标
*/
public static int binarySearchNoRecursion(int [] arr, int target){
int left = 0;
int right = arr.length - 1;
int mid = 0;
//当左边界小于右边界时,一直查找
while (left <= right){
//中值
mid = (left+right) / 2;
//找到
if (arr[mid] == target){
return mid;
}
//中值大于目标值
if (arr[mid] > target){
//向左寻找
right = mid - 1;
}
else
{
//向右
left = mid + 1;
}
}
//没找到
return -1;
}
2.2分治算法(汉罗塔问题)
/**
* 分治算法模仿 汉罗塔问题
* @param num 罗盘数
* @param a 第一个柱子
* @param b 第二个柱子
* @param c 第三个柱子
*/
public static void divideAndConquer(int num, String a,String b, String c){
if (num == 1){
System.out.println("第1个盘从" +a+ "->" +c);
}
//此时盘数大于1,将盘看做两个盘:
//第一个盘为上面所有盘, 第二个盘为最下面的盘
/*
分为三步:
1.把上面所有盘从a->b
2.把最下面的盘从a->c
3.把b的盘移到c
*/
else {
//1.把上面所有盘从a->b
divideAndConquer(num-1,a,c,b);
//2.把最下面的盘从a->c
System.out.println("第"+num+"个盘从"+a+"->"+c);
//3.把b的盘移到c
divideAndConquer(num-1,b,a,c);
}
}
2.3动态规划
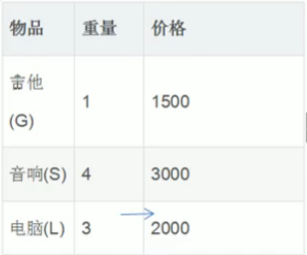
问:背包总称重4,物品不重复的前提,如何保证背包装的价格最高
/**
* @Author: 郜宇博
* @Date: 2021/8/11 15:31
* 动态规划问题
*/
public class DynamicProgramming {
public static void main(String[] args) {
int []weight = {1,4,3};
int []value = {1500,3000,2000};
int knapsackWeight = 4;
knapsackProblem(weight,value,knapsackWeight);
}
public static void knapsackProblem(int[] weight,int[] value, int knapsackWeight){
//物品数量
int G,S,L = 0;
//用于存储各重量背包价值
int [][] knapsackValue = new int[weight.length+1][knapsackWeight+1];
int [][] path = new int[weight.length+1][knapsackWeight+1];
//第一行和第一列设为0
for (int i =0; i < knapsackValue.length; i++){
knapsackValue[i][0] = 0;
}
for (int i =0; i < knapsackValue[0].length; i++){
knapsackValue[0][i] = 0;
}
//动态规划
for (int i = 1; i < knapsackValue.length; i++){
for (int j = 1; j < knapsackValue[i].length; j++){
if (weight[i-1]>j){
//物品大于背包重量
knapsackValue[i][j] = knapsackValue[i-1][j];
}
else {
//如果放入背包
if ((value[i-1]+knapsackValue[i-1][j-weight[i-1]]) > knapsackValue[i-1][j]){
knapsackValue[i][j] = value[i-1]+knapsackValue[i-1][j-weight[i-1]];
//是否到达最后一个点
path[i][j] = 1;
}
//如果不放入背包
else {
knapsackValue[i][j] = knapsackValue[i-1][j];
}
}
}
}
//展示
for (int[] ints : knapsackValue) {
for (int anInt : ints) {
System.out.printf(anInt+" ");
}
System.out.println("");
}
int i = path.length - 1;
int j = path[0].length - 1;
while (i>0&&j>0){
if (path[i][j] == 1){
System.out.println("第"+i+"个商品放到背包");
j = j- weight[i-1];
}
i--;
}
}
}


