数据挖掘算法——C4.5决策树算法
参考博客:
https://www.jianshu.com/p/8eaeab891341 (C4.5)
决策树是一种逼近离散值目标函数的方法,学习到的函数被表示为一棵决策树
根节点包含全部训练样本 自顶向下分而治之的策略
决策树算法以树状结构来表示数据的分类结果,每一个决策点实现一个具有离散输出的测试函数,记为分支
根节点
非叶子节点 (代表测试的条件,对数据属性的测试 决策点)
叶子节点 (代表分类后所获得的分类标记)
分支 (代表测试的结果)
决策树-熵
P(X,Y) = P(X) * P(Y) X和Y两个事件相互独立 Log(XY) = Log(X) + Log(Y)
H(X),H(Y)当成它们发生的不确定性
P(几率越大)->H(X)值越小 如:今天正常上课
P(几率越小)->H(X)值越大 如:今天没翻车
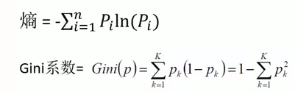
我们统计了14天的气象数据(指标包括outlook,temperature,humidity,windy),并已知这些天气是否打球(play)。如果给出新一天的气象指标数据:sunny,cool,high,TRUE,判断一下会不会去打球。
table 1
| outlook | temperature | humidity | windy | play |
| sunny | hot | high | FALSE | no |
| sunny | hot | high | TRUE | no |
| overcast | hot | high | FALSE | yes |
| rainy | mild | high | FALSE | yes |
| rainy | cool | normal | FALSE | yes |
| rainy | cool | normal | TRUE | no |
| overcast | cool | normal | TRUE | yes |
| sunny | mild | high | FALSE | no |
| sunny | cool | normal | FALSE | yes |
| rainy | mild | normal | FALSE | yes |
| sunny | mild | normal | TRUE | yes |
| overcast | mild | high | TRUE | yes |
| overcast | hot | normal | FALSE | yes |
| rainy | mild | high | TRUE | no |
这个问题当然可以用朴素贝叶斯法求解,分别计算在给定天气条件下打球和不打球的概率,选概率大者作为推测结果。
现在我们使用ID3归纳决策树的方法来求解该问题。
预备知识:信息熵
熵是无序性(或不确定性)的度量指标。假如事件A的全概率划分是(A1,A2,...,An),每部分发生的概率是(p1,p2,...,pn),那信息熵定义为:

通常以2为底数,所以信息熵的单位是bit。
补充两个对数去处公式:

ID3算法
构造树的基本想法是随着树深度的增加,节点的熵迅速地降低。熵降低的速度越快越好,这样我们有望得到一棵高度最矮的决策树。
在没有给定任何天气信息时,根据历史数据,我们只知道新的一天打球的概率是9/14,不打的概率是5/14。此时的熵为:

属性有4个:outlook,temperature,humidity,windy。我们首先要决定哪个属性作树的根节点。
对每项指标分别统计:在不同的取值下打球和不打球的次数。
table 2
| outlook | temperature | humidity | windy | play | |||||||||
| yes | no | yes | no | yes | no | yes | no | yes | no | ||||
| sunny | 2 | 3 | hot | 2 | 2 | high | 3 | 4 | FALSE | 6 | 2 | 9 | 5 |
| overcast | 4 | 0 | mild | 4 | 2 | normal | 6 | 1 | TRUR | 3 | 3 | ||
| rainy | 3 | 2 | cool | 3 | 1 | |
|||||||
下面我们计算当已知变量outlook的值时,信息熵为多少。
outlook=sunny时,2/5的概率打球,3/5的概率不打球。entropy=0.971
outlook=overcast时,entropy=0
outlook=rainy时,entropy=0.971
而根据历史统计数据,outlook取值为sunny、overcast、rainy的概率分别是5/14、4/14、5/14,所以当已知变量outlook的值时,信息熵为:5/14 × 0.971 + 4/14 × 0 + 5/14 × 0.971 = 0.693
这样的话系统熵就从0.940下降到了0.693,信息增溢gain(outlook)为0.940-0.693=0.247
同样可以计算出gain(temperature)=0.029,gain(humidity)=0.152,gain(windy)=0.048。
gain(outlook)最大(即outlook在第一步使系统的信息熵下降得最快),所以决策树的根节点就取outlook。

接下来要确定N1取temperature、humidity还是windy?在已知outlook=sunny的情况,根据历史数据,我们作出类似table 2的一张表,分别计算gain(temperature)、gain(humidity)和gain(windy),选最大者为N1。
依此类推,构造决策树。当系统的信息熵降为0时,就没有必要再往下构造决策树了,此时叶子节点都是纯的--这是理想情况。最坏的情况下,决策树的高度为属性(决策变量)的个数,叶子节点不纯(这意味着我们要以一定的概率来作出决策)。
概要
- 关于决策树
决策树其实是一种分类算法,目标是将具有P个维度特征的样本n划分到c个类别中: c = f(n); 通过这种分类的过程表示为一棵树,每次通过选择一个特征pi来进行分叉。
每个叶节点对应着一个分类,非叶节点对应着在每个属性上的划分,根据样本在该属性上的不同取值将其划分成若干个子集。对于非纯的叶节点,多数类的标号给出到达这个节点的样本所属的类。
构建决策树的核心问题: 在每一步如何选择适当的属性对样本进行拆分。
- 不同的决策树算法有着不同的特征选择方案
1、ID3: 信息增益
2、C4.5: 信息增益率
3、CART: gini系数(基尼系数)
| 算法 | 描述 | 适用 |
|---|---|---|
| ID3 | 在决策树的各级节点上,使用信息增益方法作为属性选择标准,来确定生成每个节点时所采用的合适属性 | 适用于离散的描述属性 |
| C4.5 | 使用信息增益率来选择节点属性,并克服ID3算法的不足 | 即适用离散的描述属性呦适用连续的描述属性 |
| CART | 是一种有效的非参数分类和回归方法,通过构建树、修建树、评估树来构建二叉树 | 当终结点为连续属性时该树为回归树;当终节点为分类变量时,即为分类树 |
实例

数据总结: 属性数据4个 = {天气,温度,湿度,风速}
类别2个 = {进行,取消}
1、类型信息熵
定义:所有样本中各种类别出现的不确定性之和,根据熵的概念,熵越大,不确定性就越大。需要研究清楚信息就越多。

2、每个属性的信息熵
每个属性信息熵相当于一种条件熵。表示在某种属性的条件下,各种类别出现的不确定性之和。属性的信息熵越大,该属性拥有的样本类型越不“纯”。

3、信息增益
信息增益 = 熵 - 条件熵(信息类别熵 - 属性信息熵);表示信息不确定性减少的程度。若是一个属性的信息增益越大,就表示用这个属性进行样本划分可以更好的减少划分后样本的不确定性。当然,选择该属性就可以更快更好的完成分类目标。
信息增益的ID3算法的特征选择指标

4.属性分裂信息度量
通过分裂信息度量来考虑某种属性进行分裂时分支的数量信息和尺寸信息,而这些信息称之为属性的内在信息。
信息增益率 = 信息增益 / 内存信息,导致属性的重要性随内在信息的增大而减小(换句话说:若是某个属性本身的不确定性很大,那就不倾向选取它)。是对单纯使用信息增益有所补偿

5、信息增益率
IGR(天气) = Gain(天气) / H(天气) = 0.246 / 1.577 = 0.155
IGR(温度) = Gain(温度) / H(温度) = 0.029 / 1.556 = 0.0186
IGR(湿度) = Gain(湿度) / H(湿度) = 0.151 / 1.0 = 0.151
IGR(风速) = Gain(风速) / H(风速) = 0.048 / 0.985 = 0.048

结论

后续
信息熵:体现的是在整个样本数据集中,结果类型或条件属性在对应的结果集中单一事件出现不确定性的概率;而这个不确定性的结果和对应的结果类型或条件属性存在log的联系;信息的不确定性越大,熵的值也就越大; 针对的是一元模型的概率
-(同一结果类型记录的个数) / (整个样本数据结果类型记录的总数) * log2((同一结果类型记录的个数) / (整个样本数据结果类型记录的总数))
条件熵: 通过多元模型的方式来减少一元模型中不确定性,或者说降低对应的熵,越低意味着信息的不确定性就越小。
条件熵 = -某个条件属性某个类型/总结果记录数 * 该条件属性某个类型的不同细分类的信息熵 之和
该条件属性某个类型的不同细分类的信息熵 = 同个属性不同内容类型相对结果类型的信息熵的之和



 浙公网安备 33010602011771号
浙公网安备 33010602011771号